Difference between revisions of "Relativistic Frames of Reference"
Jump to navigation
Jump to search
| Line 42: | Line 42: | ||
<center><math>c=3\times 10^8\ m/s</math></center> | <center><math>c=3\times 10^8\ m/s</math></center> | ||
| − | Using the distance equation in a Cartesian coordinate system, the | + | Using the distance equation in a Cartesian coordinate system, the equation for the speed of light becomes |
| Line 48: | Line 48: | ||
| + | Following the postulate of Special Relativity, this implies for the primed frame | ||
| + | |||
| + | |||
| + | <center><math>c=\frac{\sqrt{(\Delta x')^2+(\Delta y')^2+(\Delta z')^2}}{\Delta t'}</math></center> | ||
| + | |||
| + | We can rewrite this as | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>c^2=\frac{(\Delta x')^2+(\Delta y')^2+(\Delta z')^2}{(\Delta t')^2}</math></center> | ||
---- | ---- | ||
Revision as of 03:20, 3 June 2017
Relativistic Frames of Reference
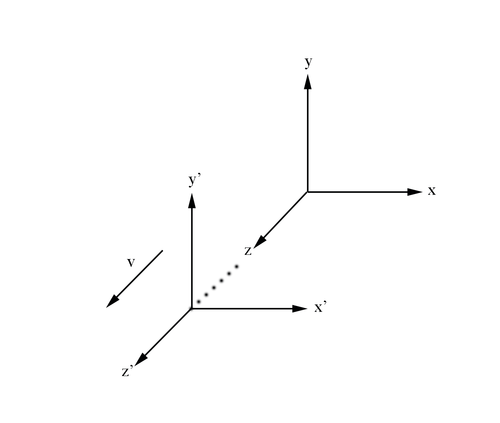
From the Galilean description of motion for a frame of reference moving relative to another frame considered stationary we know that
Using Einstein's Theory of Relativity, we know that the speed of light is a constant, c, for all reference frames. In the unprimed frame, from the definition of speed:
where
Using the distance equation in a Cartesian coordinate system, the equation for the speed of light becomes
Following the postulate of Special Relativity, this implies for the primed frame
We can rewrite this as