|
|
| Line 59: |
Line 59: |
| | | | |
| | | | |
| − | <center><math>\frac{x_{n=1}}{sin 4.79^{\circ}}=\frac{2.52934}{sin 110.21^{\circ}} \Rightarrow x_{n=1}=.2252</math></center> | + | <center><math>\frac{x_{n=1}}{sin 5.20988^{\circ}}=\frac{2.52934}{sin 109.79^{\circ}} \Rightarrow x_{n=1}=.2441</math></center> |
| | | | |
| | | | |
| Line 66: |
Line 66: |
| | | | |
| | | | |
| − | <center><math>.2252-.01337=.2117=x_{n=0}</math></center> | + | <center><math>.2441-.01337=.2307=x_{n=0}</math></center> |
| | | | |
| | | | |
| | Each wire becomes an equation of the form, | | Each wire becomes an equation of the form, |
| | | | |
| − | <center><math>x_{wire\ n}'=tan(6^{\circ})y'+.2117+.01337\ n</math></center> | + | <center><math>x_{wire\ n}'=tan(6^{\circ})y'+.2307+.01337\ n</math></center> |
| | | | |
| | This agrees with CED simulation | | This agrees with CED simulation |
Revision as of 15:24, 7 March 2017
Function for the wire number in the detector frame for change in [math]\phi[/math] and constant [math]\theta[/math] in the lab frame
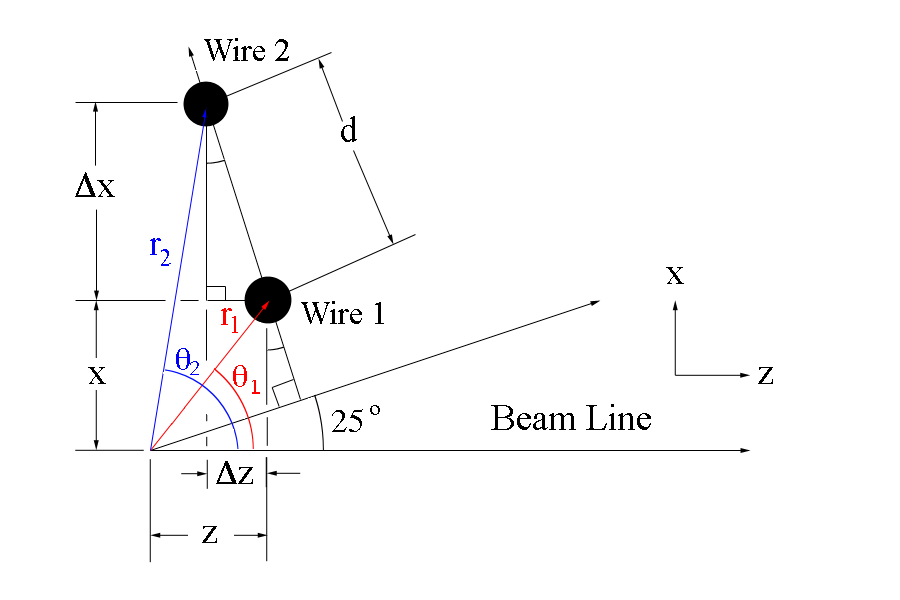
Using the expression for wire number n in terms of [math]\theta[/math] for the detector mid-plane where [math]\phi=0[/math]:
[math]n = \frac{-957.412}{\tan(\theta)+2.14437}+430.626[/math]
We can use the inverse of this function to find the neighboring wire's corresponding angle theta
[math]\theta\equiv 4.49876 +0.293001 n+0.000679074 n^2-3.57132\times 10^{-6} n^3[/math]
[math]\theta(n \pm 1)\equiv 4.49876 +0.293001 (n \pm 1)+0.000679074 (n \pm 1)^2-3.57132\times 10^{-6} (n \pm 1)^3[/math]
We also know what the x' function must follow dependent on phi in the detector plane
[math]x_1^'=\frac{((x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2)-((x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2)}{4ae}-ae[/math]
[math]x_1^'=\frac{(r_{D2}^2)-(r_{D1}^2)+cot^2(\theta)(r_{D2}^2-r_{D1}^2)-2x_P(x_{D2}-x_{D1})-2y_P(y_{D2}-y_{D1})-2z_P(z_{D2}-z_{D1})}{4ae}-ae[/math]
| [math]x_{D1}=r_{D1}\ cos(\phi)\qquad y_{D1}=r_{D1}cos(\phi)\qquad z_{D1}=r_{D1} cot(\theta)[/math]
|
| [math]x_{D2}=r_{D2} cos(\phi)\qquad y_{D2}=r_{D2} sin(\phi)\qquad z_{D2}=r_{D2} cot(\theta)[/math]
|
| [math]x_P=\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
| [math]y_P=\frac{2.53sin(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
| [math]z_P=\frac{2.53cot(\theta)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
[math]r_{D1}=R_{Lower\ Dandelin}cos(\theta)=(ae-\Delta a) tan(65^{\circ})cos(\theta)\qquad \qquad r_{D2}=R_{Lower\ Dandelin}cos(\theta)=(ae+\Delta a) tan(65^{\circ})cos(\theta)[/math]
We can take this point to be the x axis intercept and use the fact that each wire is titled by 6 degrees to the horizontal in the plane of the detector to create an equation
[math]x_{wire\ n}'=tan(6^{\circ})y'+x_{n_0}[/math]
where the initial wire and x' position at the given theta is represented by [math]n_0[/math]
This equation can be solved for a hypothetical wire 0, which will allow the wire number to be the multiplicative factor for the change from the starting position.
[math]\frac{x_{n=1}}{sin 5.20988^{\circ}}=\frac{2.52934}{sin 109.79^{\circ}} \Rightarrow x_{n=1}=.2441[/math]
Since each wire is separated by .01337 meters
[math].2441-.01337=.2307=x_{n=0}[/math]
Each wire becomes an equation of the form,
[math]x_{wire\ n}'=tan(6^{\circ})y'+.2307+.01337\ n[/math]
This agrees with CED simulation