Determining wire-phi correspondance

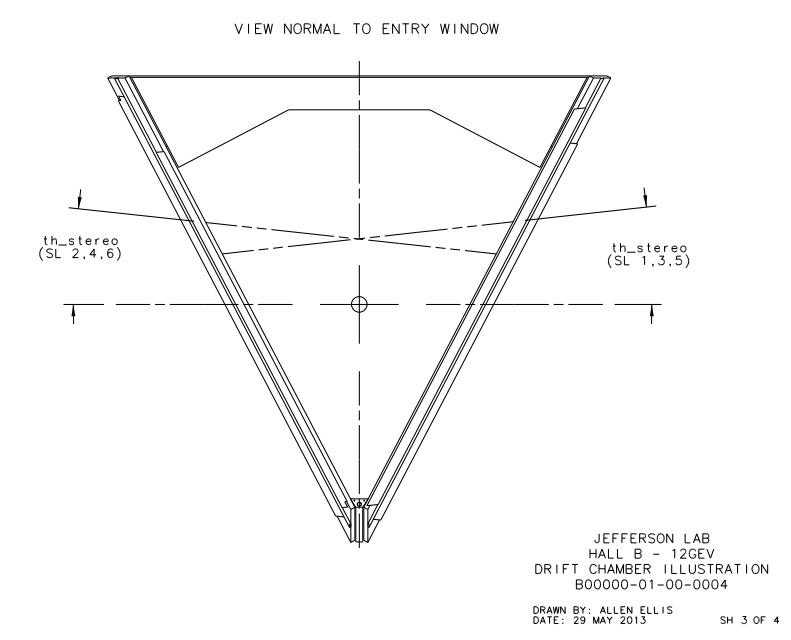
Examining the geometry of the Drift Chamber, we can see that the detector is similar to a hexagonal pyramid in shape.

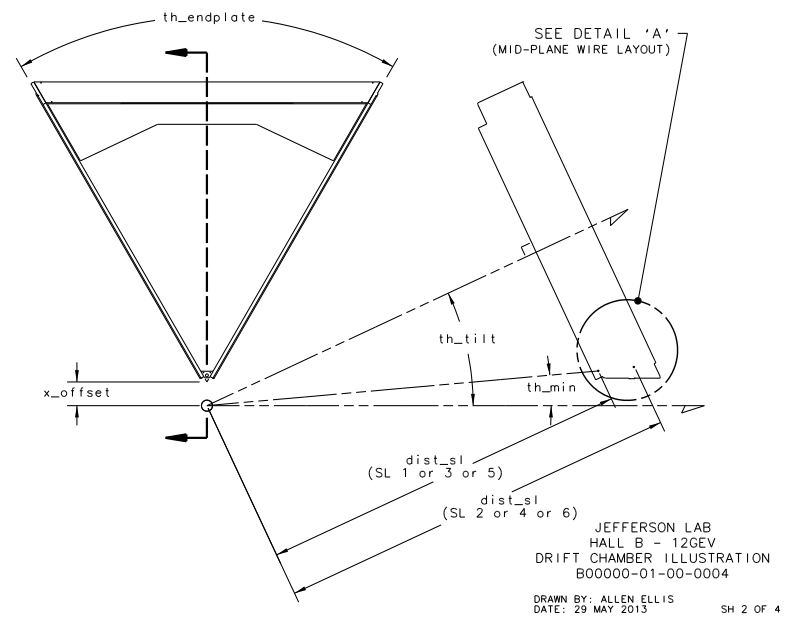
From the geometry it is given that xdist, the distance between the line of intersection of the two end-plate planes and the target position, is equal to 8.298 cm and th_min, the angle from the target vertex to the the same line, is 4.694 degrees. Using this knowledge we can simulate this situation by having the end-plate planes intersect at the beam line axis. This action in effect would grant the sector to measure angles below ~5 degrees, which we can account for by limiting angles theta within the accepted detector range. The quantity dist2tgt, the distance from the target to the first guard wire plane along the normal of said plane, is given as 228.078 cm. Using the previous understanding of the distances between planes within a Superlayer:

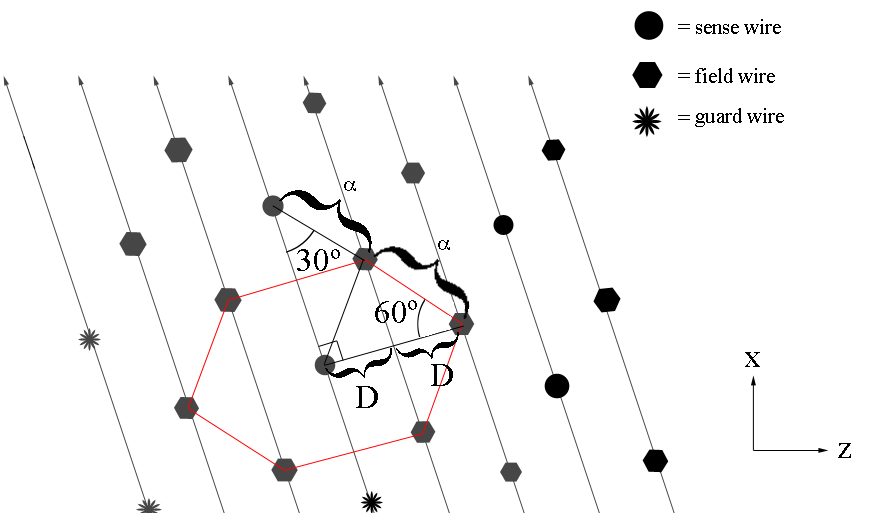
We know that the seperation between levels is a constant D=.3861 cm

This gives us the distance to level 1 from the vertex (0,0,0) as 228.078 cm+0.3861 cm=228.4641 cm in the positive z direction.

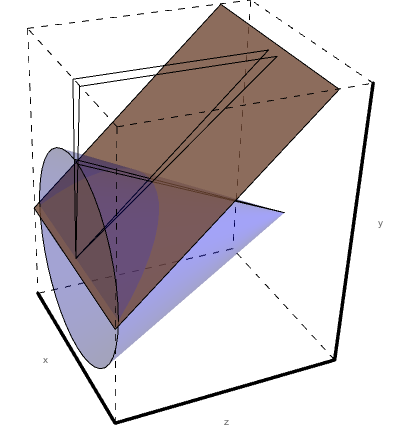
When the scattering angle theta, which is measured with respect to the beam line, is held constant and rotated through 360 degrees in phi, a cone is created. Using Mathematica, we can produce a 3D rendering of how the sectors for Level 1 would have to interact with a steady angle theta with respect to the beam line, as angle phi is rotated through 360 degrees.

Looking just at sector 1, we can see that the intersection of level 1 and the cone of constant angle theta forms a conic section.

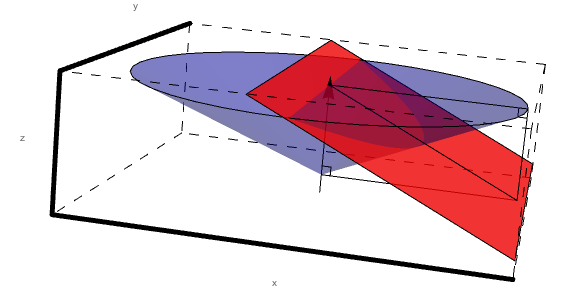
Following the rules of conic sections we know that the eccentricity of the conic is given by:

[math]e=\frac{\sin \beta}{\sin\alpha}[/math]

Where β is the angle of the plane, which in our case is 25 degrees for the sectors with respect to the beam line (axis of rotation of the cone).

This leaves α is the slant of the cone, which is the angle theta that the particle must be traveling with respect to the beamline.

If the conic is an circle, e=0

If the conic is an parabola, e=1

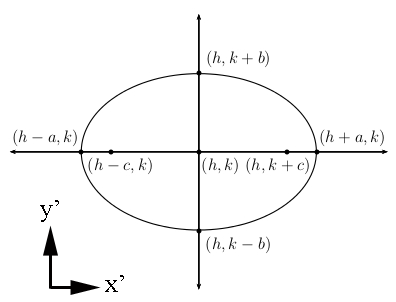
If the conic is an ellipse, [math]e=\sqrt{1-\frac{b^2}{a^2}}[/math]

For ellipses centered at (h,k):

[math]\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1[/math]

where

[math]a = major\ radius\ (= \frac{1}{2}\ length\ major\ axis)[/math]

[math]b = minor\ radius\ (= \frac{1}{2}\ length\ minor\ axis)[/math]

Where

[math]c^2=a^2-b^2[/math]

For a parabola:

[math]4px = y^2[/math]

where

p = distance from vertex to focus (or directrix)