Difference between revisions of "Determining wire-phi correspondance"
| Line 6: | Line 6: | ||
| − | xdist - distance between the line of intersection of the two end-plate planes and | + | xdist - distance between the line of intersection of the two end-plate planes and the target position =8.298 cm th_min=4.694 |
| − | the target position =8.298 cm | ||
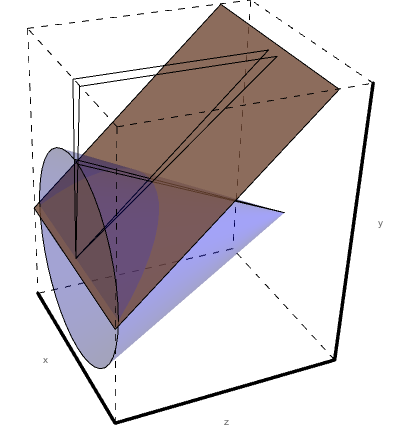
Using Mathematica, we can produce a 3D rendering of how the sectors for Level 1 would have to interact with a steady angle theta with respect to the beam line, as angle phi is rotated through 360 degrees. | Using Mathematica, we can produce a 3D rendering of how the sectors for Level 1 would have to interact with a steady angle theta with respect to the beam line, as angle phi is rotated through 360 degrees. | ||
Revision as of 16:41, 3 January 2017
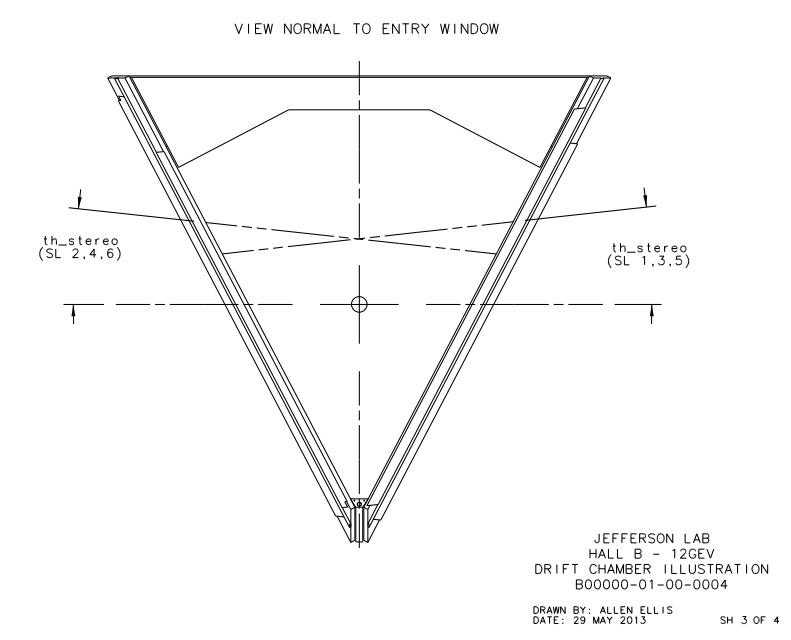
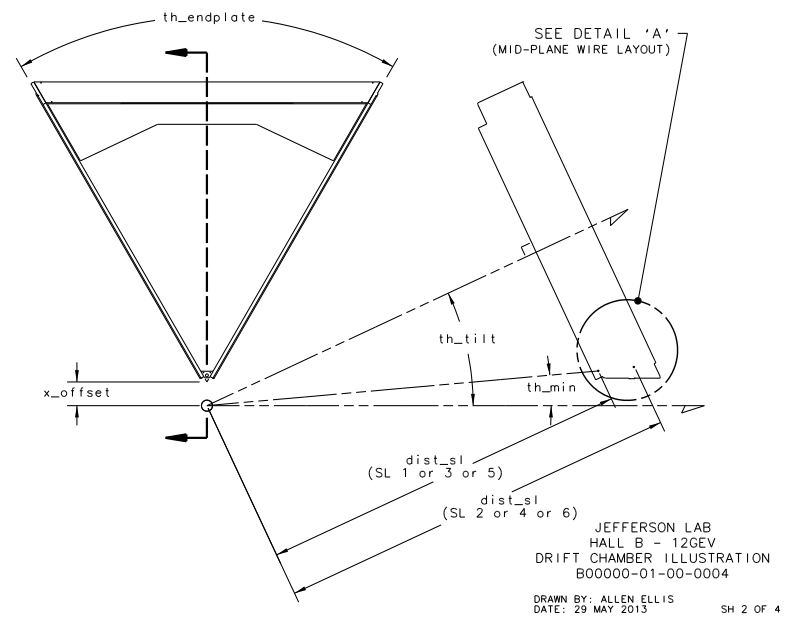
xdist - distance between the line of intersection of the two end-plate planes and the target position =8.298 cm th_min=4.694
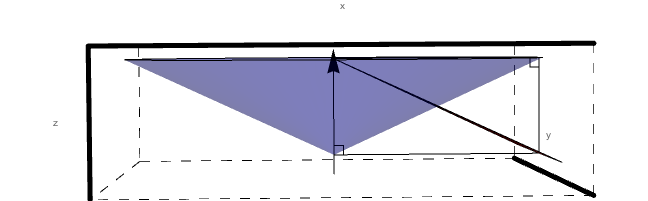
Using Mathematica, we can produce a 3D rendering of how the sectors for Level 1 would have to interact with a steady angle theta with respect to the beam line, as angle phi is rotated through 360 degrees.
Looking just at sector 1, we can see that the intersection of level 1 and the cone of constant angle theta forms a conic section.
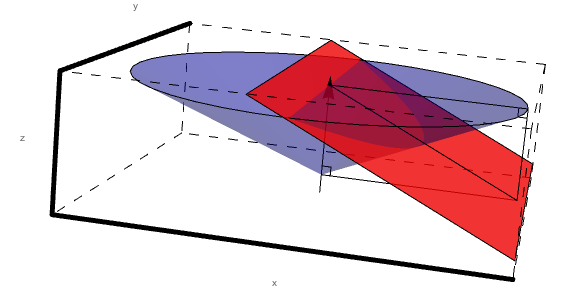
Following the rules of conic sections we know that the eccentricity of the conic is given by:
Where β is the angle of the plane, which in our case is 25 degrees for the sectors with respect to the beam line (axis of rotation of the cone).
This leaves α is the slant of the cone, which is the angle theta that the particle must be traveling with respect to the beamline.
If the conic is an circle, e=0
If the conic is an parabola, e=1
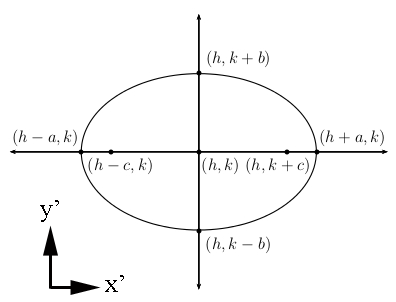
If the conic is an ellipse,
For ellipses centered at (h,k):
where
Where
For a parabola:
where
p = distance from vertex to focus (or directrix)