Determining wire-phi correspondance

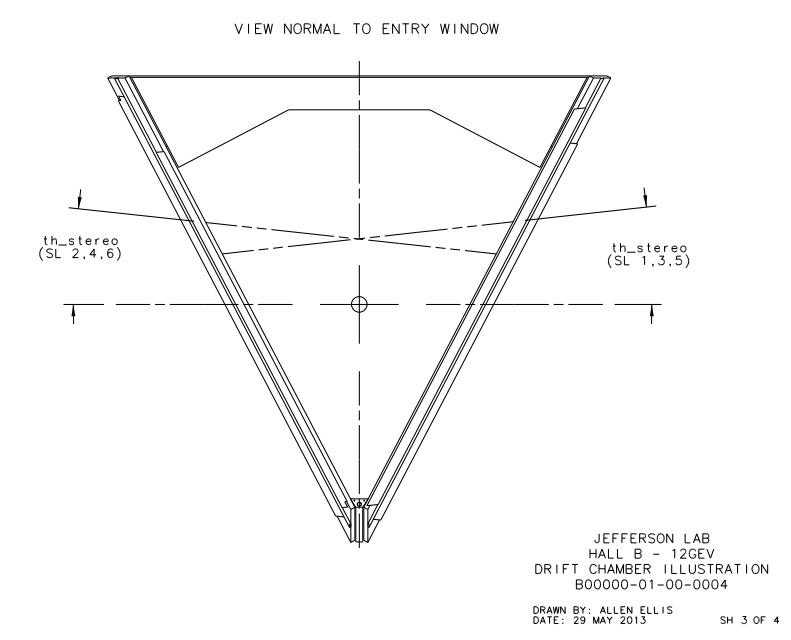
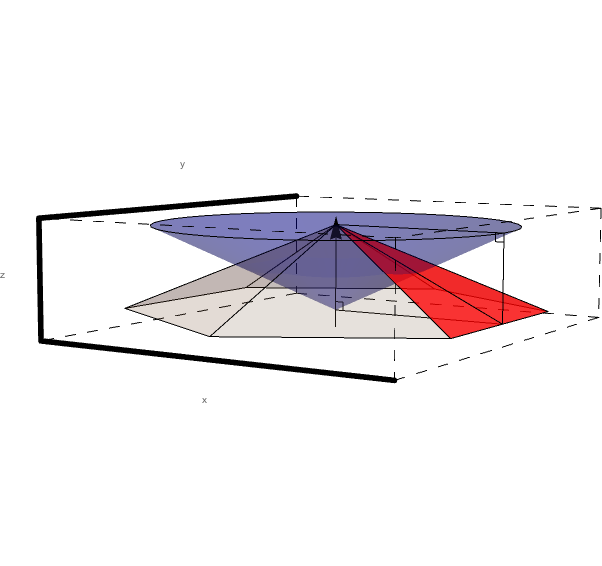
Using Mathematica, we can produce a 3D rendering of how the sectors for Level 1 would have to interact with a steady angle theta with respect to the beam line, as angle phi is rotated through 360 degrees.

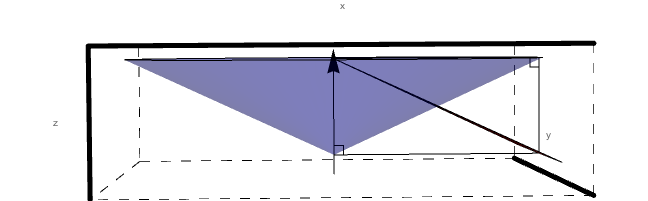
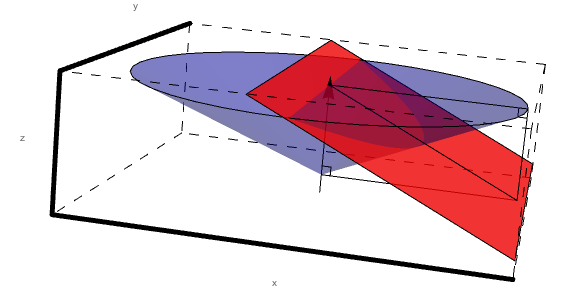
Looking just at sector 1, we can see that the intersection of level 1 and the cone of constant angle theta forms a conic section.

Following the rules of conic sections we know that the eccentricity of the conic is given by:

[math]\e=\frac{\sin [\beta]}{\sin[\alpha]}[/math]

Where β is the angle of the plane, and α is the slant of the cone.

If the conic is an circle, e=0

If the conic is an parabola, e=1

If the conic is an ellipse, [math]e=\sqrt{1-\frac{b^2}{a^2}}[/math]

File:Conic section.png.png