Wire angle correspondance

Determining wire-theta correspondance

To associate the hits with the Moller scattering angle theta, the occupancy plots of the drift chamber hits by means of wire numbers and layer must be translated using the physical constraints of the detector. Using the data released for the DC:

DC: Drift Chambers(specs)

This gives the detector with a working range of 5 to 40 degrees in Theta for the lab frame, with a resolution of 1m radian.

This sets the lower limit:

[math]\frac{5^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.0872664626\ radians[/math]

This sets the upper limit:

[math]\frac{40^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.698131700798\ radians[/math]

Taking the difference,

[math].698131700798-.0872664626\approx\ .61086523198\ radians[/math]

Dividing by 112, we find

[math]\frac{.61086523198}{112}=.005454153912\ radians\approx\ 0.0055\ radians[/math]

CED Verification

Using CED to verify the angle and wire correlation,

Super Layer 1:Layer 1

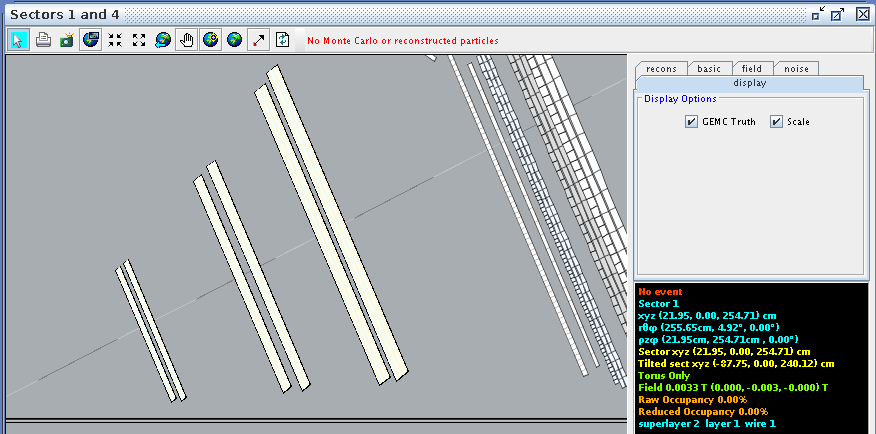
For a hit at layer 1, wire 1 we find the corresponding angle theta in the lab frame to be 4.91 degrees

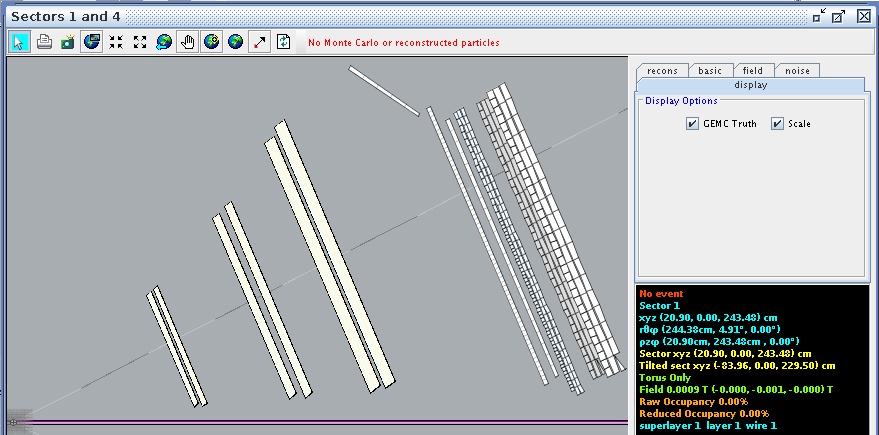
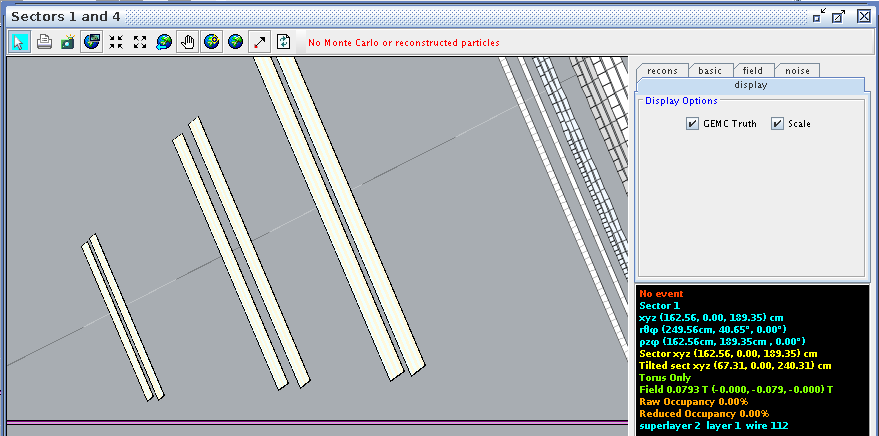
For a hit at layer 1, wire 2 we find the corresponding angle theta in the lab frame to be 5.19 degrees

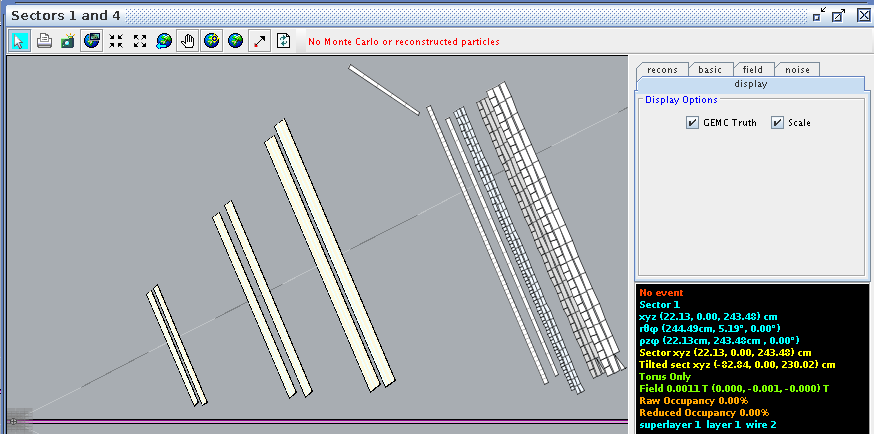
Finding the difference between the two wires,

[math]5.19-4.91=.28^{\circ} \frac{\pi\ radians}{180^{\circ}}=0.004886921906\approx\ 0.00489\ radians[/math]

Examing a hit at layer 1, wire 112 we find the corresponding angle theta in the lab frame to be 40.70 degrees

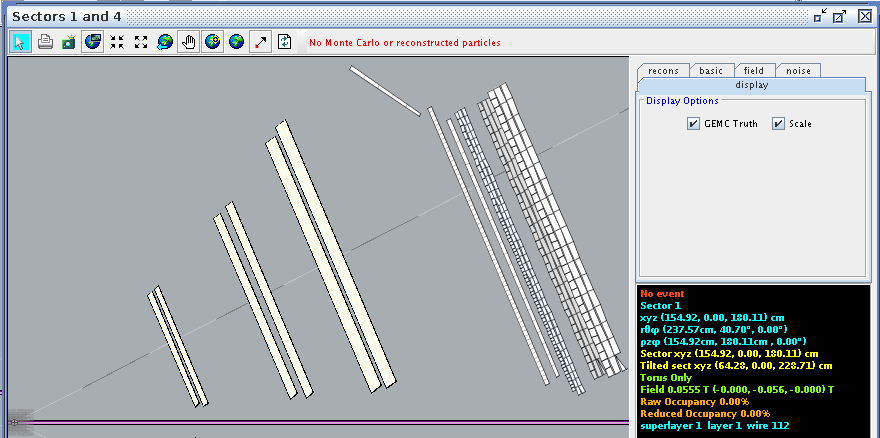
This sets the lower limit:

[math]\frac{4.91^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.085695666273\ radians\approx 0.0857\ radians[/math]

This sets the upper limit:

[math]\frac{40.70^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.710349005562\ radians\approx 0.710\ radians[/math]

Taking the difference,

[math].710349005562-.085695666273\approx\ .625\ radians[/math]

Dividing by 112, we find

[math]\frac{.624653339289}{112}=.005577261958\ radians\approx\ 0.00558\ radians[/math]

Noting the difference from the spacing for a single cell, to the entire detector layer

[math]0.00489-0.00558=0.00069\ \approx .001\ radians[/math]

An uncertainty of this magnitude in radians corresponds to an angular uncertainty of

[math].001\ radian\ \frac{180^{\circ}}{\pi\ radians}\approx .0573^{\circ}[/math]

Testing this for a random angle, 78 degrees we find

[math]0.00558\times 78\ = 0.43524\ radians \frac{180^{\circ}}{\pi\ radians}\approx 24.94^{\circ}[/math]

Adding this to the starting angle of 4.91 degrees

[math]4.91^{\circ}+24.94^{\circ}=29.85^{\circ}\pm .0573^{\circ}[/math]

Comparing this to CED at wire 78

[math]\Longrightarrow 29.85^{\circ}\pm .0573^{\circ}\approx 29.88^{\circ}[/math]

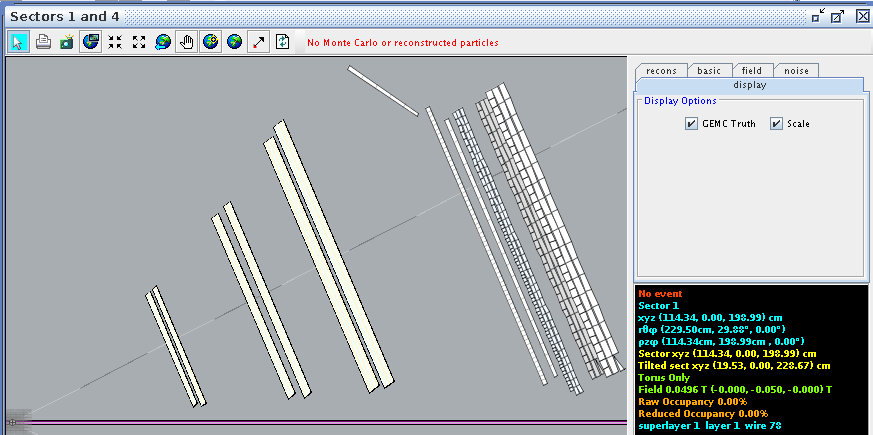
Super Layer 1:Layer 2

For a hit at layer 2, wire 1 we find the corresponding angle theta in the lab frame to be 5.00 degrees

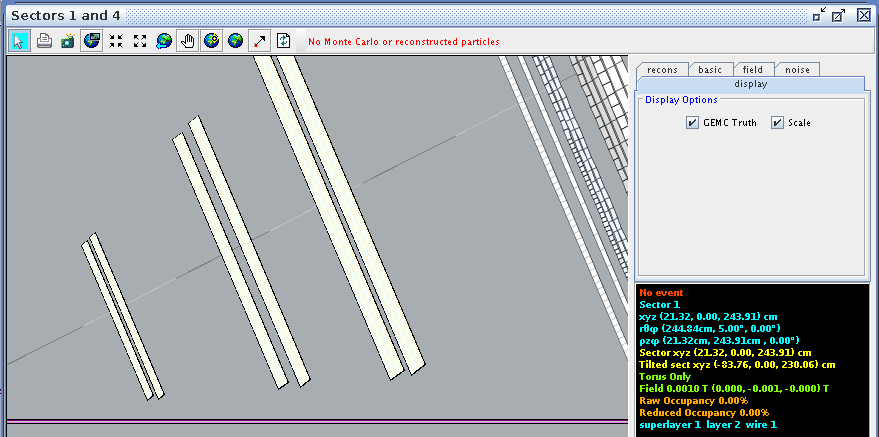
Examing a hit at layer 2, wire 112 we find the corresponding angle theta in the lab frame to be 41.05 degrees

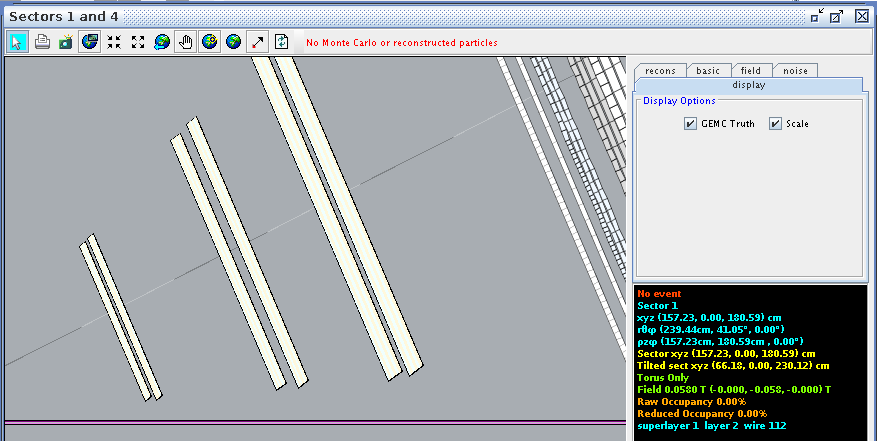
This sets the lower limit:

[math]\frac{5.00^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.0872664626\ radians\approx 0.0873\ radians[/math]

This sets the upper limit:

[math]\frac{40.70^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.716457657944\ radians\approx 0.716\ radians[/math]

Taking the difference,

[math].716457657944-..0872664626\approx\ .629\ radians[/math]

Dividing by 112, we find

[math]\frac{.629191195344}{112}=.00561777853\ radians\approx\ 0.00562\ radians[/math]

Super Layer 1:Layer 6

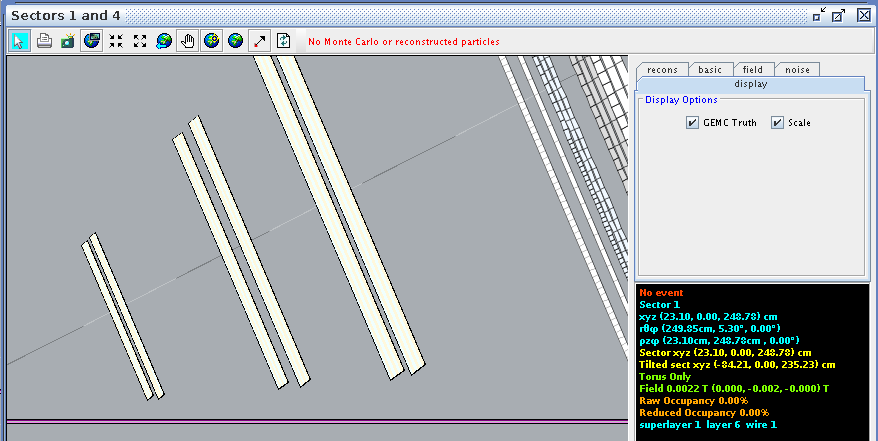
For a hit at layer 2, wire 1 we find the corresponding angle theta in the lab frame to be 5.30 degrees

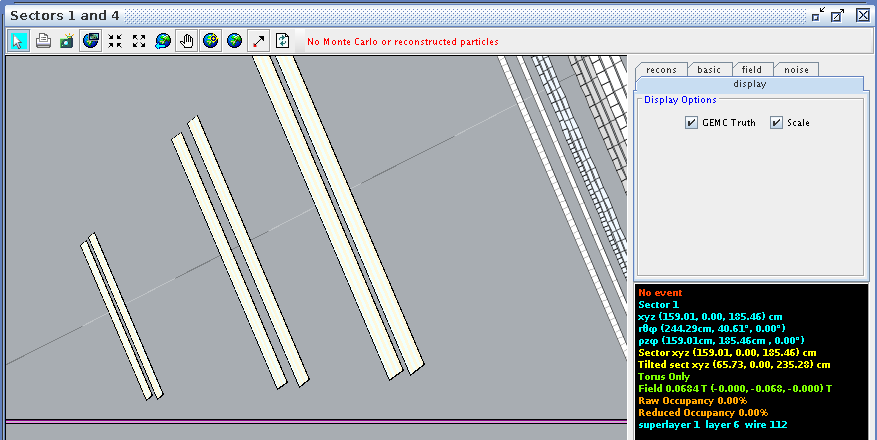
Examing a hit at layer 2, wire 112 we find the corresponding angle theta in the lab frame to be 40.61 degrees

This sets the lower limit:

[math]\frac{5.30^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.09250245\ radians\approx 0.025\ radians[/math]

This sets the upper limit:

[math]\frac{40.61^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.7087782\ radians\approx 0.709\ radians[/math]

Taking the difference,

[math].716457657944-.0872664626\approx\ .616\ radians[/math]

Dividing by 112, we find

[math]\frac{.61627575}{112}=.00550246\ radians\approx\ 0.00550\ radians[/math]

Superlayer 2:Layer 1