Uniform distribution in Energy and Theta LUND files

File:LUND Spread.C

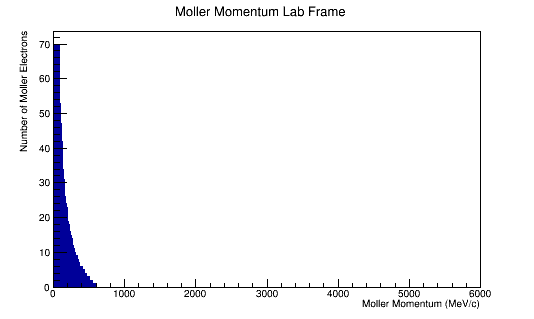
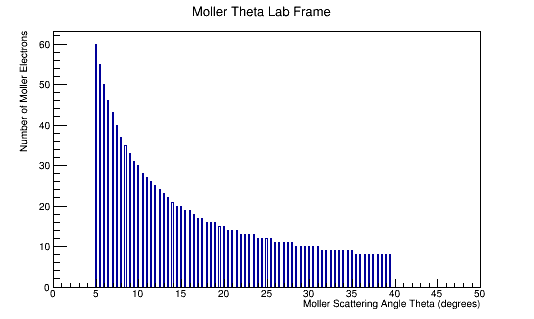
The LUND file is created by creating an isotropic distribution of particles within the energy range of 2MeV-5.5GeV as is found through GEANT simulation. These particles are also uniformly distributed through the angle theta with respect to the beam line in the range 5-40 degrees. This is done at a set angle phi (10 degrees) with respect to the perpendicular components with respect to the beam line.

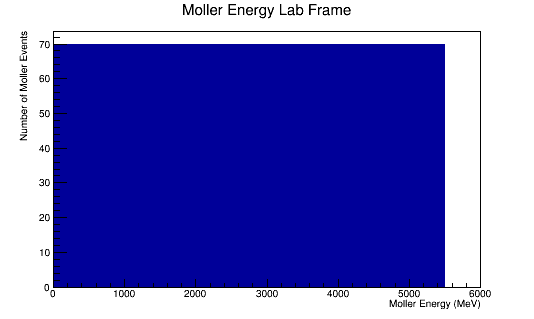
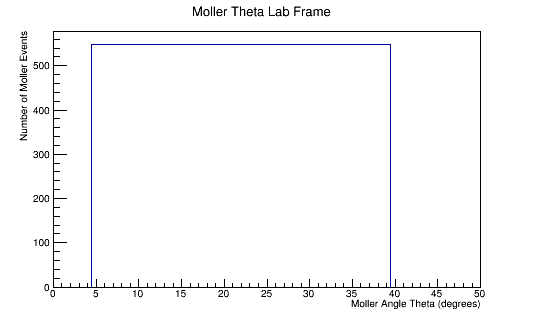
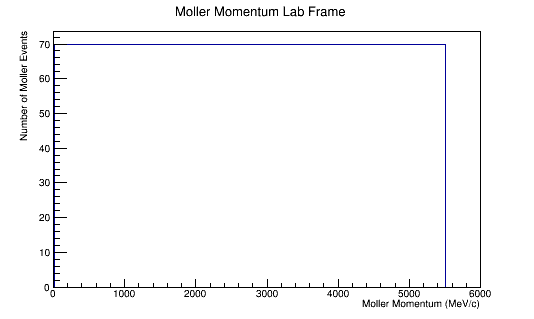
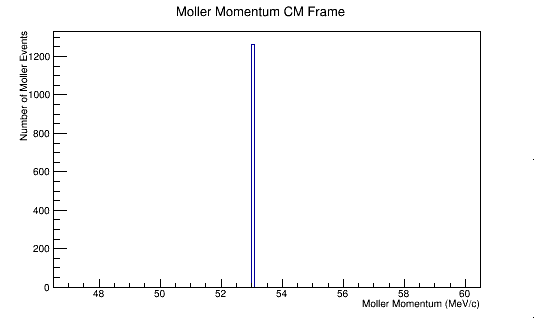
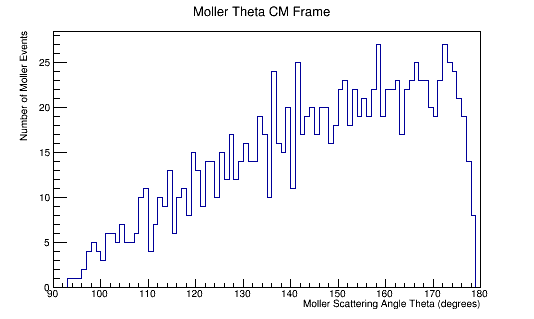
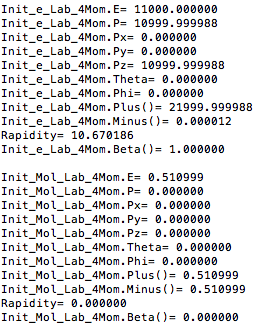
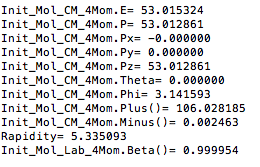
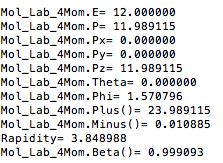
Center of Mass for Stationary Target

For an incoming electron of 11GeV striking a stationary electron we would expect:

Boosting to the Center of Mass Frame:

Phase space Limiting Particles

Since the angle phi has been constrained to remain constant, the x and y components of the momentum will increase in the positive first quadrant. This implies that the z component of the momentum must decrease by the relation:

[math]p^2=p_x^2+p_y^2+p_z^2[/math]

In the Center of Mass frame, this becomes:

[math]p_x^{*2}+p_y^{*2} = p^{*2}-p_z^{*2}[/math]

Since the momentum in the CM frame is a constant, this implies that pz must decrease. For phi=10 degrees:

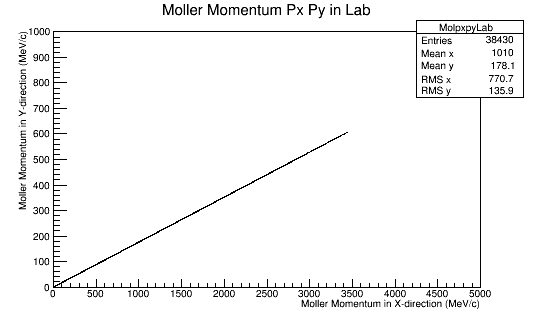
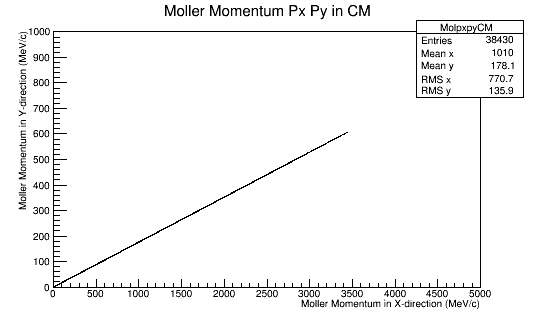
This is repeated for rotations of 60 degrees in phi in the Lab frame.

We can use the variable rapidity:

[math]y \equiv \frac {1}{2} \ln \left(\frac{E+p_z}{E-p_z}\right)[/math]

where

[math] P^+ \equiv E+p_z[/math] [math] P^- \equiv E-p_z[/math]

this implies that as

[math]p_z \rightarrow 0 \Rrightarrow \frac{E+p_z}{E-p_z} \rightarrow 1 \Rrightarrow \ln 1 \rightarrow 0 \Rrightarrow y=0[/math]

For forward travel in the light cone:

[math]p_z \rightarrow E \Rrightarrow \frac{E+p_z}{E-p_z} \rightarrow \infin \Rrightarrow \ln \infin \rightarrow \infin \Rrightarrow y \rightarrow \infin [/math]

For backward travel in the light cone:

[math]p_z \rightarrow -E \Rrightarrow \frac{E+p_z}{E-p_z} \rightarrow 0 \Rrightarrow \ln 0 \rightarrow -\infin \Rrightarrow y \rightarrow -\infin [/math]

For a particle that transforms from the lab frame to a CM frame with the particle inside the light cone:

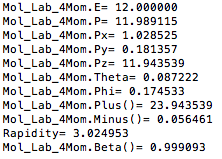
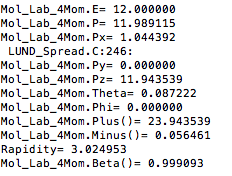
Mol_Lab_4Mom.E= 92.000000
Mol_Lab_4Mom.P= 91.998581
Mol_Lab_4Mom.Px= 51.943569
Mol_Lab_4Mom.Py= 9.159060
Mol_Lab_4Mom.Pz= 75.377159
Mol_Lab_4Mom.Theta= 0.610556
Mol_Lab_4Mom.Phi= 0.174533
Mol_Lab_4Mom.Plus()= 167.377159
Mol_Lab_4Mom.Minus()= 16.622841
Beta= 0.999985
Gamma= 180.041258
Rapidity= 1.154736
 
Mol_CM_4Mom.E= 53.015377
Mol_CM_4Mom.P= 53.012917
Mol_CM_4Mom.Px= 51.943569
Mol_CM_4Mom.Py= 9.159060
Mol_CM_4Mom.Pz= -5.324148
Mol_CM_4Mom.Theta= 1.671397
Mol_CM_4Mom.Phi= 0.174533
Mol_CM_4Mom.Plus()= 47.691229
Mol_CM_4Mom.Minus()= 58.339525
Rapidity= -0.100766

For a particle that transforms from the Lab frame to the CM frame where the particle is not within the light cone:

Mol_Lab_4Mom.E= 92.000000
Mol_Lab_4Mom.P= 91.998581
Mol_Lab_4Mom.Px= 52.589054
Mol_Lab_4Mom.Py= 9.272868
Mol_Lab_4Mom.Pz= 74.914246
Mol_Lab_4Mom.Theta= 0.619278
Mol_Lab_4Mom.Phi= 0.174533
Mol_Lab_4Mom.Plus()= 166.914246
Mol_Lab_4Mom.Minus()= 17.085754
Beta= 0.999985
Gamma= 180.043077
Rapidity= 1.139618
 
Mol_CM_4Mom.E= 53.015377
Mol_CM_4Mom.P= nan
Mol_CM_4Mom.Px= 52.589054
Mol_CM_4Mom.Py= 9.272868
Mol_CM_4Mom.Pz= nan
Mol_CM_4Mom.Theta= nan
Mol_CM_4Mom.Phi= 0.174533
Mol_CM_4Mom.Plus()= nan
Mol_CM_4Mom.Minus()= nan
Rapidity= nan

[math]p_x^2+p_y^2=52.589054^2+9.272868^2=53.400MeV \gt 53.015 MeV (E) \therefore p_z \rightarrow imaginary[/math]

These particles are outside the light cone and are more timelike, thus not visible in normal space. This will reduce the number of particles that will be detected.

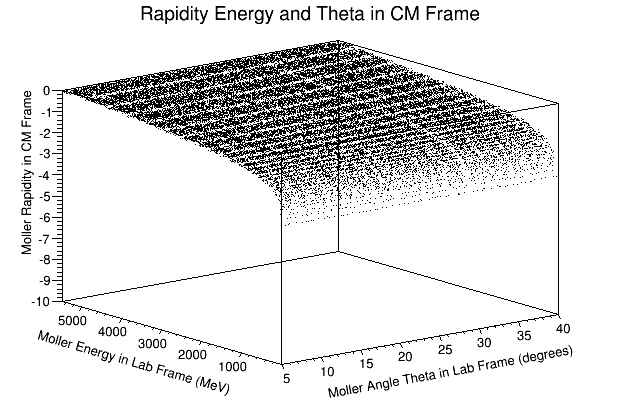
Using Initial Condition based on After Collision in Lab Frame

Starting with the Energy, and a Phi angle of 10 degrees, the 4-momentum vector can be kinematically determined:

Rotating about the z-axis by negative Phi angle, we can eliminate any y-axis component by expressing the vector in x' and z' axis components.

Similarly, by then rotating about the y-axis by negateive Theta, we can express the vector in z' ' components only