Uniform distribution in Energy and Theta LUND files

Creating uniform LUND files

The LUND file is created by creating an isotropic distribution of particles within the energy range of 2MeV-5.5GeV as is found through GEANT simulation. These particles are also uniformly distributed through the angle theta with respect to the beam line in the range 5-40 degrees. This is done at a set angle phi (10 degrees) with respect to the perpendicular components with respect to the beam line.

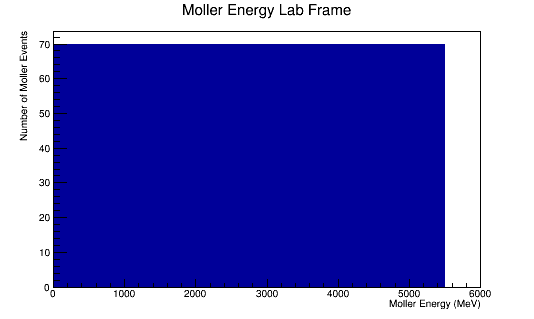
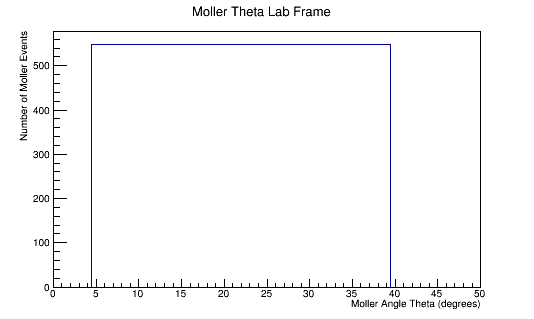
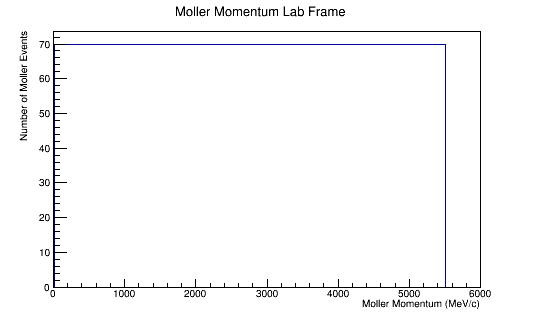
For an incoming electron of 11GeV striking a stationary electron we would expect:

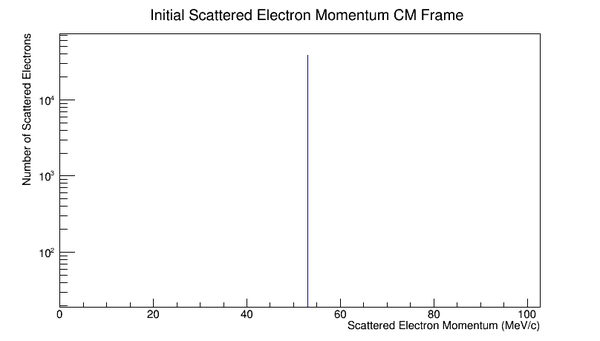
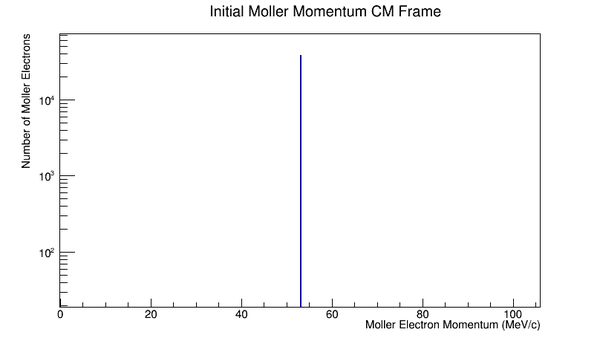
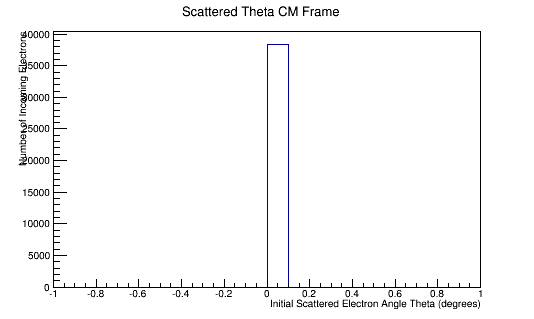
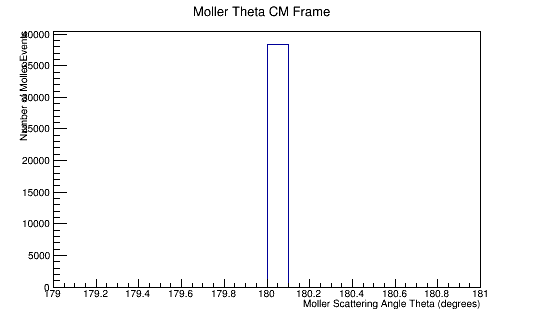
Since the angle phi has been constrained to remain constant, the x and y components of the momentum will increase in the positive first quadrant. This implies that the z component of the momentum must decrease by the relation:

[math]p^2=p_x^2+p_y^2+p_z^2[/math]

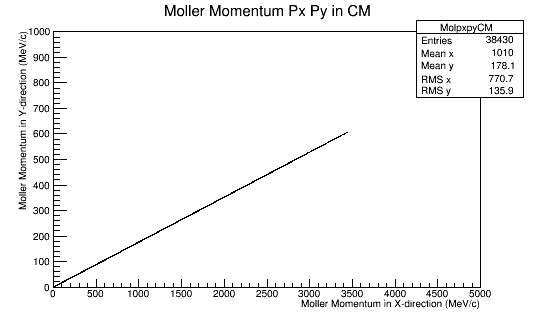
In the Center of Mass frame, this becomes:

[math]p_x^{*2}-p_y^{*2} = p^{*2}-p_z^{*2}[/math]

Since the momentum in the CM frame is a constant, this implies that pz must decrease.

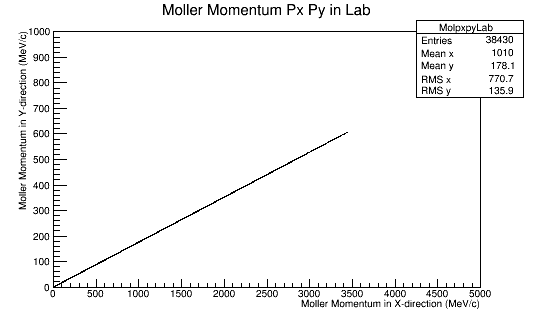
We can use the variable rapidity:

[math]y \equiv \frac {1}{2} \ln \left(\frac{E+p_z}{E-p_z}\right)[/math]

where

[math] P^+ \equiv E+p_z[/math] [math] P^- \equiv E-p_z[/math]

this implies that as

[math]p_z \rightarrow 0 \Rrightarrow \frac{E+p_z}{E-p_z} \rightarrow 1 \Rrightarrow \ln 1 \rightarrow 0 \Rrightarrow y=0[/math]

For forward travel in the light cone:

[math]p_z \rightarrow E \Rrightarrow \frac{E+p_z}{E-p_z} \rightarrow \infin \Rrightarrow \ln \infin \rightarrow \infin \Rrightarrow y \rightarrow \infin [/math]

For backward travel in the light cone:

[math]p_z \rightarrow -E \Rrightarrow \frac{E+p_z}{E-p_z} \rightarrow 0 \Rrightarrow \ln 0 \rightarrow -\infin \Rrightarrow y \rightarrow -\infin [/math]

Mol_Lab_4Mom.E= 92.000000
Mol_Lab_4Mom.P= 91.998581
Mol_Lab_4Mom.Px= 51.943569
Mol_Lab_4Mom.Py= 9.159060
Mol_Lab_4Mom.Pz= 75.377159
Mol_Lab_4Mom.Theta= 0.610556
Mol_Lab_4Mom.Phi= 0.174533
Mol_Lab_4Mom.Plus()= 167.377159
Mol_Lab_4Mom.Minus()= 16.622841
Beta= 0.999985
Gamma= 180.041258
Rapidity= 1.154736
 
Mol_CM_4Mom.E= 53.015377
Mol_CM_4Mom.P= 53.012917
Mol_CM_4Mom.Px= 51.943569
Mol_CM_4Mom.Py= 9.159060
Mol_CM_4Mom.Pz= -5.324148
Mol_CM_4Mom.Theta= 1.671397
Mol_CM_4Mom.Phi= 0.174533
Mol_CM_4Mom.Plus()= 47.691229
Mol_CM_4Mom.Minus()= 58.339525
Rapidity= -0.100766

Mol_Lab_4Mom.E= 92.000000
Mol_Lab_4Mom.P= 91.998581
Mol_Lab_4Mom.Px= 52.589054
Mol_Lab_4Mom.Py= 9.272868
Mol_Lab_4Mom.Pz= 74.914246
Mol_Lab_4Mom.Theta= 0.619278
Mol_Lab_4Mom.Phi= 0.174533
Mol_Lab_4Mom.Plus()= 166.914246
Mol_Lab_4Mom.Minus()= 17.085754
Beta= 0.999985
Gamma= 180.043077
Rapidity= 1.139618
 
Mol_CM_4Mom.E= 53.015377
Mol_CM_4Mom.P= nan
Mol_CM_4Mom.Px= 52.589054
Mol_CM_4Mom.Py= 9.272868
Mol_CM_4Mom.Pz= nan
Mol_CM_4Mom.Theta= nan
Mol_CM_4Mom.Phi= 0.174533
Mol_CM_4Mom.Plus()= nan
Mol_CM_4Mom.Minus()= nan
Rapidity= nan