Difference between revisions of "Looking at effects of Solenoid on Phi Shifts"
| Line 19: | Line 19: | ||
11000 0 0 11000.5 0 0 0 5500.31 28.1338 -44.9298 5500.56 0 0 0 5498.52 -28.1338 44.9298 5498.78 0 0 0</pre> | 11000 0 0 11000.5 0 0 0 5500.31 28.1338 -44.9298 5500.56 0 0 0 5498.52 -28.1338 44.9298 5498.78 0 0 0</pre> | ||
| + | |||
| + | At this energy for the scattered electron: | ||
| + | <pre> | ||
| + | Relativistically, the x and y components remain the same in the conversion from the Lab frame to the Center of Mass frame, since the direction of motion is only in the z direction. | ||
| + | |||
| + | |||
| + | |||
| + | {| class="wikitable" align="center" | ||
| + | | style="background: gray" | <math>p^*_{2(x)}\Leftrightarrow p_{2(x)}'</math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| class="wikitable" align="center" | ||
| + | | style="background: gray" | <math>p^*_{2(y)}\Leftrightarrow p_{2(y)}'</math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | {| class="wikitable" align="center" | ||
| + | | style="background: gray" | <math>p^*_{2(z)}=\sqrt {(p^*_2)^2-(p^*_{2(x)})^2-(p^*_{2(y)})^2}</math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <center>[[File:xz_lab.png | 400 px]]</center> | ||
| + | <center>'''Figure 2: Definition of Moller electron variables in the Lab Frame in the x-z plane.'''</center> | ||
| + | |||
| + | |||
| + | <center><math>\theta '_2\equiv \arccos \left(\frac{p^'_{2(z)}}{p^'_{2}}\right)=\arcos \left(\frac{28.1338}{5500.8154}\equiv 1.5 degrees</math></center></pre> | ||
| + | |||
| + | |||
| + | This is still within the 7 degrees of the detector "cone" with respect to the beam line. | ||
| + | |||
We can alter the lines | We can alter the lines | ||
Revision as of 23:00, 5 April 2016
Using Moller Data to alter energy range
Using the Moller event file MollerScattering_NH3_4e8incident.dat, we can use the fact that GEMC will only create a particle based on the Moller electron. While the data for the scattered electron is passed within a LUND file, kinematically this electron doesn't leave the beam area, and thus never enters the detectors to be recreated. Since the solenoid's purpose is draw electrons trajectories closer the the beam line any electron close the the beam line will be drawn even closer, ensuring that it is never recreated in a GEMC simulation.
We can alter the energy conversion from MollerScattering_NH3_4e8incident.dat to investigate the energy-phi shift relationship
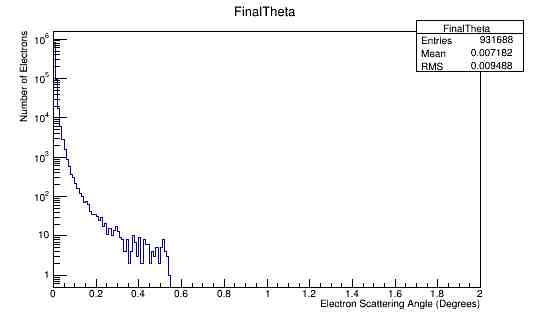
Using the fact that the minimum momentum of MollerScattering_NH3_4e8incident.dat is about 2 MeV,
awk 'NR == 1 {line = $0; min = $15} NR >1 && $15 < min {line =$0; min =$15} END{print line}' MollerScattering_NH3_4e8incident.dat
11000 0 0 11000.5 0 0 0 10997.9 1.42548 -0.177032 10998.4 0 0 0 2.01929 -1.42548 0.177032 2.01939 0 0 0
and the maximum of about 5500 MeV,
awk 'NR == 1 {line = $0; max = $15} NR >1 && $15 > max {line =$0; max =$15} END{print line}' MollerScattering_NH3_4e8incident.dat
11000 0 0 11000.5 0 0 0 5500.31 28.1338 -44.9298 5500.56 0 0 0 5498.52 -28.1338 44.9298 5498.78 0 0 0
At this energy for the scattered electron:
Relativistically, the x and y components remain the same in the conversion from the Lab frame to the Center of Mass frame, since the direction of motion is only in the z direction.
{| class="wikitable" align="center"
| style="background: gray" | <math>p^*_{2(x)}\Leftrightarrow p_{2(x)}'</math>
|}
{| class="wikitable" align="center"
| style="background: gray" | <math>p^*_{2(y)}\Leftrightarrow p_{2(y)}'</math>
|}
{| class="wikitable" align="center"
| style="background: gray" | <math>p^*_{2(z)}=\sqrt {(p^*_2)^2-(p^*_{2(x)})^2-(p^*_{2(y)})^2}</math>
|}
<center>[[File:xz_lab.png | 400 px]]</center>
<center>'''Figure 2: Definition of Moller electron variables in the Lab Frame in the x-z plane.'''</center>
<center><math>\theta '_2\equiv \arccos \left(\frac{p^'_{2(z)}}{p^'_{2}}\right)=\arcos \left(\frac{28.1338}{5500.8154}\equiv 1.5 degrees</math></center>
This is still within the 7 degrees of the detector "cone" with respect to the beam line.
We can alter the lines
Px=evt.FnlMom[0]/1000;
Py=evt.FnlMom[1]/1000;
Pz=evt.FnlMom[2]/1000;
px=evt.MolMom[0]/1000;
py=evt.MolMom[1]/1000;
pz=evt.MolMom[2]/1000;
KE=evt.FnlKE/1000;
ke=evt.MolKE/1000;
Dividing by 1 will give us a distribution of 2GeV-5500 GeV.
Divinding by 10 will give us a distribution of 0.2GeV-550 GeV
Dividing by 100 will give us a distribution of 0.02GeV-55 GeV