Niowave Report 11-30-2015

Overview

This report investigates the impact of target thickness and the use of an external solenoid for the production of positrons using a 10 MeV electron beam. A electron beam energy of 10 MeV is chosen as a compromise between maximizing the production of bremstrahlung photons and minimizing the production of neutrons that occur when an MeV energy electron beam interects with a dense metal. A converter target of liquid Lead-Bismuth Eutectic (LBE) is chosen with a concentration of 44.5% lead and 55.5% bismuth in order to provide a high atomic number (Z) material to increase bremstrahlung production that will also absorb the heat deposited when the material is traversed by an MeV electron beam. This work used the simulation package GEANT4 to predict the impact of target thickness and the use of a solenoid magnetic field on positron production efficiency as well as the amount of energy that will be deposited in the apparatus when using a 3.48 cm diameter beam pipe.

Target optimization

Optimal Thickness

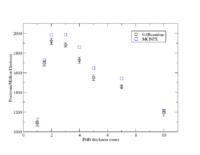
One method to produce positrons relies on the creation of positron-electron pairs from the bremsstrahlung photons that are produced when electrons traverse material with a high atomic number (Z). While thicker material encourages the production of these photons, the increased thickness will also cause the produced positrons to annihilate within the material before they can escape. As a result, there is an optimal thickness which will balance the two processes to maximize positron production. A simulation was performed to determine the optimal thickness using a 10 MeV electron beam with a 1cm radius uniform cylindrical spatial distribution impinging a windowless PbBi target. The target thickness was changed to determine the optimal thickness for emmitt positrons from the downstream surface of the LBE target. The simulation was performed by two separate investigators using separate simulation packages. The results, shown below, indicate that a LBE target thicknes of about 2mm will produce about two positrons for every thousand electrons impinging the LBE target.

Positron production rates as a function of LBE thickness when using a 1 cm radius, 10 MeV electron beam.

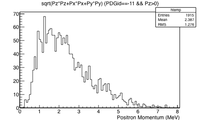
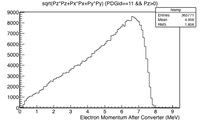
The momentum distribution of positrons escaping the downstream side of the LBE target is shown below along the momentum distribution of electrons that traverse the LBE target. Postrons leaving the downstream side of the target are predicted to have a mean momentum of 2.4 MeV whereas the electrons that penetrate the LBE target will have lost approximately 3 MeV. Most of the positrons have a momentum beetween one and three MeV. A system to transport these electrons would need to cover this momentum range to avoid appreciable loss. A solenoidal magnetic field was chosen that surround the LBD target.

Positron and electron momentum distributions using a 1 cm radius, 10 MeV electron beam impinging a 2mm thick LBE target.

Optimal Solenoidal Field

The use solenoid magnetic field for collecting positrons emmitted on the downstream side of the LBE target was investigated. A solenoidal magnetic field will cause both electrons and positrons to be spiral along the beam pipe in a helical path. The smaller magnetic field is needed to collect the lower momentum positrons relative to the electrons. As the strength of the magnetic field increases, electrons will begin to be spiral down the beam pipe instead of intersecting the beam pipe where they will deposit some energy. The amount of energy deposited by these electrons is the dominant source of beam pipe heating. The magnitude of the magnetic field and the size of the evacuated beam pipe after the target were two parameters that were changed to determine their impact beam pipe heating and the transportation of positrons out of the solenoidal field. A set of 0.25 mm thick stainless steel windows were added to the 2mm thick LBE target for this simulation. A beam pipe thickness of 1.65 mm was assumed.

Beam Pipe heating

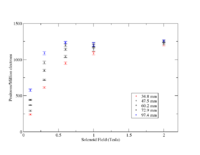
The energy deposited by electrons scattered into a 3.48 diameter stainless steel beam pipe (1.65 mm thick) from a PbBi target as a function of a uniform Solenoidal magnetic field.

The histogram is binned in 100 (10 cm) bin widths. The surface area becomes [math]10 cm \times 2 \pi 3.48/2 = 109.33 cm^2[/math]

To convert From Mev/ e- to kW/cm^2 assuming a current of 1mA (10^-3 C/s) you

[math]\left( \frac{\mbox{MeV}}{\mbox{cm}^2 \mbox{e}^-}\right) \times \left( \frac{ \mbox{e}^-}{1.6 \times 10^{-19}\mbox{C}} \right ) \times \left( \frac{1 \times 10^{-3} \mbox{C}}{\mbox{s}} \right ) \times \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right )[/math]

[math]\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )[/math]

Energy deposited (MeV) along a 1 m long beam pipe of stainless steel 1.65 mm thick.

Positron Rates -vs- Solenoid Field for 2mm thick PbBi target and several Beam pipe diameters

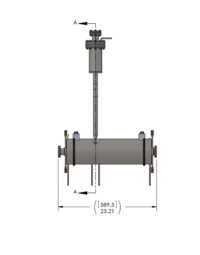
Solenoid Description

A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target. The target is positioned at Z = -901 mm.

Element	dimension
Inner beam pipe radius	1.74 cm
Inner beam pipe thickness	0.165 cm
water jacket thickness	0.457 cm
outer beam pipe radius	2.362 cm
outer beam pipe thickness	0.165 cm
Solenoid inner radius	2.527 cm
Solenoid outer radius	4.406 cm

G4Beamline_PbBi#Reports