Difference between revisions of "DV RunGroupC Moller"
(→Step 1) |
(→Step 1) |
||
| Line 23: | Line 23: | ||
<center>E<sub>cm</sub>=[m<sub>1</sub><sup>2</sup>+m<sub>2</sub><sup>2</sup>+2E<sub>1</sub>E<sub>2</sub>(1-β<sub>1</sub>β<sub>2</sub>cosθ)]<sup>1/2</sup></center> | <center>E<sub>cm</sub>=[m<sub>1</sub><sup>2</sup>+m<sub>2</sub><sup>2</sup>+2E<sub>1</sub>E<sub>2</sub>(1-β<sub>1</sub>β<sub>2</sub>cosθ)]<sup>1/2</sup></center> | ||
| − | In the frame where one particle (m<sub>2</sub>) is at rest | + | where θ is the angle between the particles. In the frame where one particle (m<sub>2</sub>) is at rest |
<center>E<sub>cm</sub>=(m<sub>1</sub><sup>2</sup>+m<sub>2</sub><sup>2</sup>+2E<sub>1 lab</sub>m<sub>2</sub>)<sup>1/2</sup></center> | <center>E<sub>cm</sub>=(m<sub>1</sub><sup>2</sup>+m<sub>2</sub><sup>2</sup>+2E<sub>1 lab</sub>m<sub>2</sub>)<sup>1/2</sup></center> | ||
| + | |||
| + | The velocity of the center of mass in the lab frame is | ||
| + | |||
| + | β<sub>cm</sub>=p<sub>lab</sub>/(E<sub>1 lab</sub>+m<sub>2</sub>), | ||
| + | |||
| + | where p<sub>lab</sub>≡p<sub>1 lab</sub> and | ||
| + | |||
| + | γ<sub>cm</sub>(E<sub>1 lab</sub>+m<sub>2</sub>)/E<sub>cm</sub> | ||
This gives the momenta of the particles in the center of mass to have equal magnitude, but opposite directions | This gives the momenta of the particles in the center of mass to have equal magnitude, but opposite directions | ||
| Line 31: | Line 39: | ||
<center>p<sub>cm</sub>=p<sub>lab</sub>m<sub>2</sub>/E<sub>cm</sub></center> | <center>p<sub>cm</sub>=p<sub>lab</sub>m<sub>2</sub>/E<sub>cm</sub></center> | ||
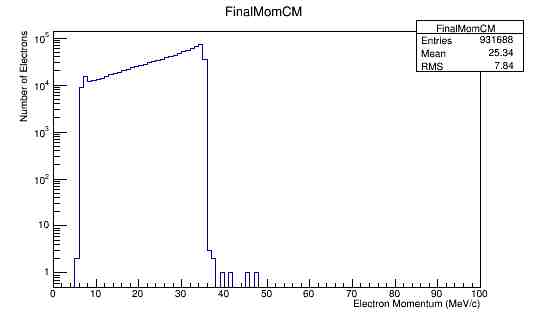
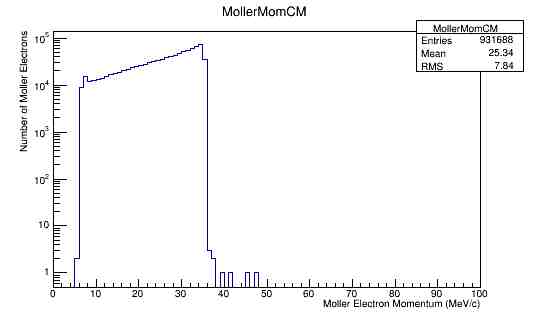
| − | For an incoming electron with momentum of 11GeV, we should find the momentum in the center of mass to be around | + | For an incoming electron with momentum of 11GeV, we should find the momentum in the center of mass to be around 53 GeV which is confirmed in the the plots. |
Revision as of 02:48, 24 April 2015
Simulating the Moller scattering background for EG1
Step 1
Determine the Moller background using an LH2 target to check the physics in GEANT4
Incident electron energy varies from 1-11 GeV.
LH2 target is a cylinder with a 1.5 cm diameter and 1 cm thickness.
(Following dimensions listed on page 8 of File:PHY02-33.pdf)
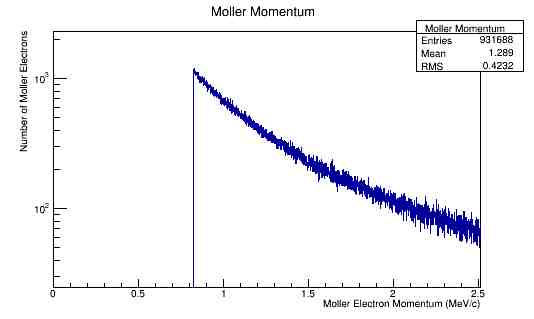
Numbers Moller electrons per incident electron.
While 2nd and 3rd generations are created, only 2 2nd generation daughter particles are created for 1E6 incident particles. All knock on electrons are not counted.
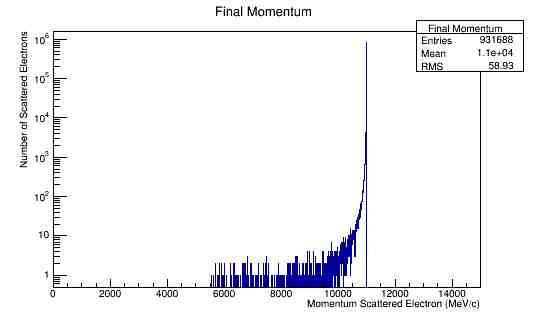
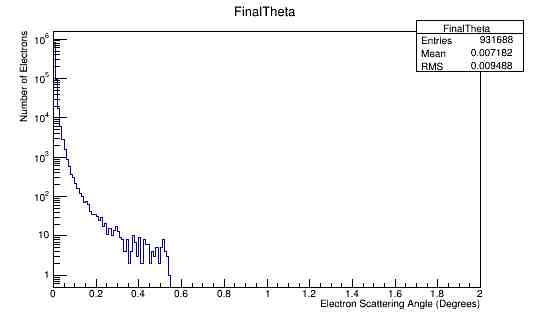
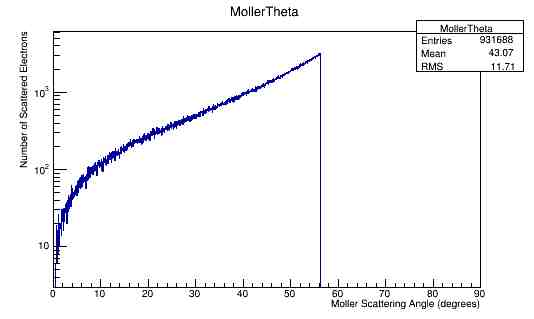
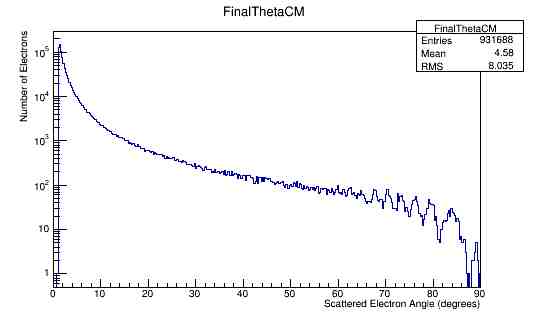
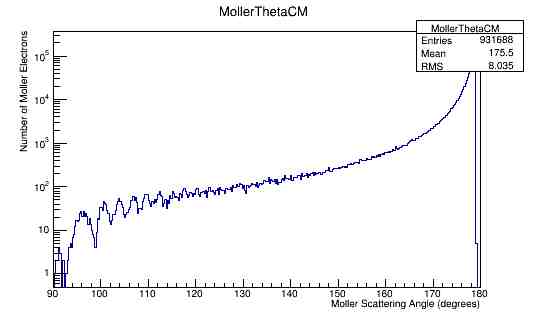
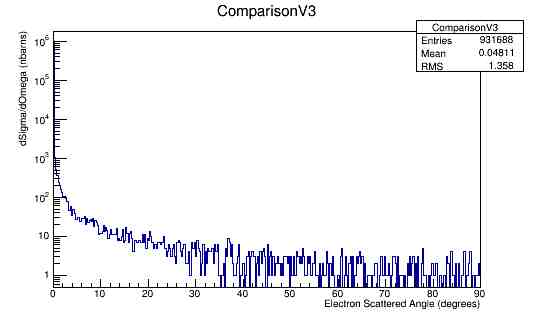
Momentum and angular distributions. 11GeV
In the collision of two particles of mass m1 and m2, the total energy in the center of mass frame can be written
where θ is the angle between the particles. In the frame where one particle (m2) is at rest
The velocity of the center of mass in the lab frame is
βcm=plab/(E1 lab+m2),
where plab≡p1 lab and
γcm(E1 lab+m2)/Ecm
This gives the momenta of the particles in the center of mass to have equal magnitude, but opposite directions
For an incoming electron with momentum of 11GeV, we should find the momentum in the center of mass to be around 53 GeV which is confirmed in the the plots.
Comparing experimental vs. theoretical for Møller differential cross section 11GeV
Step 2
Replace the LH2 target with an NH3 target and compare with LH2 target.
Step 3
Determine impact of Solenoid magnet on Moller events
Papers used
A polarized target for the CLAS detectorFile:PHY02-33.pdf
An investigation of the spin structure of the proton in deep inelastic scattering of polarized muons on polarized protons File:1819.pdf