Difference between revisions of "Forest UCM NLM GalileanTans"
| (24 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | [[File:TF_UCM_GalileanTans_RefFrame.png | 200 px]] | |
| − | + | [[File:TF_UCM_GalileanTans_RefFrame.xfig.txt]] | |
| − | + | Assume that <math>S^{\prime}</math> is a coordinate system moving at a CONSTANT speed <math>v</math> with respect to a fixed coordinate system <math>S</math>. | |
| − | |||
| − | : <math>\ | + | Let <math>\vec{r}</math> and <math>\vec{r}^{\prime}</math> describe the position an object in motion using two different coordinate systems <math>S</math> and <math>S^{\prime}</math> respectively. |
| + | |||
| + | |||
| + | <math>\vec{R}</math> represents a vector that locates the origin of the moving reference frame (<math>S^{\prime}</math>) with respect to the origin of reference from <math>S</math>. | ||
| + | |||
| + | Using the definition of vector addition | ||
| + | |||
| + | :<math>\vec{r} = \vec{R} + \vec{r}^{\prime}</math> | ||
| + | |||
| + | Similarly | ||
| + | |||
| + | :<math>\vec{v} = \frac{d \vec{r}}{dt} = \frac{d \vec{R}}{dt} + \frac{d \vec{r}^{\prime}}{dt} </math> | ||
| + | |||
| + | and | ||
| + | |||
| + | :<math>\vec{a} = \frac{d^2 \vec{r}}{dt^2} = \frac{d^2 \vec{R}}{dt^2} + \frac{d^2 \vec{r}^{\prime}}{dt^2} </math> | ||
| + | |||
| + | |||
| + | Newton's law of motion may be written as | ||
| + | |||
| + | :<math>\vec{F} = m\vec{a} = m \left ( \frac{d^2 \vec{R}}{dt^2} + \frac{d^2 \vec{r}^{\prime}}{dt^2} \right )</math> | ||
| + | |||
| + | |||
| + | If | ||
| + | :<math>\frac{d^2 \vec{R}}{dt^2}=0</math> <math>S^{\prime}</math> is moving at a constant velocity <math>\vec{V}</math> | ||
| + | |||
| + | Then | ||
| + | :<math>\vec{F} = m\vec{a} = m \left ( \frac{d^2 \vec{r}^{\prime}}{dt^2} \right )</math> | ||
| + | |||
| + | Newton's law hold in coordinate system which move at a constant velocity (an inertial reference frame). Accelerating reference frames are know as non-inertial reference frames and will be discussed later. (a coordinate system fixed to the Earth is a non-inertial reference frame since the Earth is rotating about its axis and moving in orbit about the Sun) | ||
| + | |||
| + | =Galiean Transformation to CM frame= | ||
| + | |||
| + | Consider the elastic scattering of two hard spheres from a fixed reference frame (Lab Frame) and an inertial frame moving at a speed <math>\vec{v}_{cm}</math> such that the momentum of the two spheres are equal in magnitude but opposite in direction. | ||
| + | |||
| + | ;A feature of elastic collisions described in the center of momentum (mass) frame is that the magnitude of each particles momentum remains the same before and after a collision, only their directions change. | ||
| + | |||
| + | [[Image:SPIM_ElasCollis_Lab_CM_Frame.jpg | 500 px]] | ||
| + | |||
| + | |||
| + | ; Variable definitions | ||
| + | :<math>m_1</math>= mass of incoming ball | ||
| + | :<math>m_2</math>= mass of target ball | ||
| + | :<math>u_1</math>= iniital velocity of incoming ball in Lab Frame | ||
| + | :<math>v_1</math>= final velocity of <math>m_1</math> in Lab Frame | ||
| + | :<math>\psi</math>= scattering angle of <math>m_1</math> in Lab frame after collision | ||
| + | :<math>u_1^{\prime}</math>= iniital velocity of <math>m_1</math> in C.M. Frame | ||
| + | :<math>v_1^{\prime}</math>= final velocity of <math>m_1</math> in C.M. Frame | ||
| + | :<math>u_2^{\prime}</math>= iniital velocity of <math>m_2</math> in C.M. Frame | ||
| + | :<math>v_2^{\prime}</math>= final velocity of <math>m_2</math> in C.M. Frame | ||
| + | :<math>\theta</math>= scattering angle of <math>m_1</math> in C.M. frame after collision | ||
| + | |||
| + | In terms of our reference frames | ||
| + | |||
| + | ; vector definitions | ||
| + | :<math>\vec{r}_1</math> = a position vector pointing to the location of <math>m_1</math> in the fixed reference frame <math>S</math> | ||
| + | :<math>\vec{r}_2</math> = a position vector pointing to the location of <math>m_2</math> in the fixed reference frame <math>S</math> | ||
| + | :<math>\vec{r}_1^{\prime}</math> = a position vector pointing to the location of <math>m_1</math> in the fixed reference frame <math>S^{\prime}</math> | ||
| + | :<math>\vec{r}_2^{\prime}</math> = a position vector pointing to the location of <math>m_2</math> in the fixed reference frame <math>S^{\prime}</math> | ||
| + | :<math>\vec{R}</math> = a position vector pointing from the fixed reference frame origin to the moving frame origin | ||
| + | |||
| + | ==Find the velocity of the center of momentum (mass) frame== | ||
| + | |||
| + | By definition the velocity of the center of momentum is | ||
| + | |||
| + | :<math>\vec{u}_1 = \vec{v}_{cm} + \vec{u}_1^{\prime}</math> | ||
| + | :<math>\vec{u}_2 = \vec{v}_{cm} + \vec{u}_2^{\prime}</math> | ||
| − | + | In the center of momentum (mass) frame the total momentum is zero | |
| + | ::<math>\vec{p}_1^{\prime} + \vec{p}_2^{\prime} = 0</math> | ||
| + | :: <math>m_1 \vec{u}_1^{\prime} + m_2 \vec{u}_2^{\prime} = 0</math> | ||
| + | :: <math>m_1 \left ( \vec{u}_1 - \vec{v}_{cm} \right ) + m_2 \left ( \vec{u}_2 - \vec{v}_{cm} \right )= 0</math> | ||
| + | :: <math>m_1 \vec{u}_1 + m_2 \vec{u}_2 = \left ( m_1 + m_2 \right ) \vec{v}_{cm} </math> | ||
| − | <math>\ | + | : <math>\vec{v}_{cm} = \frac{m_1 \vec{u}_1 + m_2 \vec{u}_2}{\left ( m_1 + m_2 \right ) }</math> |
| − | + | The above equation is just the calculation of the velocity of the center of mass of the two particle system. | |
| − | + | ;The velocity of the center of momentum frame may be calculated (non-relativistically) as the velocity of the center of mass. | |
| − | |||
| − | |||
| − | + | ==Scattering angles== | |
| − | |||
| − | + | Transforming the scattering angle between reference frames is calculated using the Galilean transformation described by the vector addition of vectors <math>v_1</math> and <math>v_1^\{prime}</math> | |
| − | |||
| − | [[ | + | [[File:SPIM_ElasCollis_Lab_CM_Frame_Velocities.jpg]] |
| − | |||
<math>v_1 \sin(\psi) = v_1^{\prime} \sin(\theta)</math> | <math>v_1 \sin(\psi) = v_1^{\prime} \sin(\theta)</math> | ||
| Line 41: | Line 105: | ||
<math>\tan(\psi) = \frac{\sin(\psi)}{\cos(\psi)} = \frac{v_1^{\prime} \sin(\theta)/v_1}{\frac{v_{CM}}{v_1} + \frac{v_1^{\prime} \cos(\theta)}{v_1} } | <math>\tan(\psi) = \frac{\sin(\psi)}{\cos(\psi)} = \frac{v_1^{\prime} \sin(\theta)/v_1}{\frac{v_{CM}}{v_1} + \frac{v_1^{\prime} \cos(\theta)}{v_1} } | ||
= \frac{\sin(\theta)}{\cos(\theta) + \frac{v_{CM}}{v_1^{\prime}}}</math> | = \frac{\sin(\theta)}{\cos(\theta) + \frac{v_{CM}}{v_1^{\prime}}}</math> | ||
| + | |||
| + | |||
For an elastic collision only the directions change in the CM Frame: <math>u_1^{\prime}= v_1^{\prime}</math> & <math>u_1^{\prime}= v_2^{\prime}</math> | For an elastic collision only the directions change in the CM Frame: <math>u_1^{\prime}= v_1^{\prime}</math> & <math>u_1^{\prime}= v_2^{\prime}</math> | ||
| Line 67: | Line 133: | ||
: <math>\tan(\psi) = \frac{\sin(\theta)}{\cos(\theta) + \frac{m_1}{m_2}}</math> | : <math>\tan(\psi) = \frac{\sin(\theta)}{\cos(\theta) + \frac{m_1}{m_2}}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Now you can transform the angles between the two frames if you know the masses of the two particles. | ||
[[Forest_UCM_NLM#Galilean_Transformations]] | [[Forest_UCM_NLM#Galilean_Transformations]] | ||
Latest revision as of 13:38, 20 August 2014
File:TF UCM GalileanTans RefFrame.xfig.txt
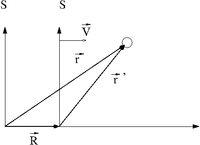
Assume that is a coordinate system moving at a CONSTANT speed with respect to a fixed coordinate system .
Let and describe the position an object in motion using two different coordinate systems and respectively.
represents a vector that locates the origin of the moving reference frame () with respect to the origin of reference from .
Using the definition of vector addition
Similarly
and
Newton's law of motion may be written as
If
- is moving at a constant velocity
Then
Newton's law hold in coordinate system which move at a constant velocity (an inertial reference frame). Accelerating reference frames are know as non-inertial reference frames and will be discussed later. (a coordinate system fixed to the Earth is a non-inertial reference frame since the Earth is rotating about its axis and moving in orbit about the Sun)
Galiean Transformation to CM frame
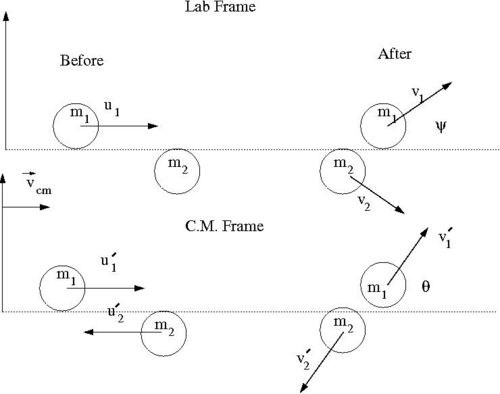
Consider the elastic scattering of two hard spheres from a fixed reference frame (Lab Frame) and an inertial frame moving at a speed such that the momentum of the two spheres are equal in magnitude but opposite in direction.
- A feature of elastic collisions described in the center of momentum (mass) frame is that the magnitude of each particles momentum remains the same before and after a collision, only their directions change.
- Variable definitions
- = mass of incoming ball
- = mass of target ball
- = iniital velocity of incoming ball in Lab Frame
- = final velocity of in Lab Frame
- = scattering angle of in Lab frame after collision
- = iniital velocity of in C.M. Frame
- = final velocity of in C.M. Frame
- = iniital velocity of in C.M. Frame
- = final velocity of in C.M. Frame
- = scattering angle of in C.M. frame after collision
In terms of our reference frames
- vector definitions
- = a position vector pointing to the location of in the fixed reference frame
- = a position vector pointing to the location of in the fixed reference frame
- = a position vector pointing to the location of in the fixed reference frame
- = a position vector pointing to the location of in the fixed reference frame
- = a position vector pointing from the fixed reference frame origin to the moving frame origin
Find the velocity of the center of momentum (mass) frame
By definition the velocity of the center of momentum is
In the center of momentum (mass) frame the total momentum is zero
The above equation is just the calculation of the velocity of the center of mass of the two particle system.
- The velocity of the center of momentum frame may be calculated (non-relativistically) as the velocity of the center of mass.
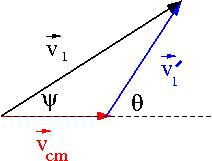
Scattering angles
Transforming the scattering angle between reference frames is calculated using the Galilean transformation described by the vector addition of vectors and
solving for
For an elastic collision only the directions change in the CM Frame: &
- From the definition of the C.M.
- conservation of momentum in CM Frame
- Gallilean Coordinate transformation
- another expression for
using the above gallilean transformation we can do the following
or
Now you can transform the angles between the two frames if you know the masses of the two particles.