|
|
| (18 intermediate revisions by the same user not shown) |
| Line 66: |
Line 66: |
| | :<math>\frac{ d \hat{r}}{dt} = \frac{d \phi}{dt} \hat{\phi}</math> | | :<math>\frac{ d \hat{r}}{dt} = \frac{d \phi}{dt} \hat{\phi}</math> |
| | | | |
| − | Thus for circular motion at a constraint radius we get the familiar expression | + | Thus for circular motion at a constant radius we get the familiar expression |
| | | | |
| | :<math>\vec{v} = \lim_{\Delta t \rightarrow 0} \frac{\vec{r}(t_2)-\vec{r}(t_1)}{\Delta t}= \lim_{\Delta t \rightarrow 0} \frac{r\left( \hat{r}(t_2) - \hat{r}(t_1)\right)}{\Delta t} = r \frac{\Delta \phi}{\Delta t} \hat{\phi} = r \omega \hat{\phi}</math> | | :<math>\vec{v} = \lim_{\Delta t \rightarrow 0} \frac{\vec{r}(t_2)-\vec{r}(t_1)}{\Delta t}= \lim_{\Delta t \rightarrow 0} \frac{r\left( \hat{r}(t_2) - \hat{r}(t_1)\right)}{\Delta t} = r \frac{\Delta \phi}{\Delta t} \hat{\phi} = r \omega \hat{\phi}</math> |
| Line 96: |
Line 96: |
| | :<math>\hat r = \cos \phi \hat{i} + \sin \phi \hat{j}</math> | | :<math>\hat r = \cos \phi \hat{i} + \sin \phi \hat{j}</math> |
| | | | |
| − | :<math>\hat \dot{r} = \frac{d \hat{r}}{d \phi} \frac{d \phi}{d t} =\left( \sin \phi \hat{i} - \cos \phi \hat{j} \right ) \dot{\phi}</math> | + | :<math>\hat \dot{r} = \frac{d \hat{r}}{d \phi} \frac{d \phi}{d t} =\left( -\sin \phi \hat{i} + \cos \phi \hat{j} \right ) \dot{\phi}</math> |
| | :: <math>= \left ( \hat{\phi} \right ) \dot{\phi} </math> | | :: <math>= \left ( \hat{\phi} \right ) \dot{\phi} </math> |
| | | | |
| Line 135: |
Line 135: |
| | Cast the unit vector in terms of cartesian coordinates and take the derivative. | | Cast the unit vector in terms of cartesian coordinates and take the derivative. |
| | | | |
| − | : <math> \hat{\phi} = \sin \phi \hat{i} - \cos \phi \hat{j} </math> | + | : <math> \hat{\phi} = -\sin \phi \hat{i} + \cos \phi \hat{j} </math> |
| | | | |
| | :<math>\hat \dot{\phi} = \frac{d \hat{\phi}}{d \phi} \frac{d \phi}{d t} =\left( -\cos \phi \hat{i} - \sin \phi \hat{j} \right ) \dot{\phi}</math> | | :<math>\hat \dot{\phi} = \frac{d \hat{\phi}}{d \phi} \frac{d \phi}{d t} =\left( -\cos \phi \hat{i} - \sin \phi \hat{j} \right ) \dot{\phi}</math> |
| Line 198: |
Line 198: |
| | another way to determine the unit vector derivative is to cast them in terms of cartesian coordinate. | | another way to determine the unit vector derivative is to cast them in terms of cartesian coordinate. |
| | | | |
| − | :<math>\hat{r} = \frac{\vec{r}}{|\vec{r}|} =\cos \phi \sin \theta \hat{i} + \sin \phi \sin \theta \hat{j} + \cos \theta \hat{k}</math> | + | :<math>\hat{r} = \frac{\vec{r}}{|\vec{r}|} =\cos \phi \sin \theta \hat{i} + \sin \phi \sin \theta \hat{j} + \cos \theta \hat{k}= \frac{\frac{\partial \vec{r}}{\partial r}}{\left | \frac{\partial \vec{r}}{\partial r}\right | } </math> |
| | | | |
| − | :<math>\hat{\phi} = \frac{\hat {z} \times \hat {r} }{\sin \theta}=- \sin \phi \hat{i} + \cos \phi \hat{k}</math> | + | :<math>\hat{\phi} = \frac{\frac{\partial \vec{r}}{\partial \phi}}{\left | \frac{\partial \vec{r}}{\partial \phi}\right | } =- \sin \phi \hat{i} + \cos \phi \hat{j}= \frac{\hat {z} \times \hat {r} }{\sin \theta}</math> |
| | | | |
| − | :<math>\hat{\theta} = \hat{\phi} \times \hat {r} =-\cos \phi \cos \theta \hat{i} - \sin \phi \cos \theta \hat{j} + \sin \theta \hat{k}</math> | + | :<math>\hat{\theta} = -\hat{\phi} \times \hat {r} =\cos \phi \cos \theta \hat{i} + \sin \phi \cos \theta \hat{j} - \sin \theta \hat{k}</math> |
| | | | |
| | The derivative of the above unit vectors are | | The derivative of the above unit vectors are |
| Line 219: |
Line 219: |
| | | | |
| | | | |
| − | :<math>\vec{a}</math> = <math>\frac{d \vec{v}}{dt}</math> = <math>\frac{d^2 x}{dt^2}\hat{i} + \frac{d^2 y}{dt^2}\hat{j} + \frac{d^2 z}{dt^2}\hat{k} </math> | + | :<math>\vec{a}</math>= <math>\frac{d}{dt} \left ( \dot{r} \hat{r} + r \left ( \dot{\theta} \hat{\theta} + \dot{\phi} \sin \theta \hat {\phi} \right ) \right )</math> |
| − | ::<math>\ddot{r} -r \dot{\theta}^2 \cos^2{\phi} -r \dot{\phi}^2) \frac{d^2 x}{dt^2}\hat{i} + \frac{d^2 y}{dt^2}\hat{j} + \frac{d^2 z}{dt^2}\hat{k} </math>
| |
| | | | |
| | + | ::=<math> \ddot{r} \hat{r} + \dot{r} \dot{\hat{r}} </math> |
| | + | :: <math>+ \dot{r} \dot{\theta} \hat{\theta} + r \ddot{\theta} \hat{\theta} + r \dot{\theta} \dot{\hat{\theta}}</math> |
| | + | :: <math>+ \dot{r} \dot{\phi} \sin \theta \hat {\phi} + r \ddot{\phi} \sin \theta \hat {\phi} + r \dot{\phi} \dot{\sin \theta} \hat {\phi} + r \dot{\phi} \sin \theta \dot{\hat {\phi}}</math> |
| | + | :: = <math>\left ( \ddot{r} - r \dot{\theta}^2 - r \dot{\phi}^2 \sin \theta \right) \hat{r} |
| | + | + \left( r \ddot{\theta} + 2 r \dot{\theta} - r \dot{\phi}^2 \sin \theta \cos \theta \right) \hat{\theta} |
| | + | + \left ( r \ddot{\phi} \sin \theta + 2 r \dot{\theta} \dot{\phi} \cos \theta + 2 \dot{r} \dot{\phi} \sin \theta \right ) \hat{\phi} |
| | + | </math> |
| | | | |
| | | | |
| | [[Forest_UCM_NLM#Space]] | | [[Forest_UCM_NLM#Space]] |
Latest revision as of 20:23, 27 August 2021
Cartesian, Spherical, and Cylindrical coordinate systems are commonly used to describe three-dimensional space.
Cartesian
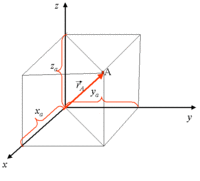
Vector Notation convention:
Position:
- [math]\vec{r} = x \hat{i} + y \hat{j} + z \hat{k} = (x,y,z) = \sum_1^3 r_i \hat{e}_i[/math]
Velocity and Acceleration vector in cartesian coordinates
- [math]\vec{v}[/math] = [math]\frac{d \vec{r}}{dt}[/math] = [math]\frac{d x}{dt}\hat{i} + x\frac{d \hat{i}}{dt} + \cdots[/math]
cartesian unit vectors do not change with time (unit vectors for other coordinate system types do)
- [math]\frac{d \hat{i}}{dt} =0 =\frac{d \hat{j}}{dt} =\frac{d \hat{k}}{dt}[/math]
- [math]\vec{v}[/math] = [math]\frac{d \vec{r}}{dt}[/math] = [math]\frac{d x}{dt}\hat{i} + \frac{d y}{dt}\hat{j} + \frac{d z}{dt}\hat{k} [/math]
Similarly Acceleration is given by
- [math]\vec{a}[/math] = [math]\frac{d \vec{v}}{dt}[/math] = [math]\frac{d^2 x}{dt^2}\hat{i} + \frac{d^2 y}{dt^2}\hat{j} + \frac{d^2 z}{dt^2}\hat{k} [/math]
Polar
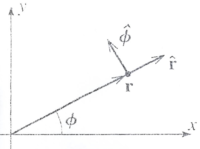 Vector Notation convention:
Vector Notation convention:
Position:
Because [math]\hat{r}[/math] points in a unique direction given by [math]\hat{r} = \frac{\vec{r}}{|r|}[/math] we can write the position vector as
- [math]\vec{r} = r \hat{r}[/math]
- [math]\vec{r} \ne r \hat{r} +\phi \hat{\phi} [/math]: [math]\phi[/math] does not have the units of length
The unit vectors ([math]\hat{r}[/math] and [math]\hat{\phi}[/math] ) are changing in time. You could express the position vector in terms of the cartesian unit vectors in order to avoid this
- [math]\vec{r} = r \cos(\phi) \hat{i} + r \sin(\phi)\hat{j}[/math]
The dependence of position with [math]\phi[/math] can be seen if you look at how the position changes with time.
Velocity in Polar Coordinates
Consider the motion of a particle in a circle. At time [math]t_1[/math] the particle is at [math]\vec{r}(t_1)[/math] and at time [math]t_2[/math] the particle is at [math]\vec{r}(t_2)[/math]
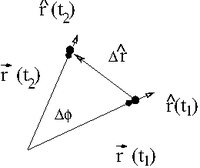
If we take the limit [math]t_2 \rightarrow t_1[/math] ( or [math]\Delta t \rightarrow 0[/math]) then we can write the velocity of this particle traveling in a circle as
- [math]\hat{r} (t_2)-\hat{r}(t_1) \equiv \Delta \hat{r} = \Delta \phi \hat{\phi}[/math]
- or
- [math]\frac{ d \hat{r}}{dt} = \frac{d \phi}{dt} \hat{\phi}[/math]
Thus for circular motion at a constant radius we get the familiar expression
- [math]\vec{v} = \lim_{\Delta t \rightarrow 0} \frac{\vec{r}(t_2)-\vec{r}(t_1)}{\Delta t}= \lim_{\Delta t \rightarrow 0} \frac{r\left( \hat{r}(t_2) - \hat{r}(t_1)\right)}{\Delta t} = r \frac{\Delta \phi}{\Delta t} \hat{\phi} = r \omega \hat{\phi}[/math]
- [math]\vec{v} = r \frac{d \phi}{dt} \hat{\phi}[/math]
If the particle is not constrained to circular motion ( i.e.: [math]r[/math] can change with time) then the velocity vector in polar coordinates is
- [math]\vec{v}[/math] = [math]\frac{d r}{dt}\hat{r} + r\frac{d \phi}{dt} \hat{\phi}[/math]
- or in more compact form
- [math]\vec{v}=\vec{\dot{r}} = \dot{r} \hat{r} + r \dot{\phi} \hat{\phi}= v_r \hat{r} + v_{\phi} \hat{\phi}[/math]
- linear velocity [math]\equiv v_r [/math] Angular velocity [math]\equiv v_{\phi} [/math]
- Finding the derivative directly
Cast the unit vector in terms of cartesian coordinates and take the derivative.
- [math]\hat r = \cos \phi \hat{i} + \sin \phi \hat{j}[/math]
- [math]\hat \dot{r} = \frac{d \hat{r}}{d \phi} \frac{d \phi}{d t} =\left( -\sin \phi \hat{i} + \cos \phi \hat{j} \right ) \dot{\phi}[/math]
- [math]= \left ( \hat{\phi} \right ) \dot{\phi} [/math]
Acceleration in Polar Coordinates
Taking the derivative of velocity with time gives the acceleration
- [math]\vec{a} = \frac{d \vec{v}}{dt} =\vec{\ddot{r}} [/math]
- [math]= \frac{ d \left (\dot{r} \hat{r} + r \dot{\phi} \hat{\phi}= v_r \hat{r} + v_{\phi} \hat{\phi}\right)}{dt}[/math]
- [math]= \left ( \frac{ d \dot{r}}{dt} \hat{r} + \dot{r} \frac{ d\hat{r}}{dt} \right) + \left ( \frac{d r}{dt} \dot{\phi} \hat{\phi} +r \frac{d \dot{\phi}}{dt} \hat{\phi} +r \dot{\phi} \frac{d \hat{\phi}}{dt} \right )[/math]
- [math]= \left ( \ddot{r} \hat{r} + \dot{r} \dot{\phi}\hat{\phi} \right) + \left ( \dot{r} \dot{\phi} \hat{\phi} +r \ddot{\phi} \hat{\phi} +r \dot{\phi} \frac{d \hat{\phi}}{dt} \right )[/math]
We need to find the derivative of the unit vector [math]\hat{\phi}[/math] with time.
Consider the position change below in terms of only the unit vector [math]\hat{\phi}[/math]
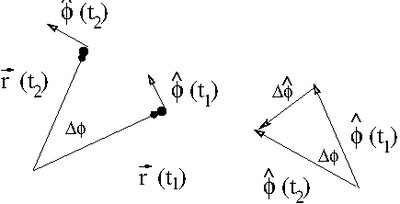
Using the same arguments used to calculate the rate of change in [math]\hat{r}[/math]:
If we take the limit [math]t_2 \rightarrow t_1[/math] ( or [math]\Delta t \rightarrow 0[/math]) then we can write the velocity of this particle traveling in a circle as
- [math]\hat{\phi} (t_2)-\hat{\phi}(t_1) \equiv \Delta \hat{\phi} = \Delta \phi (- \hat{r})[/math]
- or
- [math]\frac{ d \hat{\phi}}{dt} = -\frac{d \phi}{dt} \hat{r}[/math]
- [math]\frac{d \hat{\phi}}{dt}= -\dot{\phi} \hat{r}[/math]
- Finding the derivative of [math]\hat{\phi}[/math] directly
Cast the unit vector in terms of cartesian coordinates and take the derivative.
- [math] \hat{\phi} = -\sin \phi \hat{i} + \cos \phi \hat{j} [/math]
- [math]\hat \dot{\phi} = \frac{d \hat{\phi}}{d \phi} \frac{d \phi}{d t} =\left( -\cos \phi \hat{i} - \sin \phi \hat{j} \right ) \dot{\phi}[/math]
- [math]= \left (- \hat{r} \right ) \dot{\phi} [/math]
Substuting the above into our calculation for acceleration:
- [math]\vec{a} = \left ( \ddot{r} \hat{r} + \dot{r} \dot{\phi}\hat{\phi} \right) + \left ( \dot{r} \dot{\phi} \hat{\phi} +r \ddot{\phi} \hat{\phi} +r \dot{\phi} \frac{d \hat{\phi}}{dt} \right )[/math]
- [math]= \left ( \ddot{r} \hat{r} + \dot{r} \dot{\phi}\hat{\phi} \right) + \left ( \dot{r} \dot{\phi} \hat{\phi} +r \ddot{\phi} \hat{\phi} +r \dot{\phi} \left( -\dot{\phi} \hat{r}\right) \right )[/math]
- [math]= \left ( \ddot{r} -r\dot{\phi}^2 \right) \hat{r} + \left ( 2\dot{r} \dot{\phi} +r \ddot{\phi} \right ) \hat{\phi} [/math]
For the case of circular motion at constant [math] r (\dot{r} = 0)[/math]
- [math]\vec{a} = -r\dot{\phi}^2 \hat{r} + r \ddot{\phi} \hat{\phi} [/math]
radial (centripetal, center seeking) acceleration [math]\equiv -r\dot{\phi}^2 \hat{r} = -r \omega^2 \hat{r}[/math]
angular (tangential) acceleration [math]\equiv r \ddot{\phi} \hat{\phi} = r \alpha \hat{\phi}[/math]
If [math]\dot{r} \ne 0[/math]
Then there are two additional terms
- [math]\ddot{r} \hat {r}[/math] = radial acceleration
- [math]2\dot{r} \dot{\phi} \hat {\phi}[/math] = Coriolis acceleration (to be described later)
Cylindrical
Cylindrical coordinates are polar coordinates with a third dimension usually labeled [math](z)[/math]
change picture so angle is [math]\phi[/math] not [math]\theta[/math]
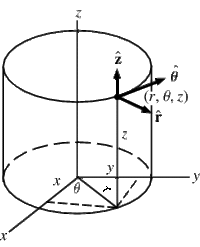
We just need to add [math]z\hat{k}[/math] to all the vectors (remember [math]\hat{\dot{k}} = 0[/math])
- [math]\vec{r} = r \hat{r} + z \hat{k}[/math]
- [math]\vec{v}=\vec{\dot{r}} = \dot{r} \hat{r} + r \dot{\phi} \hat{\phi} + \dot{z} \hat{k}[/math]
- [math]\vec{a} = \left ( \ddot{r} -r\dot{\phi}^2 \right) \hat{r} + \left ( 2\dot{r} \dot{\phi} +r \ddot{\phi} \right ) \hat{\phi} + \ddot{z} \hat{k}[/math]
Spherical
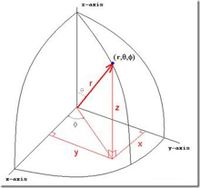
Position:
- [math]\vec{r} = r \hat{r} [/math]
Velocity vector in Spherical coordinates
- [math]\vec{v}[/math] = [math]\frac{d \vec{r}}{dt}[/math] = [math]\frac{d r}{dt}\hat{r} + r\frac{d \hat{r}}{dt} [/math]
another way to determine the unit vector derivative is to cast them in terms of cartesian coordinate.
- [math]\hat{r} = \frac{\vec{r}}{|\vec{r}|} =\cos \phi \sin \theta \hat{i} + \sin \phi \sin \theta \hat{j} + \cos \theta \hat{k}= \frac{\frac{\partial \vec{r}}{\partial r}}{\left | \frac{\partial \vec{r}}{\partial r}\right | } [/math]
- [math]\hat{\phi} = \frac{\frac{\partial \vec{r}}{\partial \phi}}{\left | \frac{\partial \vec{r}}{\partial \phi}\right | } =- \sin \phi \hat{i} + \cos \phi \hat{j}= \frac{\hat {z} \times \hat {r} }{\sin \theta}[/math]
- [math]\hat{\theta} = -\hat{\phi} \times \hat {r} =\cos \phi \cos \theta \hat{i} + \sin \phi \cos \theta \hat{j} - \sin \theta \hat{k}[/math]
The derivative of the above unit vectors are
- [math]\dot{\hat{r}} = \dot{\theta} \hat{\theta} + \dot{\phi} \sin \theta \hat {\phi}[/math]
- [math]\dot{\hat{\phi}} = -\dot{\phi} \left ( \sin \theta \hat{r} + \cos \theta \hat {\theta} \right )[/math]
- [math]\dot{\hat{\theta}} = -\dot{\theta} \hat{r} + \dot{\phi} \cos \theta \hat {\phi}[/math]
substituting the above into the definition of velocity
- [math]\vec{v}[/math] = [math]\frac{d r}{dt}\hat{r} + r\frac{d \hat{r}}{dt} [/math]
- = [math]\dot{r} \hat{r} + r \left ( \dot{\theta} \hat{\theta} + \dot{\phi} \sin \theta \hat {\phi} \right )[/math]
Acceleration vector in Spherical coordinates
- [math]\vec{a}[/math]= [math]\frac{d}{dt} \left ( \dot{r} \hat{r} + r \left ( \dot{\theta} \hat{\theta} + \dot{\phi} \sin \theta \hat {\phi} \right ) \right )[/math]
- =[math] \ddot{r} \hat{r} + \dot{r} \dot{\hat{r}} [/math]
- [math]+ \dot{r} \dot{\theta} \hat{\theta} + r \ddot{\theta} \hat{\theta} + r \dot{\theta} \dot{\hat{\theta}}[/math]
- [math]+ \dot{r} \dot{\phi} \sin \theta \hat {\phi} + r \ddot{\phi} \sin \theta \hat {\phi} + r \dot{\phi} \dot{\sin \theta} \hat {\phi} + r \dot{\phi} \sin \theta \dot{\hat {\phi}}[/math]
- = [math]\left ( \ddot{r} - r \dot{\theta}^2 - r \dot{\phi}^2 \sin \theta \right) \hat{r}
+ \left( r \ddot{\theta} + 2 r \dot{\theta} - r \dot{\phi}^2 \sin \theta \cos \theta \right) \hat{\theta}
+ \left ( r \ddot{\phi} \sin \theta + 2 r \dot{\theta} \dot{\phi} \cos \theta + 2 \dot{r} \dot{\phi} \sin \theta \right ) \hat{\phi}
[/math]
Forest_UCM_NLM#Space





