Difference between revisions of "05/11/2011"

From New IAC Wiki
Jump to navigation Jump to search
 
(10 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
Below my calibration line for n's detector with HAMAMATSU PMT (-1500 V):
+
[https://wiki.iac.isu.edu/index.php/N%27s_detector_calibration Go Back]
 +
 
 +
 
 +
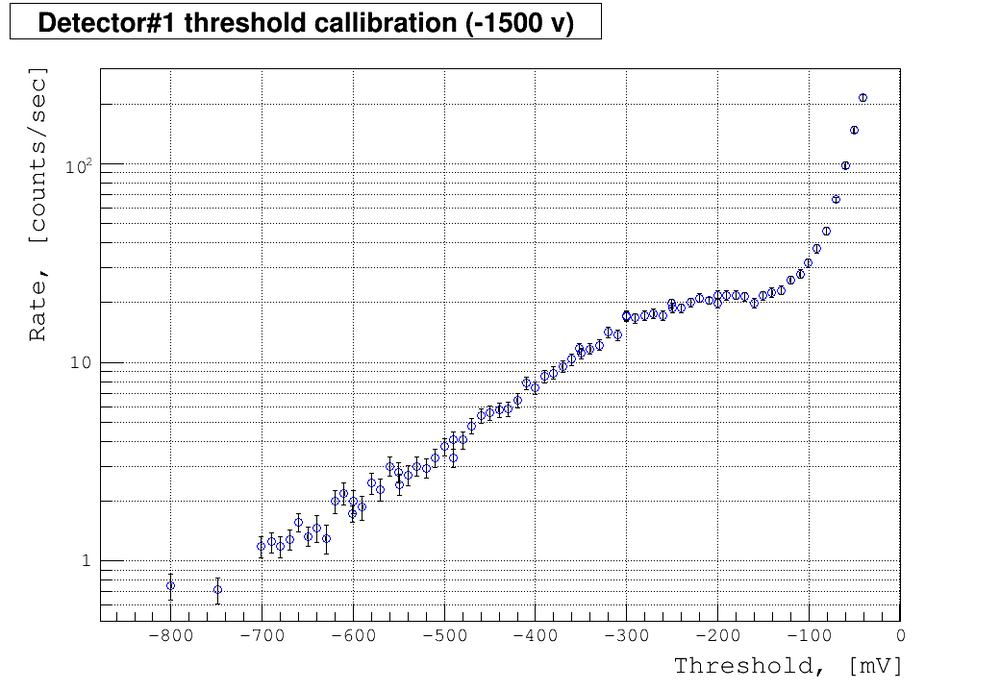
Because is something wrong I decided to measure the counts rate as function of threshold energy. Maybe my threshold was incorrect.
 +
 
 +
Below are my results for n's detector with HAMAMATSU PMT (-1500 V):
  
 
[[File:Det1 callibration.png | 1000 px]]
 
[[File:Det1 callibration.png | 1000 px]]
 +
 +
 +
 +
So it looks like my previous threshold value (-500 mV) was not good. Let's set it up the -200 mV. And let's see does the n's detector sensitive to the source. The same set up and distances as before.
 +
{| border="1" cellspacing="0" style="text-align: center; width: 800px; height: 100px;"
 +
! scope="col" width="50" |
 +
! scope="col" width="50" | counts/sec (5 min test), no source
 +
! scope="col" width="50" | counts/sec (5 min test), with source on the top of PS1
 +
|-
 +
!n's
 +
|19.89<math>\pm</math>0.26  (total 5966 cnts) || 58.84<math>\pm</math>0.29  (total 17652 cnts)
 +
|}
 +
 +
So now we see the source. The ratio are:
 +
 +
<math>\frac{Rate_{source}}{Rate_{w/source}} = \frac{58.84}{19.89} = 2.96 </math>

Latest revision as of 04:59, 12 May 2011

Go Back


Because is something wrong I decided to measure the counts rate as function of threshold energy. Maybe my threshold was incorrect.

Below are my results for n's detector with HAMAMATSU PMT (-1500 V):

Det1 callibration.png


So it looks like my previous threshold value (-500 mV) was not good. Let's set it up the -200 mV. And let's see does the n's detector sensitive to the source. The same set up and distances as before.

counts/sec (5 min test), no source counts/sec (5 min test), with source on the top of PS1
n's 19.89[math]\pm[/math]0.26 (total 5966 cnts) 58.84[math]\pm[/math]0.29 (total 17652 cnts)

So now we see the source. The ratio are: 

[math]\frac{Rate_{source}}{Rate_{w/source}} = \frac{58.84}{19.89} = 2.96 [/math]
Retrieved from "https://wiki.iac.isu.edu/index.php?title=05/11/2011&oldid=62749"