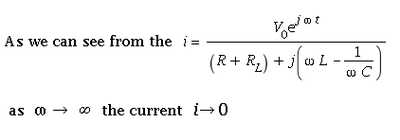Difference between revisions of "Lab 5 RS"
Jump to navigation
Jump to search
(Created page with 'LC Resonance circuits =The LC cicuit= 200 px #Design a '''parallel''' LC resonant circuit with a resonant frequency between 50-200 kHz. use <math>L<…') |
|||
| (66 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | LC Resonance circuits | + | [https://wiki.iac.isu.edu/index.php/Electronics_RS Go Back to All Lab Reports] |
| − | =The LC | + | |
| + | |||
| + | ;LC Resonance circuits | ||
| + | =The LC circuit= | ||
| + | |||
[[File:TF_EIM_Lab5_LC.png| 200 px]] | [[File:TF_EIM_Lab5_LC.png| 200 px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Design a '''parallel''' LC resonant circuit with a resonant frequency between 50-200 kHz. use <math>L</math> = 10 - 100 <math>\mu H</math>, R = 1k <math>\Omega</math>== |
| + | |||
| + | :<math>\omega_0=\frac{1}{\sqrt{\mbox{LC}}}</math> | ||
| + | |||
| + | I choose the following values for <math>\mbox{L}</math> and <math>\mbox{C}</math>: | ||
| + | |||
| + | :<math>\mbox{L}=33\ \mu H</math> | ||
| + | :<math>\mbox{C}=1.024\ \mu F</math> | ||
| + | :<math>\mbox{R}=0.989\ k \Omega</math> | ||
| + | :<math>\mbox{R}_L=2.5\ \Omega</math> | ||
| + | |||
| + | So the resonance frequency is <math>\omega_0=\frac{1}{\sqrt{33\ \mu H \cdot 1.024\ \mu F}} = 172 \cdot 10^3\ \frac{\mbox{rad}}{\mbox{sec}}</math> | ||
| + | |||
| + | :<math>f=\frac{\omega_0}{2\pi} = 27.4\ \mbox{kHz}</math> | ||
| + | |||
| + | And | ||
| + | |||
| + | :<math>\mbox{Q} = \frac{1}{\mbox{R}} \sqrt{\frac{\mbox{L}}{\mbox{C}}} = 2.27</math> | ||
| + | |||
| + | ==Construct the LC circuit using a non-polar capacitor== | ||
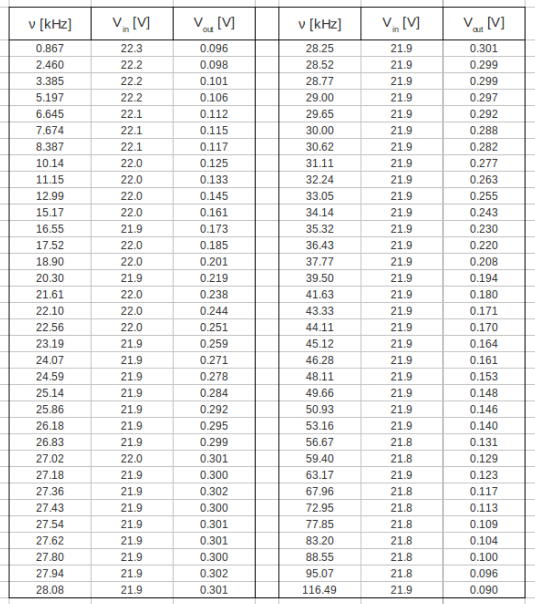
| + | ==Measure the Gain <math>\equiv \frac{V_{out}}{V_{in}}</math> as a function of frequency. (25 pnts)== | ||
| + | |||
| + | [[File:L5 LC table.png | 600 px]] | ||
| + | |||
| + | ==Compare the measured and theoretical values of the resonance frequency (<math>\omega_{L}</math>) (10 pnts)== | ||
| + | |||
| + | |||
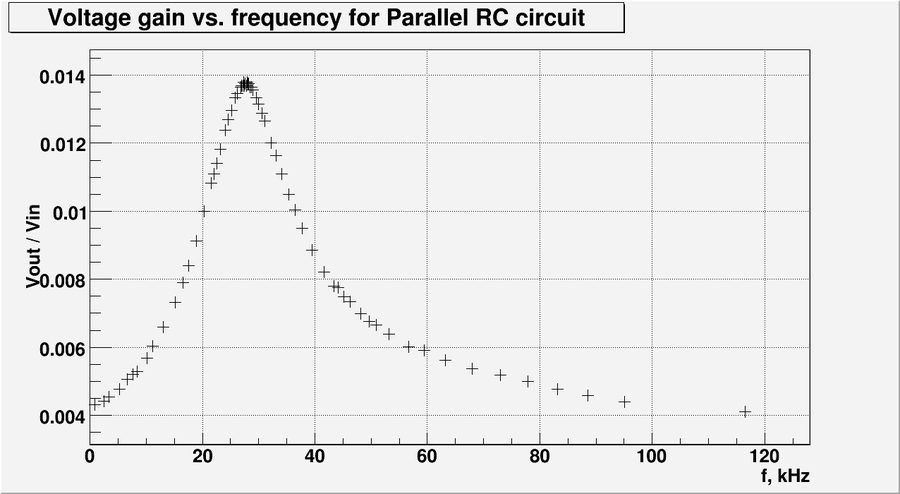
| + | Let's plot the data from table above: | ||
| + | |||
| + | [[File:L5 LC circuit.png | 900 px]] | ||
| + | |||
| + | |||
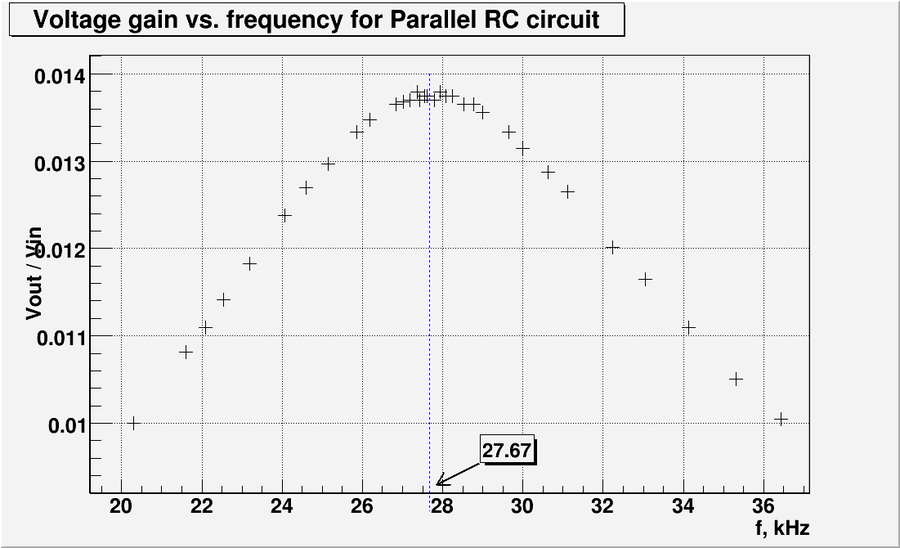
| + | And let's zoom the graph above at resonance frequency: | ||
| + | |||
| + | [[File:L5 LC zoom.png | 900 px]] | ||
| + | |||
| + | |||
| + | So the experimentally measured resonance frequency is: | ||
| + | |||
| + | <math>f = 27.7\ \mbox{kHz}</math> | ||
| + | |||
| + | And the predicted value of resonance frequency is: | ||
| + | |||
| + | <math>f = 27.4\ \mbox{kHz}</math> | ||
| + | |||
| + | The error is: | ||
| + | |||
| + | <math>Error = \left| \frac{f_{exp} - f_{theor}}{f_{theor}} \right| = \left| \frac{27.7 - 27.4}{27.4} \right|= 1.09\ %</math> | ||
| + | |||
| + | |||
| + | The error is small so I was lucky | ||
| + | |||
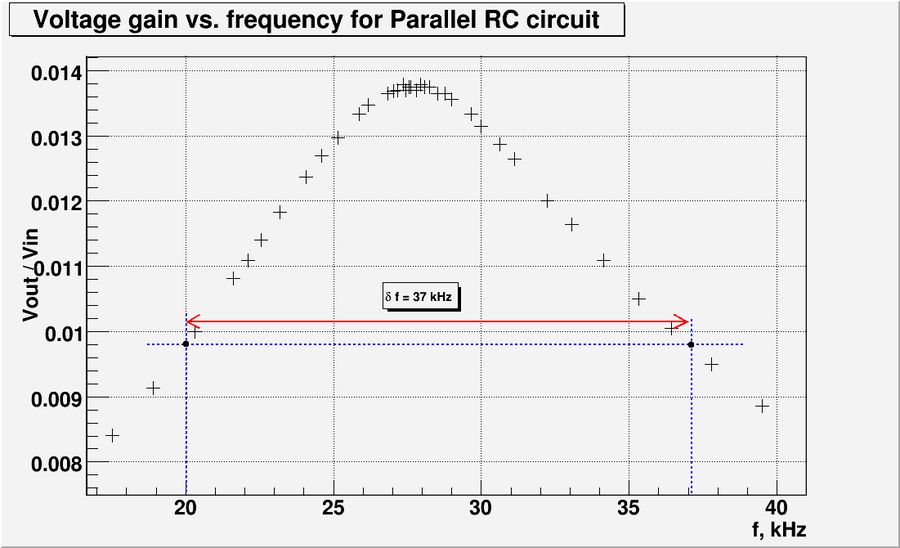
| + | ==Question. What is the bandwidth of the above circuit? (5 pnts)== | ||
| + | |||
| + | |||
| + | |||
| + | From the plot above we have <math>\left(\frac{V_{out}}{_{Vin}} \right)_{max} = 0.0138 </math> | ||
| + | |||
| + | The bandwidth defined as the width from <math>\omega_1</math> to <math>\omega_2</math> where the amplitude of signal drop down to <math>\frac{1}{\sqrt{2}}</math>. | ||
| + | |||
| + | At this point <math>\left(\frac{V_{out}}{V_{in}} \right) = \frac{0.0138}{\sqrt{2}} = 0.00976</math>. Let's plot this line and calculate the bandwidth. | ||
| + | |||
| + | |||
| + | [[File:L5 LC bandwidth.png | 900 px]] | ||
| + | |||
| + | |||
| + | So the bandwidth of the above circuit is | ||
| − | + | <math>\delta f = 37\ \mbox{kHz}</math> | |
| − | |||
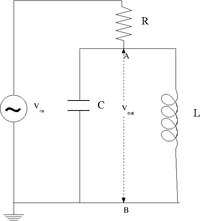
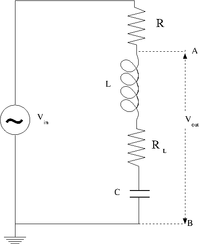
| − | =The | + | =The RLC cicuit= |
[[File:TF_EIM_Lab5_RLC.png| 200 px]] | [[File:TF_EIM_Lab5_RLC.png| 200 px]] | ||
| − | + | ==Design and construct a '''series''' LRC circuit== | |
| − | + | ==Measure and Graph the Gain as a function of the oscillating input voltage frequency. (25 pnts)== | |
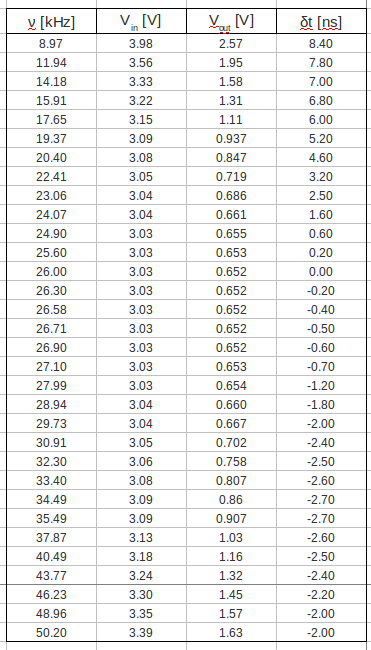
| + | |||
| + | :In the table below are my measurements for voltage gain and phase shift: | ||
| + | |||
| + | [[File:L5 RLC table.png | 400 px]] | ||
| + | |||
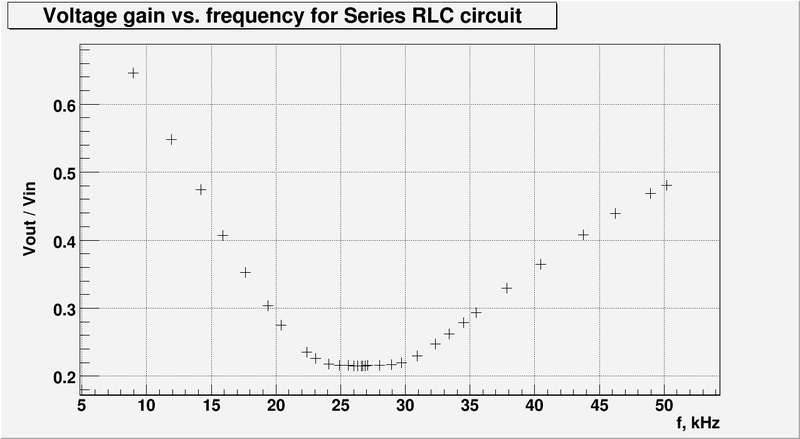
| + | :And let's graph the gain as a function of the input voltage frequency: | ||
| + | |||
| + | [[File:L5 RLC circuit.png | 800 px]] | ||
| + | |||
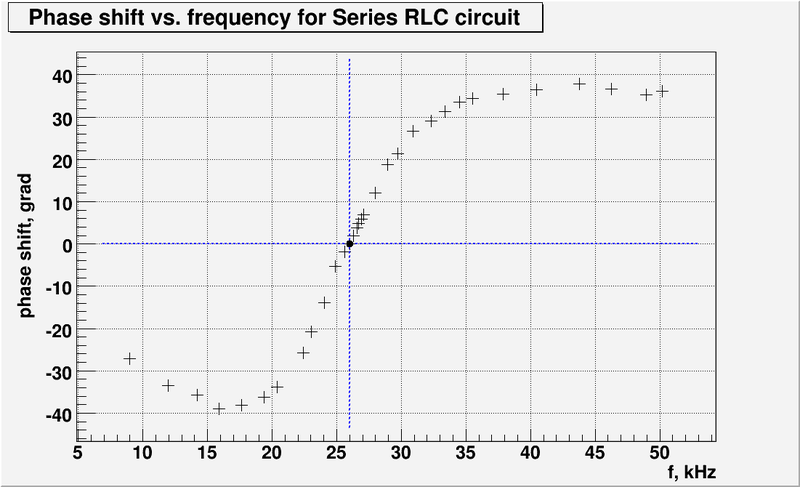
| + | ==Measure and Graph the Phase Shift as a function of the oscillating input voltage frequency. (25 pnts)== | ||
| + | |||
| + | :My phase shift measurements presented in the table above. And let's graph the phase shift as a function of the input voltage frequency: | ||
| + | |||
| + | [[File:L5 RLC circuit phase m1.png | 800 px]] | ||
| + | |||
| + | <br><br><br><br> | ||
| + | |||
==Questions== | ==Questions== | ||
| − | + | ===What is the current <math>I</math> at resonance? (5 pnts)=== | |
| − | + | ||
| + | [[File:Question1.png | 800 px]] | ||
| + | |||
| + | ===What is the current as <math>\nu \rightarrow \infty</math>? (5 pnts)=== | ||
| + | |||
| + | [[File:Question2.png | 400 px]] | ||
| + | |||
| + | |||
[[Forest_Electronic_Instrumentation_and_Measurement]] | [[Forest_Electronic_Instrumentation_and_Measurement]] | ||
| + | |||
| + | [https://wiki.iac.isu.edu/index.php/Electronics_RS Go Back to All Lab Reports] | ||
Latest revision as of 15:23, 7 February 2011
- LC Resonance circuits
The LC circuit
Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use = 10 - 100 , R = 1k
I choose the following values for and :
So the resonance frequency is
And
Construct the LC circuit using a non-polar capacitor
Measure the Gain as a function of frequency. (25 pnts)
Compare the measured and theoretical values of the resonance frequency () (10 pnts)
Let's plot the data from table above:
And let's zoom the graph above at resonance frequency:
So the experimentally measured resonance frequency is:
And the predicted value of resonance frequency is:
The error is:
The error is small so I was lucky
Question. What is the bandwidth of the above circuit? (5 pnts)
From the plot above we have
The bandwidth defined as the width from to where the amplitude of signal drop down to .
At this point . Let's plot this line and calculate the bandwidth.
So the bandwidth of the above circuit is
The RLC cicuit
Design and construct a series LRC circuit
Measure and Graph the Gain as a function of the oscillating input voltage frequency. (25 pnts)
- In the table below are my measurements for voltage gain and phase shift:
- And let's graph the gain as a function of the input voltage frequency:
Measure and Graph the Phase Shift as a function of the oscillating input voltage frequency. (25 pnts)
- My phase shift measurements presented in the table above. And let's graph the phase shift as a function of the input voltage frequency:
Questions
What is the current at resonance? (5 pnts)
What is the current as ? (5 pnts)