Difference between revisions of "Lab 4 RS"
| (7 intermediate revisions by the same user not shown) | |||
| Line 36: | Line 36: | ||
! scope="col" width="50" | <math>\frac{V_{out}}{V_{in}}</math> | ! scope="col" width="50" | <math>\frac{V_{out}}{V_{in}}</math> | ||
|- | |- | ||
| − | |0. | + | |0.5 ||12.4 ||0.48 ||0.039 |
|- | |- | ||
| − | |1.0 || || || | + | |1.0 ||11.0 ||0.88 ||0.080 |
|- | |- | ||
| − | |2.0 || || || | + | |2.0 ||8.0 ||1.3 ||0.162 |
|- | |- | ||
| − | |3.0 || || || | + | |3.0 ||6.0 ||1.5 ||0.250 |
|- | |- | ||
| − | |4.0 || || || | + | |4.0 ||4.9 ||1.6 ||0.326 |
|- | |- | ||
| − | |5.0 || || || | + | |5.0 ||4.2 ||1.7 ||0.405 |
|- | |- | ||
| − | |6.0 || || || | + | |6.0 ||3.7 ||1.7 ||0.459 |
|- | |- | ||
| − | |7.0 || || || | + | |7.0 ||3.2 ||1.7 ||0.531 |
|- | |- | ||
| − | |8.0 || || || | + | |8.0 ||3.0 ||1.75 ||0.583 |
|- | |- | ||
| − | |9.0 || || || | + | |9.0 ||2.85 ||1.70 ||0.596 |
|- | |- | ||
| − | |10.0 || || || | + | |10.0 ||2.60 ||1.70 ||0.654 |
|- | |- | ||
| − | |11.0 || || || | + | |11.0 ||2.50 ||1.70 ||0.680 |
|- | |- | ||
| − | |12.0 || || || | + | |12.0 ||2.35 ||1.70 ||0.723 |
|- | |- | ||
| − | | | + | |13.0 ||2.25 ||1.70 ||0.755 |
|- | |- | ||
| − | | | + | |14.0 ||2.20 ||1.70 ||0.772 |
|- | |- | ||
| − | | | + | |15.0 ||2.10 ||1.70 ||0.809 |
|- | |- | ||
| − | | | + | |20.0 ||2.00 ||1.75 ||0.875 |
|- | |- | ||
| − | | | + | |30.0 ||1.85 ||1.75 ||0.946 |
|- | |- | ||
| − | | | + | |50.0 ||1.82 ||1.78 ||0.978 |
|- | |- | ||
| − | | | + | |100.0 ||1.80 ||1.80 ||1.00 |
|} | |} | ||
| Line 80: | Line 80: | ||
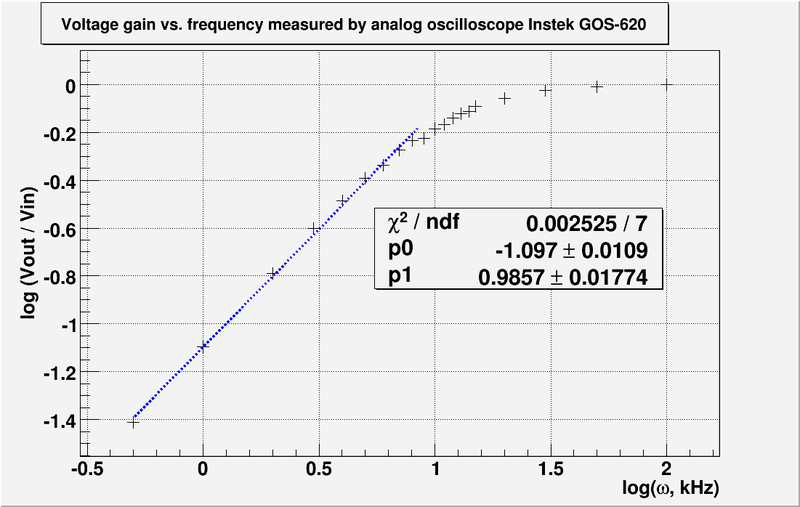
5. Graph the <math>\log \left(\frac{V_{out}}{V_{in}} \right)</math> -vs- <math>\log (\nu)</math> | 5. Graph the <math>\log \left(\frac{V_{out}}{V_{in}} \right)</math> -vs- <math>\log (\nu)</math> | ||
| − | [[File:L4 volt gain_analog.png | 800 px]] | + | [[File:L4 volt gain_analog m1.png | 800 px]] |
=phase shift (10 pnts)= | =phase shift (10 pnts)= | ||
| Line 93: | Line 93: | ||
Theoretical break frequency: <math>12.13\ \mbox{kHz}</math> | Theoretical break frequency: <math>12.13\ \mbox{kHz}</math> | ||
| − | The fit line equation from the plot above is <math>\ y=-1. | + | The fit line equation from the plot above is <math>\ y=-1.097+0.9857\cdot x</math>. |
From intersection point of line with x-axis we find: | From intersection point of line with x-axis we find: | ||
| − | :<math>\mbox{log}(f_{exper})=\frac{1. | + | :<math>\mbox{log}(f_{exper})=\frac{1.097}{0.9857} = 1.113</math> |
| − | :<math>f_{exp} = 10^{1. | + | :<math>f_{exp} = 10^{1.113} = 12.97\ \mbox{kHz} </math> |
The error is: | The error is: | ||
| − | <math>Error = \left| \frac{f_{exp} - f_{theor}}{f_{theor}} \right| = \left| \frac{ | + | <math>Error = \left| \frac{f_{exp} - f_{theor}}{f_{theor}} \right| = \left| \frac{12.97 - 12.13}{12.13} \right|= 6.92\ %</math> |
| − | |||
| − | |||
==2. Calculate and expression for <math>\frac{V_{out}}{ V_{in}}</math> as a function of <math>\nu</math>, <math>R</math>, and <math>C</math>.(5 pnts)== | ==2. Calculate and expression for <math>\frac{V_{out}}{ V_{in}}</math> as a function of <math>\nu</math>, <math>R</math>, and <math>C</math>.(5 pnts)== | ||
| Line 130: | Line 128: | ||
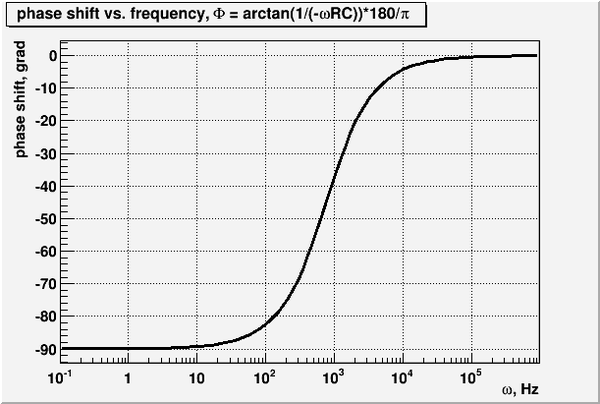
The theoretical phase shift is <math>\ \Theta_{theory}=\arctan\ \left (-\frac{1}{\omega R C}\right )</math> | The theoretical phase shift is <math>\ \Theta_{theory}=\arctan\ \left (-\frac{1}{\omega R C}\right )</math> | ||
| + | |||
| + | |||
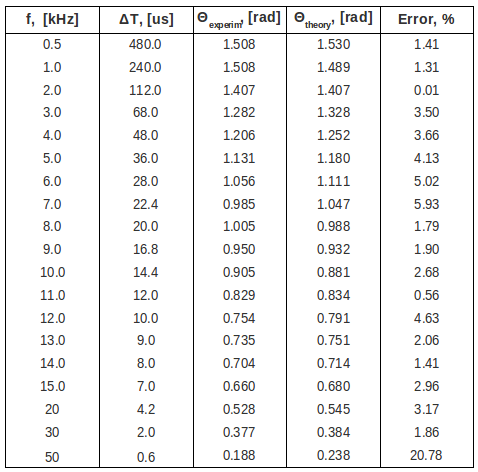
| + | [[File:l4_phase_table_m1.png | 600 px]] | ||
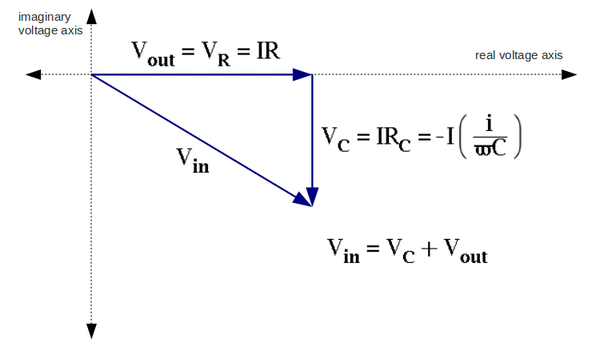
==4. Sketch the phasor diagram for <math>V_{in}</math>,<math> V_{out}</math>, <math>V_{R}</math>, and <math>V_{C}</math>. Put the current <math>I</math> along the real voltage axis. (30 pnts)== | ==4. Sketch the phasor diagram for <math>V_{in}</math>,<math> V_{out}</math>, <math>V_{R}</math>, and <math>V_{C}</math>. Put the current <math>I</math> along the real voltage axis. (30 pnts)== | ||
| Line 138: | Line 139: | ||
Because a DC circuit doesn't have any oscillation there are no any phase shift. | Because a DC circuit doesn't have any oscillation there are no any phase shift. | ||
| + | |||
| + | For a very high frequency input the phase shift is 0 (see plot in question 6) | ||
==6. Calculate and expression for the phase shift <math>\theta</math> as a function of <math>\nu</math>, <math>R</math>, <math>C</math> and graph <math>\theta</math> -vs <math>\nu</math>. (20 pnts)== | ==6. Calculate and expression for the phase shift <math>\theta</math> as a function of <math>\nu</math>, <math>R</math>, <math>C</math> and graph <math>\theta</math> -vs <math>\nu</math>. (20 pnts)== | ||
Latest revision as of 22:34, 3 February 2011
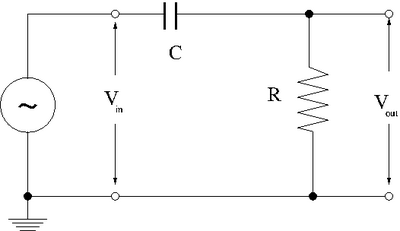
- RC High-pass filter
1-50 kHz filter (20 pnts)
1. Design a high-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter's attenuation of the AC signal goes to 0(not passed). For a High pass filter, AC signals with a frequency below the 1-50 kHz range will be attenuated .
- To design low-pass RC filter I had:
So
2. Now construct the circuit using a non-polar capacitor.
3. Use a sinusoidal variable frequency oscillator to provide an input voltage to your filter.
4. Measure the input and output voltages for at least 8 different frequencies which span the frequency range from 1 Hz to 1 MHz.
| 0.5 | 12.4 | 0.48 | 0.039 |
| 1.0 | 11.0 | 0.88 | 0.080 |
| 2.0 | 8.0 | 1.3 | 0.162 |
| 3.0 | 6.0 | 1.5 | 0.250 |
| 4.0 | 4.9 | 1.6 | 0.326 |
| 5.0 | 4.2 | 1.7 | 0.405 |
| 6.0 | 3.7 | 1.7 | 0.459 |
| 7.0 | 3.2 | 1.7 | 0.531 |
| 8.0 | 3.0 | 1.75 | 0.583 |
| 9.0 | 2.85 | 1.70 | 0.596 |
| 10.0 | 2.60 | 1.70 | 0.654 |
| 11.0 | 2.50 | 1.70 | 0.680 |
| 12.0 | 2.35 | 1.70 | 0.723 |
| 13.0 | 2.25 | 1.70 | 0.755 |
| 14.0 | 2.20 | 1.70 | 0.772 |
| 15.0 | 2.10 | 1.70 | 0.809 |
| 20.0 | 2.00 | 1.75 | 0.875 |
| 30.0 | 1.85 | 1.75 | 0.946 |
| 50.0 | 1.82 | 1.78 | 0.978 |
| 100.0 | 1.80 | 1.80 | 1.00 |
5. Graph the -vs-
phase shift (10 pnts)
- measure the phase shift between and as a function of frequency . Hint: you could use as an external trigger and measure the time until reaches a max on the scope .
See question 3 about my phase shift measurements
Questions
1. Compare the theoretical and experimentally measured break frequencies. (5 pnts)
Theoretical break frequency:
The fit line equation from the plot above is . From intersection point of line with x-axis we find:
The error is:
2. Calculate and expression for as a function of , , and .(5 pnts)
We have:
Dividing second equation into first one we get the voltage gain:
And we are need the real part:
3. Compare the theoretical and experimental value for the phase shift . (5 pnts)
The experimental phase shift is
The theoretical phase shift is
4. Sketch the phasor diagram for ,, , and . Put the current along the real voltage axis. (30 pnts)
5. What is the phase shift for a DC input and a very-high frequency input?(5 pnts)
Because a DC circuit doesn't have any oscillation there are no any phase shift.
For a very high frequency input the phase shift is 0 (see plot in question 6)
6. Calculate and expression for the phase shift as a function of , , and graph -vs . (20 pnts)
From the phasor diagram above (question 4) the angle between vectors and given by
Forest_Electronic_Instrumentation_and_Measurement Go Back to All Lab Reports