Difference between revisions of "TF EIMLab1 Writeup"

From New IAC Wiki
Jump to navigation Jump to search
 
(11 intermediate revisions by the same user not shown)
Line 65: Line 65:
 
|Variable ||Measured Value|| Predicted Value|| % Difference
 
|Variable ||Measured Value|| Predicted Value|| % Difference
 
|-
 
|-
−
| <math>V_B</math> || 103.5 mV  || 156 || 50%
+
| <math>V_B</math> || 103.5 +/- 50 mV  || 156 || 50%
 
|-
 
|-
 
| <math>I_1</math> || 20.4 mA  ||22 || 7%
 
| <math>I_1</math> || 20.4 mA  ||22 || 7%
Line 77: Line 77:
  
 
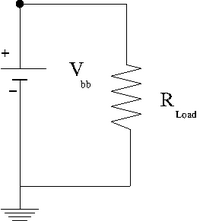
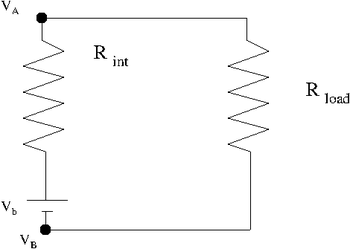
Measure the internal resistance of your power source by graphing the potential difference on the x-axis and the current on the y-axis for several values of the resistance <math>R_L</math> shown in the circuit below.  Begin with <math>R_L = 1k\Omega</math> and then decrease it by a factor of 5 for each subsequent measurement.  You can use a volt meter to measure the current and potential difference.
 
Measure the internal resistance of your power source by graphing the potential difference on the x-axis and the current on the y-axis for several values of the resistance <math>R_L</math> shown in the circuit below.  Begin with <math>R_L = 1k\Omega</math> and then decrease it by a factor of 5 for each subsequent measurement.  You can use a volt meter to measure the current and potential difference.
 +
 +
 +
[[File:TF_EIM_Lab1a_fig.png | 200px]][[File:TF_EIM_Lab1b_fig.png | 350px]]
  
  
 
{| border="3"  cellpadding="20" cellspacing="0"
 
{| border="3"  cellpadding="20" cellspacing="0"
−
| R (<math>\Omega</math>) || V (mv) || I (mA)
+
| R_{Load} (<math>\Omega</math>) || V (Volts)|| I (mA)
 +
|-
 +
| 10|| 1.42 <math>\pm</math> 0.06 || 118 <math>\pm</math> 3
 +
|-
 +
| 93|| 1.55<math> \pm</math> 0.01 || 16.15 <math>\pm</math> 0.05
 +
|-
 +
|990 || 1.575 <math>\pm</math> 0.005 || 1.54 <math>\pm</math> 0.04
 +
|-
 +
|10110 || 1.579 <math>\pm</math> 0.005 || 0.146 <math>\pm</math> 0.005
 
|-
 
|-
−
| || ||  
+
| 15060|| 1.579 <math>\pm</math> 0.005 || 0.101 <math>\pm</math> 0.003
 
|}
 
|}
  
 +
<math>V_A - V_B = IR_{Load} = V_{bb} - I R_{int}</math>
 +
 +
<math>(V_A - V_B) = - R_{int} I +  V_{bb}</math>
 +
 +
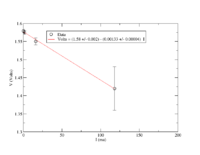
<math>y = mx+b \Rightarrow R_{int} =</math> slope of V-vs- I plot
 +
 +
[[File:Lab1b_TF_EIM.png | 200 px]]
 +
 +
;Since the current is in mA the resistance must be in kOhms in order to get volts.
 +
 +
:<math>R_{int} = 1.33 \pm 0.04 \Omega</math>
 +
 +
Book suggests 1.5 flashlight battery could have an internal resistance of 0.5 Ohms.
  
 
Below I set R= 95 <math>\Omega</math>  and changed V
 
Below I set R= 95 <math>\Omega</math>  and changed V

Latest revision as of 17:40, 20 January 2015

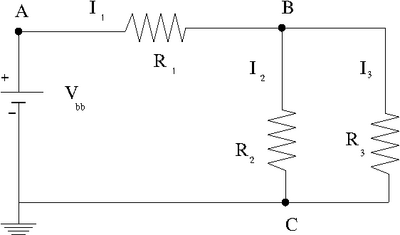
Kirchoff's Law (50 pnts)

Construct the circuit below

TF EIM Lab1.png


Enter the values of the DC voltage and Resisters that you used.

Use a voltmeter to measure the potential difference and resistances.

Variable Measured Value
[math]V_A [/math] 20 Volts
[math]R_1[/math] 902 [math]\Omega[/math]
[math]R_2[/math] 10.2 [math]\Omega[/math]
[math]R_3[/math] 10.6 [math]\Omega[/math]

Enter the measured and predicted quantities in the table below

Given [math]V_A[/math] and the values of all resistors, use Kirchoff's laws to predict

a.) Predict the value of [math]V_B[/math]

[math]V_A - I_1R_1 = V_b [/math]

I_1 =?

Kirchoff's Loop theorem (Voltage Law)

[math]V_A -I_1(R_1+R_{tot}) = 0[/math] where R[math]_{tot}[/math] =resistance for [math]R_2[/math] and [math]R_3[/math] in series.

[math]R_{tot} = \frac{1}{\frac{1}{R_2} + \frac{1}{R_3}} = 5.2 \Omega[/math]

[math]I_1 = \frac{V_A}{R_1+R_{tot}} = \frac{ 20 \mbox{Volts}}{902 \Omega + 5.2 \Omega} = 22 \mbox{mA}[/math]


[math]V_b = V_A - I_1 R_1 = 20 - 0.022 \times 902 = 156[/math] mV

b.) Predict the values of the three currents.

[math]I_1 = I_2 + I_3[/math]

I[math]_2 R_2 - I_3 R_3 = 0[/math]

2 equations and 2 unkowns

[math]I_3 = \frac{I_1}{\frac{R_3}{R_2} +1} = \frac{22 mV}{\frac{10.6}{10.2}+1} = 10.8[/math] mA

[math]I_2 = I_1 - I_3 = 22 - 10.8 = 11.2[/math] mA

c.) compare your predictions and measurements by filling in the table below.

Variable Measured Value Predicted Value % Difference
[math]V_B[/math] 103.5 +/- 50 mV 156 50%
[math]I_1[/math] 20.4 mA 22 7%
[math]I_2[/math] 9.5 mA 11.2 18%
[math]I_3[/math] 9.0 mA 10.8 20%

Internal resistance (30 pnts)

Measure the internal resistance of your power source by graphing the potential difference on the x-axis and the current on the y-axis for several values of the resistance [math]R_L[/math] shown in the circuit below. Begin with [math]R_L = 1k\Omega[/math] and then decrease it by a factor of 5 for each subsequent measurement. You can use a volt meter to measure the current and potential difference.


TF EIM Lab1a fig.pngTF EIM Lab1b fig.png


R_{Load} ([math]\Omega[/math]) V (Volts) I (mA)
10 1.42 [math]\pm[/math] 0.06 118 [math]\pm[/math] 3
93 1.55[math] \pm[/math] 0.01 16.15 [math]\pm[/math] 0.05
990 1.575 [math]\pm[/math] 0.005 1.54 [math]\pm[/math] 0.04
10110 1.579 [math]\pm[/math] 0.005 0.146 [math]\pm[/math] 0.005
15060 1.579 [math]\pm[/math] 0.005 0.101 [math]\pm[/math] 0.003

[math]V_A - V_B = IR_{Load} = V_{bb} - I R_{int}[/math]

[math](V_A - V_B) = - R_{int} I + V_{bb}[/math]

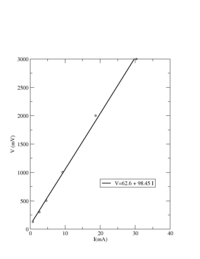
[math]y = mx+b \Rightarrow R_{int} =[/math] slope of V-vs- I plot

Lab1b TF EIM.png

Since the current is in mA the resistance must be in kOhms in order to get volts.
[math]R_{int} = 1.33 \pm 0.04 \Omega[/math]

Book suggests 1.5 flashlight battery could have an internal resistance of 0.5 Ohms.

Below I set R= 95 [math]\Omega[/math] and changed V

V (mv) I (mA)
126.1 0.79
300 2.64
500 4.62
1000 9.29
2000 18.78
3000 30.4

Now lets try to fix V and change R


Lab1a TF EIM.png

Questions (20 pnts)

  1. What conservation law is involved in Kirchoff's Loop Theorem?
  2. What does the slope in the internal resistance plot above represent?


TF_EIM_LabWriteups

Retrieved from "https://wiki.iac.isu.edu/index.php?title=TF_EIMLab1_Writeup&oldid=98951"