Difference between revisions of "Lab 3 TF EIM"
Jump to navigation
Jump to search
| (29 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | RC Low-pass filter | + | ;RC Low-pass filter |
| − | = 1-50 kHz filter= | + | = 1-50 kHz filter (20 pnts)= |
| − | + | 1.) Design a low-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter starts to attenuate the AC signal. For a Low pass filter, AC signals with a frequency above 1-50 kHz will start to be attenuated (not passed). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | =phase shift= | + | Enter your values for<math> R, C,</math> and <math>\omega</math> |
| − | #measure the phase shift between <math>V_{in}</math> and <math>V_{out}</math> | + | {| border="3" cellpadding="20" cellspacing="0" |
| + | |R||C || <math> \omega</math> || <math>\nu</math> | ||
| + | |- | ||
| + | | || || || | ||
| + | |} | ||
| + | |||
| + | |||
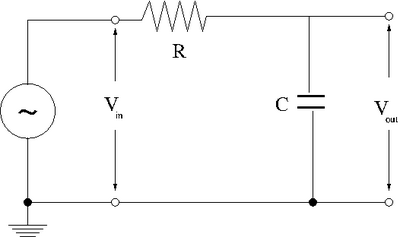
| + | 2.)Now construct the circuit using a non-polar capacitor. | ||
| + | |||
| + | [[File:TF_EIM_Lab3.png | 400 px]] | ||
| + | |||
| + | 3.)use a sinusoidal variable frequency oscillator to provide an input voltage to your filter. | ||
| + | |||
| + | 4.)Measure the input <math>(V_{in})</math> and output <math>(V_{out})</math> voltages for at least 8 different frequencies<math> (\nu)</math> which span the frequency range from 1 Hz to 1 MHz. | ||
| + | |||
| + | |||
| + | |||
| + | {| border="3" cellpadding="20" cellspacing="0" | ||
| + | |<math>\nu</math> ||<math>V_{in}</math> || <math>V_{out}</math> || <math>\frac{V_{out}}{V_{in}}</math> | ||
| + | |- | ||
| + | | Hz || Volts || Volts || | ||
| + | |- | ||
| + | | || || || | ||
| + | |- | ||
| + | | || || || | ||
| + | |- | ||
| + | | || || || | ||
| + | |- | ||
| + | | || || || | ||
| + | |- | ||
| + | | || || || | ||
| + | |- | ||
| + | | || || || | ||
| + | |- | ||
| + | | || || || | ||
| + | |- | ||
| + | | || || || | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | 5.) Graph the <math>\log \left(\frac{V_{out}}{V_{in}} \right)</math> -vs- <math>\log (\nu)</math> | ||
| + | |||
| + | =phase shift (10 pnts)= | ||
| + | #measure the phase shift between <math>V_{in}</math> and <math>V_{out}</math> as a function of frequency <math>\nu</math>. Hint: you could use<math> V_{in}</math> as an external trigger and measure the time until <math>V_{out}</math> reaches a max on the scope <math>(\sin(\omega t + \phi) = \sin\left ( \omega\left [t + \frac{\phi}{\omega}\right]\right )= \sin\left ( \omega\left [t + \delta t \right] \right ))</math>. | ||
=Questions= | =Questions= | ||
| − | # | + | #Compare the theoretical and experimentally measured break frequencies. (5 pnts) |
| − | #Calculate | + | #Calculate an expression for <math>\frac{V_{out}}{ V_{in}}</math> as a function of <math>\nu</math>, <math>R</math>, and <math>C</math>. The Gain is defined as the ratio of <math>V_{out}</math> to <math>V_{in}</math>.(5 pnts) |
| − | + | #Sketch the phasor diagram for <math>V_{in}</math>,<math> V_{out}</math>, <math>V_{R}</math>, and <math>V_{C}</math>.(30 pnts) | |
| − | #Sketch the phasor diagram for <math>V_{in}</math>,<math> V_{out}</math>, <math>V_{R}</math>, and <math>V_{C}</math>. | + | #Calculate an expression for the phase shift <math>\theta</math> as a function of <math>\nu</math>, <math>R</math>, <math>C</math> and graph <math>\theta</math> -vs <math>\nu</math>. (20 pnts) |
| − | # | + | #Compare the theoretical and experimental value for the phase shift <math>\theta</math>. (5 pnts) |
| − | + | # what is the phase shift <math>\theta</math> for a DC input (the limit as frequency goes to zero) and a very-high frequency input?(5 pnts) | |
| + | |||
| + | |||
| + | [[Forest_Electronic_Instrumentation_and_Measurement]] | ||
Latest revision as of 17:59, 2 February 2015
- RC Low-pass filter
1-50 kHz filter (20 pnts)
1.) Design a low-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter starts to attenuate the AC signal. For a Low pass filter, AC signals with a frequency above 1-50 kHz will start to be attenuated (not passed).
Enter your values for and
| R | C | ||
2.)Now construct the circuit using a non-polar capacitor.
3.)use a sinusoidal variable frequency oscillator to provide an input voltage to your filter.
4.)Measure the input and output voltages for at least 8 different frequencies which span the frequency range from 1 Hz to 1 MHz.
| Hz | Volts | Volts | |
5.) Graph the -vs-
phase shift (10 pnts)
- measure the phase shift between and as a function of frequency . Hint: you could use as an external trigger and measure the time until reaches a max on the scope .
Questions
- Compare the theoretical and experimentally measured break frequencies. (5 pnts)
- Calculate an expression for as a function of , , and . The Gain is defined as the ratio of to .(5 pnts)
- Sketch the phasor diagram for ,, , and .(30 pnts)
- Calculate an expression for the phase shift as a function of , , and graph -vs . (20 pnts)
- Compare the theoretical and experimental value for the phase shift . (5 pnts)
- what is the phase shift for a DC input (the limit as frequency goes to zero) and a very-high frequency input?(5 pnts)