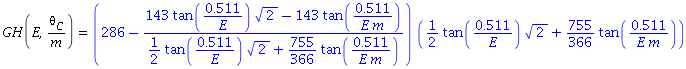Difference between revisions of "Minimum accelerator energy to run experiment"

From New IAC Wiki
Jump to navigation Jump to search
 
(46 intermediate revisions by one other user not shown)
Line 1: Line 1:
−
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back]
+
[https://wiki.iac.isu.edu/index.php/Roman_calculation Go Back]
  
 
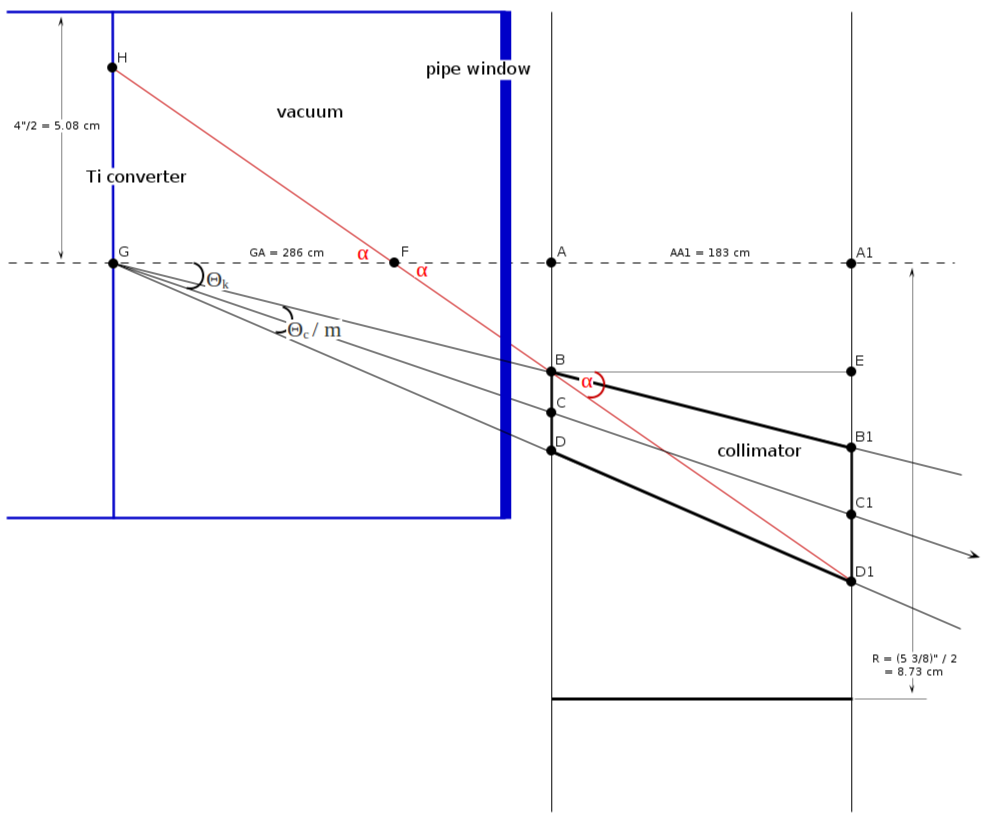
=general setup=
 
=general setup=
  
−
[[File:minimum_energy_condition.png|600px]]
+
[[File:minimum_energy_condition.png]]
  
−
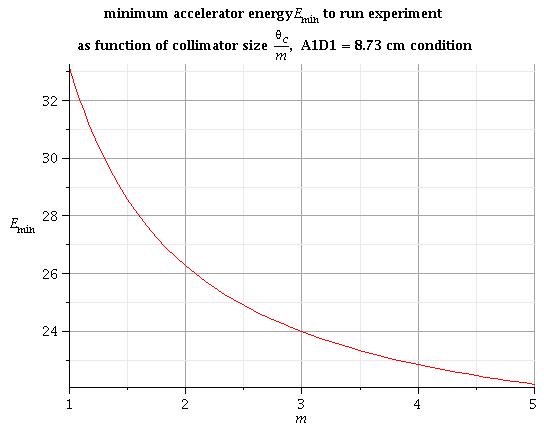
= fitting the collimator size into the hole in the concrete wall=
+
= fitting the collimator size into the hole through the concrete wall=
  
 
I can express the distance <math>A_1D_1</math> as function of collimator size <math>\Theta_C/m</math> and electron beam energy E:
 
I can express the distance <math>A_1D_1</math> as function of collimator size <math>\Theta_C/m</math> and electron beam energy E:
 
   
 
   
−
  <math>A_1D_1(E,\ \Theta_C/m) = \frac{469}{2}\tan\left(\frac{0.511}{E}\right)
+
  [[File:formula_cond11.png]]
−
                              + \frac{469}{\sqrt{2}}\tan\left(\frac{1}{m}\frac{0.511}{E}\right)</math>
 
  
−
The minimum energy of accelerator (MeV) is limited by fitting the collimator size <math>r_2</math> into the hole R = 8.73 cm:
+
To fit the collimator size into the hole through the concrete wall with radius R = 8.73 cm we need to solve equation:
  
−
<math>x_2 + r_2 = R</math>
+
<math>A_1D_1(E,\ \Theta_C/m) = 8.73\ cm</math>
  
−
1) Assuming the collimator diameter is <math>\Theta_C</math>:
+
1) some solutions of this equation for different collimator sizes m are:
  
−
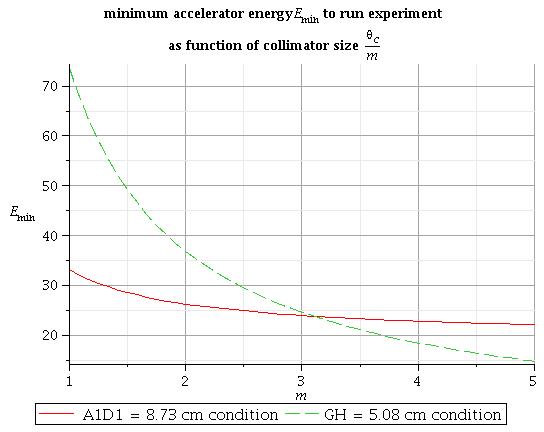
  <math>\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
+
  <math>m = 1 \Rightarrow E_{min} = 33.1\ MeV  </math><br>
−
      \frac{1}{2}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 33.1\ MeV  </math>
+
<math>m = 2 \Rightarrow E_{min} = 26.3\ MeV  </math><br>
 +
<math>m = 4 \Rightarrow E_{min} = 22.8\ MeV  </math><br>
  
−
2) Assuming the collimator diameter is <math>\Theta_C/2</math>:
+
2) in general for arbitrary collimator size m the solutions are:
  
−
<math>\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
+
[[File:energy_condition1.jpeg]]
−
      \frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{2}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 26.3\ MeV  </math>
 
  
−
3) Assuming the collimator diameter is <math>\Theta_C/4</math>:
+
All energies above this line is good to run experiment for condition above
  
−
<math>\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
+
=critical collimator line condition=
−
      \frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{4}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 22.8\ MeV  </math>
 
  
−
4) for arbitrary collimator size <math>\Theta_C/2</math>:
+
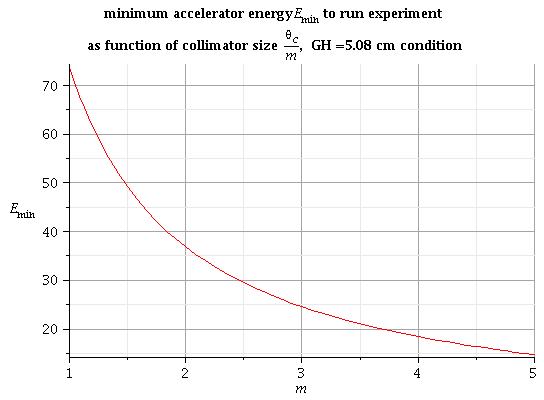
Also I can express the distance <math>GH</math> as function of collimator size <math>\Theta_C/m</math> and electron beam energy E:
−
 
+
−
[[File:plot_energy_collimatorsize.jpeg]]
+
[[File:formula_cond21.png]]
−
 
+
−
All energy under this line is good to run experiment for condition above
+
If I would like that nothing hitting the 4" box to go through the collimator I need to solve equation:
−
 
 
−
=GH = 5.08 cm condition=
 
−
 
 
−
1) assuming the collimator diameter is <math>\Theta_C</math>
 
−
 
 
−
<math> E_{min} = 73.7\ MeV  </math>
 
−
 
 
−
2) assuming the collimator diameter is <math>\Theta_C/2</math>
 
  
−
  <math> E_{min} = 36.9\ MeV  </math>
+
  <math>GH(E,\ \Theta_C/m) = 5.08\ cm</math>
  
−
3) assuming the collimator diameter is <math>\Theta_C/4</math>
+
1) some solutions of this equation for different collimator sizes m are:
  
−
  <math> E_{min} = 18.4\ MeV  </math>
+
  <math>m = 1 \Rightarrow E_{min} = 73.7\ MeV  </math><br>
 +
<math>m = 2 \Rightarrow E_{min} = 36.9\ MeV  </math><br>
 +
<math>m = 4 \Rightarrow E_{min} = 18.4\ MeV  </math><br>
  
−
4) for arbitrary collimator size <math>\Theta_C/m</math>:
+
2) in general for arbitrary collimator size m the solutions are:
  
−
[[File:plot_energy_F1A.jpeg]]
+
[[File:energy_condition2.jpeg]]
  
−
All energy under this line is good to run experiment for condition above
+
All energies above this line is good to run experiment for condition above
  
−
=both conditions above are together=
+
=both solutions are together=
  
−
[[File:plot_energy_bothcondition.jpeg]]
+
[[File:energy_condition12.jpeg]]
  
−
All energy under this linse is good to run experiment for both conditions above
+
All energies above this lines is good to run experiment for both conditions above
  
  
  
 
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back]
 
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back]

Latest revision as of 19:03, 24 May 2012

Go Back

general setup

Minimum energy condition.png

fitting the collimator size into the hole through the concrete wall

I can express the distance [math]A_1D_1[/math] as function of collimator size [math]\Theta_C/m[/math] and electron beam energy E: 

Formula cond11.png

To fit the collimator size into the hole through the concrete wall with radius R = 8.73 cm we need to solve equation: 

[math]A_1D_1(E,\ \Theta_C/m) = 8.73\ cm[/math]

1) some solutions of this equation for different collimator sizes m are: 

[math]m = 1 \Rightarrow E_{min} = 33.1\ MeV  [/math]

[math]m = 2 \Rightarrow E_{min} = 26.3\ MeV  [/math]

[math]m = 4 \Rightarrow E_{min} = 22.8\ MeV  [/math]

2) in general for arbitrary collimator size m the solutions are:

Energy condition1.jpeg

All energies above this line is good to run experiment for condition above

critical collimator line condition

Also I can express the distance [math]GH[/math] as function of collimator size [math]\Theta_C/m[/math] and electron beam energy E: 

Formula cond21.png

If I would like that nothing hitting the 4" box to go through the collimator I need to solve equation: 

[math]GH(E,\ \Theta_C/m) = 5.08\ cm[/math]

1) some solutions of this equation for different collimator sizes m are: 

[math]m = 1 \Rightarrow E_{min} = 73.7\ MeV  [/math]

[math]m = 2 \Rightarrow E_{min} = 36.9\ MeV  [/math]

[math]m = 4 \Rightarrow E_{min} = 18.4\ MeV  [/math]

2) in general for arbitrary collimator size m the solutions are:

Energy condition2.jpeg

All energies above this line is good to run experiment for condition above

both solutions are together

Energy condition12.jpeg

All energies above this lines is good to run experiment for both conditions above


Go Back

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Minimum_accelerator_energy_to_run_experiment&oldid=74568"