Difference between revisions of "Converter Temperture"
(Created page with '[http://wiki.iac.isu.edu/index.php/HRRL Go Back] =Calculating Radiators Equilibrium Temperature= ==1.Calculating number of particles per second == We have electron beam of: F...') |
|||
| (33 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | [[Positrons]] |
| Line 9: | Line 9: | ||
Frequency: f=1000Hz | Frequency: f=1000Hz | ||
| − | Peak current: I= | + | Peak current: I=10~mAmp=0.01 Amp |
| − | Pulse width: | + | Pulse width: <math> \Delta t= 50~ns=5 \times10^{-8}</math> seconds |
So, how many electrons we have in each second? | So, how many electrons we have in each second? | ||
| Line 17: | Line 17: | ||
By Q=It, we have | By Q=It, we have | ||
| − | |||
| − | Where | + | <math> N \times e=f \times I \times \Delta t </math> |
| + | |||
| + | |||
| + | Where N is the total electron numbers hits target per second, e is electron charge and f, I and ∆t are given above. | ||
So | So | ||
| − | |||
| − | So, we have around 3.12075 | + | |
| + | <math> N = \frac {f \times I \times \Delta t}{e} = \frac {1000 \times 0.01 \times 5\times10^{-8} }{1.6 \times 10^{-19}} =3.12075 \times 10^{12 }</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | So, we have around <math> 3.12075 \times 10^{12 }</math> electrons hit radiator per second. | ||
==2.Calculating Energy deposited per second== | ==2.Calculating Energy deposited per second== | ||
| Line 32: | Line 39: | ||
To find energy deposited by each electron, we need to use formula | To find energy deposited by each electron, we need to use formula | ||
| − | <math> E_{dep | + | <math> E_{dep~one}={(\frac{dE}{dx})}_{coll}\times t </math> |
| − | Where is <math> E_{dep one}</math> is energy deposited by one electron, <math>(dE | + | Where is <math> E_{dep~one} </math> is energy deposited by one electron, <math> {(\frac{dE}{dx})}_{coll} </math> is mean energy loss (also stopping power) by collision of electron and <math> t </math> is thickness of the radiator. |
Actually, energy loss of electron comes from two parts: the emission of electromagnetic radiation arising from scattering in the electric field of a nucleus (bremsstrahlung) and collisional energy loss when passing through matter. But bremsstrahlung will not contribute to the temperature, since it is radiation. | Actually, energy loss of electron comes from two parts: the emission of electromagnetic radiation arising from scattering in the electric field of a nucleus (bremsstrahlung) and collisional energy loss when passing through matter. But bremsstrahlung will not contribute to the temperature, since it is radiation. | ||
| Line 50: | Line 57: | ||
|Elements | |Elements | ||
|Radiation Lengths <math> (g/cm^{2} )</math> | |Radiation Lengths <math> (g/cm^{2} )</math> | ||
| − | |||
| − | |||
|- | |- | ||
|W || 6.76 | |W || 6.76 | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
|}<br> | |}<br> | ||
| Line 73: | Line 75: | ||
|<math>E_{dep/s}</math> (MeV/s) | |<math>E_{dep/s}</math> (MeV/s) | ||
|<math>E_{dep/s}</math> (J/s) | |<math>E_{dep/s}</math> (J/s) | ||
| − | |||
| − | |||
|- | |- | ||
|W ||1.247 ||0.00676 ||0.00842972 ||<math>2.63*10^{10}</math> ||<math>4.21*10^{-3}</math> | |W ||1.247 ||0.00676 ||0.00842972 ||<math>2.63*10^{10}</math> ||<math>4.21*10^{-3}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
|} | |} | ||
| Line 111: | Line 107: | ||
|Stefan-Boltzmann Constant | |Stefan-Boltzmann Constant | ||
|<math>T_{equ}</math> (K) | |<math>T_{equ}</math> (K) | ||
| − | |||
| − | |||
|- | |- | ||
|W ||0.002 ||0.00000628 ||<math>5.6704*10^{-8}</math> ||329.8 | |W ||0.002 ||0.00000628 ||<math>5.6704*10^{-8}</math> ||329.8 | ||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
|} | |} | ||
| Line 126: | Line 116: | ||
We can calculate separately for Al, W and Ti for different thickness and different beam spot diameter. Following tables are temperature calculation for Al, W Ti and Fe in thickness of 0.001, 0.005 and 0.01 times of Radiation Length, in beam spot of diameter of 2, 4, 6, 8, 10 mm. | We can calculate separately for Al, W and Ti for different thickness and different beam spot diameter. Following tables are temperature calculation for Al, W Ti and Fe in thickness of 0.001, 0.005 and 0.01 times of Radiation Length, in beam spot of diameter of 2, 4, 6, 8, 10 mm. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===W=== | ===W=== | ||
| Line 173: | Line 140: | ||
[[Image:Equilibrium Temperature for W.jpg]] | [[Image:Equilibrium Temperature for W.jpg]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==5. Results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width ) == | ==5. Results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width ) == | ||
Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of 0.00001, 0.0005 and 0.0001 times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm. | Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of 0.00001, 0.0005 and 0.0001 times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 274: | Line 168: | ||
[[Image:W_2.jpg|down|800px]] | [[Image:W_2.jpg|down|800px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==6. More results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width for Θ₀ = 0.2,0.4,0.6 dgrees) == | ==6. More results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width for Θ₀ = 0.2,0.4,0.6 dgrees) == | ||
| Line 330: | Line 173: | ||
Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of <math>3.9*10^{-5}</math> (Θ₀ = <math>0.2^{o}</math>), <math>1.35*10^{-4}</math>(Θ₀= <math>0.4^{o}</math>) and <math>2.8*10^{-4}</math>(Θ₀ = <math>0.6^{o}</math>) times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm. | Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of <math>3.9*10^{-5}</math> (Θ₀ = <math>0.2^{o}</math>), <math>1.35*10^{-4}</math>(Θ₀= <math>0.4^{o}</math>) and <math>2.8*10^{-4}</math>(Θ₀ = <math>0.6^{o}</math>) times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===W=== | ===W=== | ||
| Line 375: | Line 197: | ||
[[Image:W_3.jpg|down|800px]] | [[Image:W_3.jpg|down|800px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [ | + | [[Positrons]]Go Back |
Latest revision as of 03:32, 8 June 2010
Calculating Radiators Equilibrium Temperature
1.Calculating number of particles per second
We have electron beam of:
Frequency: f=1000Hz
Peak current: I=10~mAmp=0.01 Amp
Pulse width: seconds
So, how many electrons we have in each second?
By Q=It, we have
Where N is the total electron numbers hits target per second, e is electron charge and f, I and ∆t are given above.
So
So, we have around electrons hit radiator per second.
2.Calculating Energy deposited per second
If we find the energy deposited by each electron and multiply to the total number of electrons in each second, we will find the total energy per second deposited in radiator.
To find energy deposited by each electron, we need to use formula
Where is is energy deposited by one electron, is mean energy loss (also stopping power) by collision of electron and is thickness of the radiator.
Actually, energy loss of electron comes from two parts: the emission of electromagnetic radiation arising from scattering in the electric field of a nucleus (bremsstrahlung) and collisional energy loss when passing through matter. But bremsstrahlung will not contribute to the temperature, since it is radiation.
Stopping power can be found from nuclear data tables and thickness is 0.001 times of radiation length. From Particle Data group we got radiation length and average total stopping powers around 15MeV for electrons in these materials from National Institute of Standards and Technology
Table of Radiation Lengths
Note:These data is from Particle Data group,Link: [1].
| Elements | Radiation Lengths |
| W | 6.76 |
Table of energy calculations
For the thickness of 0.001 Radiation Length (0.0001RL) of radiators. Note: is from National Institute of Standards and Technology. Link: [[2]])
| Elements | t( ) | (MeV) | (MeV/s) | (J/s) | |
| W | 1.247 | 0.00676 | 0.00842972 |
In above table,we took the total numbers of electrons per second and multiply it to Energy deposited by one electron,get total energy deposited per second (which is power).
3.Calculating equilibrium temperature using Stefan–Boltzmann law
If we assume that there is no energy conduction and total energy is just radiated from two surfaces of the radiators which are as big as beam spot,in our case beam spot is 2mm in diameter. According to Stefan–Boltzmann law, this total power radiated will be
= 2Aσ
Where T is radiating temperature P is the radiating power, A is surface area that beam incident and σ is Stefan–Boltzmann constant or Stefan's constant. To reach equilibrium temperature, Power deposited in and power radiated should be. So
so
T =[/(2Aσ)]^{1/4}
Table of equilibrium temperatures
For 2mm diameter spot size and 0.001 time Radiation Length thickness
| Elements | d (m) | 2A( ) | Stefan-Boltzmann Constant | (K) |
| W | 0.002 | 0.00000628 | 329.8 |
4. Results for different Thicknesses and Spot sizes
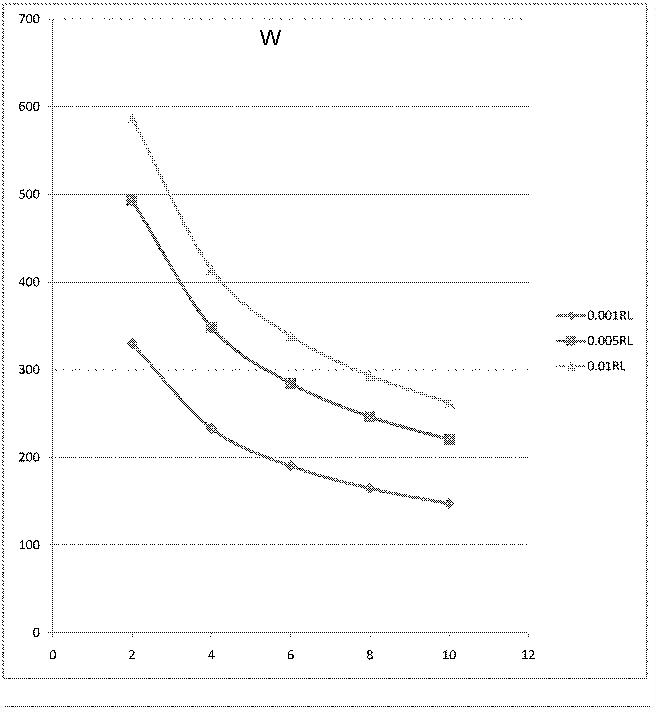
We can calculate separately for Al, W and Ti for different thickness and different beam spot diameter. Following tables are temperature calculation for Al, W Ti and Fe in thickness of 0.001, 0.005 and 0.01 times of Radiation Length, in beam spot of diameter of 2, 4, 6, 8, 10 mm.
W
Equilibrium temperature for W, unit is K. (Melting point of W is 3695K)
| 2(mm) | 4(mm) | 6(mm) | 8(mm) | 10(mm) | |
| 0.001Rl | 239.8 K | 233.2 K | 190.4 K | 164.9 K | 147.5 K |
| 0.005Rl | 493.2 K | 348.7 K | 248.7 K | 246.6 K | 220.6 K |
| 0.01Rl | 586.5 K | 414.7 K | 338.6 K | 293.3 K | 262.3 K |
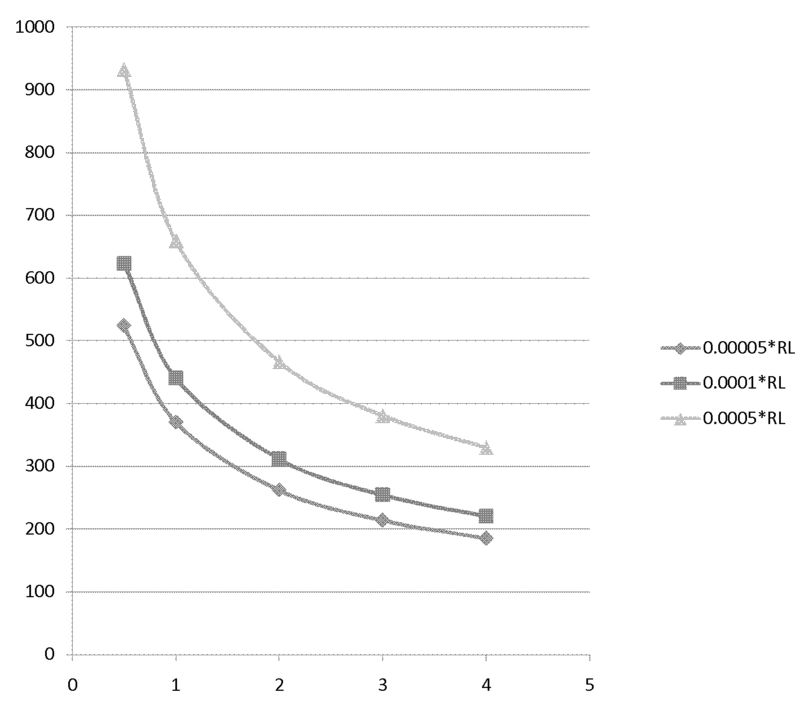
5. Results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width )
Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of 0.00001, 0.0005 and 0.0001 times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm.
W
Equilibrium temperature for W, unit is K. (Melting point of Al is 3695K)
| 1(mm) | 2(mm) | 3(mm) | 4(mm) | |
| 0.00005Rl | 370 K | 262 K | 214 K | 158 K |
| 0.0001Rl | 441 K | 312 K | 254 K | 220 K |
| 0.0005Rl | 660 K | 446 K | 381 K | 330 K |
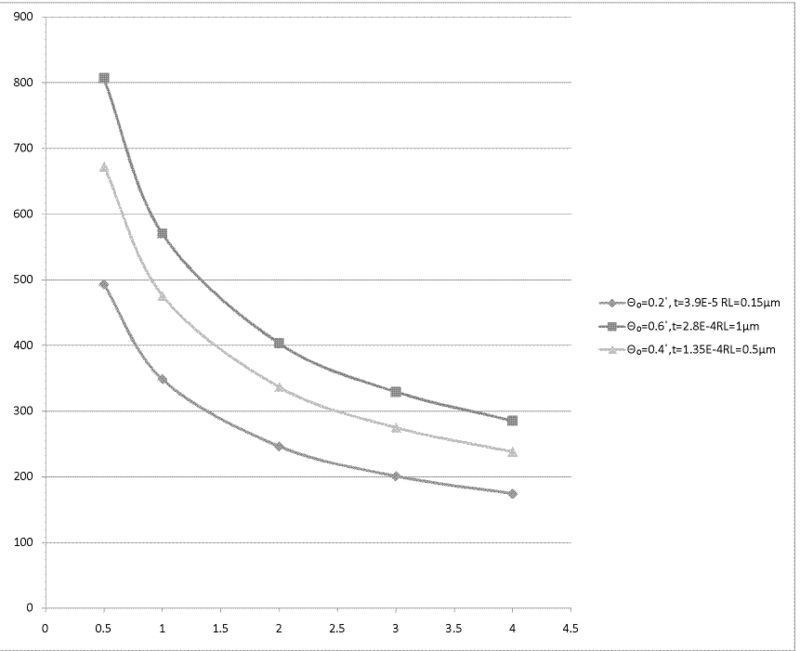
6. More results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width for Θ₀ = 0.2,0.4,0.6 dgrees)
Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of (Θ₀ = ), (Θ₀= ) and (Θ₀ = ) times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm.
W
Equilibrium temperature for W, unit is K. (Melting point of Al is 3695K)
| 2(mm) | 3(mm) | 4(mm) | |
| Θ₀=0.2˚, t=3.9E-5 RL=0.15μm | 246 K | 201 K | 174 K |
| Θ₀=0.4˚,t=1.35E-4RL=0.5μm | 336 K | 275 K | 237 K |
| Θ₀=0.6˚,t=2.8E-4RL=1μm | 404 K | 329 K | 285 K |
PositronsGo Back