Difference between revisions of "Counts Rate (44 MeV LINAC)"
| (299 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | [https://wiki.iac.isu.edu/index.php/Roman_calculation Go Back] |
| − | + | =LINAC parameters used in calculations= | |
| − | + | 1) pulse width 50 ps <br> | |
| − | |||
| − | 1) pulse width 50 | ||
2) pulse current 50 A <br> | 2) pulse current 50 A <br> | ||
3) repetition rate 300 Hz <br> | 3) repetition rate 300 Hz <br> | ||
4) energy 44 MeV <br><br> | 4) energy 44 MeV <br><br> | ||
| + | |||
| + | |||
| + | =Counts Rate for U238 (1/2 mil of Ti radiadot)= | ||
==Number of electrons/sec on radiator== | ==Number of electrons/sec on radiator== | ||
| Line 14: | Line 15: | ||
| − | ==Number of photons/sec | + | ==Number of photons/sec on target== |
===bremsstrahlung=== | ===bremsstrahlung=== | ||
| Line 26: | Line 27: | ||
===radiation length=== | ===radiation length=== | ||
| − | r.l.(Ti) = 3.59 cm | + | r.l.(Ti) = 3.59 cm |
| − | radiator thickness = 12.5 <math>\mu m</math> | + | radiator thickness = 12.5 <math>\mu m</math> |
| − | <math>12.5\mu m | + | <math>\frac{12.5\ \mu m}{3.59\ cm} = 3.48 \cdot 10^{-4} \ r.l.</math><br> |
===steps together...=== | ===steps together...=== | ||
| − | <math>0.1\ \frac{\gamma 's}{(e^- \cdot MeV \cdot r.l.)} \times 3.48 \cdot 10^{-4} r.l. \times 10\ MeV \times 0.47 \cdot 10^{13} \frac{e^-}{sec}=1.64 \cdot 10^{9} \frac{\gamma}{sec}</math><br><br> | + | <math>0.1\ \frac{\gamma 's}{(e^- \cdot MeV \cdot r.l.)} \times 3.48 \cdot 10^{-4} r.l. \times 10\ MeV \times 0.47 \cdot 10^{13} \frac{e^-}{sec}=1.64 \cdot 10^{9} \frac{\gamma}{sec}</math><br><br> |
| − | + | ==Alex factor (GEANT4 calculation)== | |
| − | == | ||
Collimation factor is | Collimation factor is | ||
| − | ''' | + | '''6.85 % of total # of photons''' |
then, incident flux on target is | then, incident flux on target is | ||
| − | <math>1.64 \cdot 10^{9} \frac{\gamma}{sec} \cdot | + | <math>1.64 \cdot 10^{9} \frac{\gamma}{sec} \cdot 6.85\ % = 1.12 \cdot 10^{8} \frac{\gamma}{sec}</math><br><br> |
| + | ==Number of neutrons/sec== | ||
| − | == | + | ===photonuclear cross section for <math>^{238}U(\gamma , F)</math> reaction=== |
| − | + | J. T. Caldwell ''et all.,'' Phys. Rev. '''C21''', 1215 (1980): | |
| − | |||
| − | |||
[[File:phofission_sigma_U238.png]] | [[File:phofission_sigma_U238.png]] | ||
| Line 61: | Line 60: | ||
===target thickness, <math>^{238}U</math>=== | ===target thickness, <math>^{238}U</math>=== | ||
| − | <math>\frac{19.1\ g/cm^3}{238.02\ g/mol} = | + | <math>\frac{19.1\ g/cm^3}{238.02\ g/mol} = 0.08\ \frac{mol}{cm^3} \times \frac{6.02\cdot 10^{23}\ atoms}{mol} = 0.48\cdot 10^{23}\ \frac{atoms}{cm^3}</math> |
| − | + | Let's target thickness = 1 mm: | |
| − | <math>0.48\cdot 10^{23}\ \frac{atoms}{cm^3} \times 1\ cm = 0.48\cdot 10^{ | + | <math>0.48\cdot 10^{23}\ \frac{atoms}{cm^3} \times 0.1\ cm = 0.48\cdot 10^{22}\ \frac{atoms}{cm^2}</math> |
===neutrons per fission=== | ===neutrons per fission=== | ||
| Line 73: | Line 72: | ||
===steps together...yeild=== | ===steps together...yeild=== | ||
| − | <math> Y = \frac{\gamma}{sec} \times t \times \sigma \times 2.4 = </math | + | <math> Y = \frac{\gamma}{sec} \times t \times \sigma \times 2.4 = </math> |
| − | <math> = | + | <math> = 1.12 \cdot 10^{8} \frac{\gamma}{sec} \times 130\ mb \times 0.48\cdot 10^{22}\ \frac{atoms}{cm^2} \times 2.4 = 1.68 \cdot 10^{5}\ \frac{neutrons}{sec}</math><br><br> |
==Worst Case Isotropic Neutrons== | ==Worst Case Isotropic Neutrons== | ||
| − | + | ===checking detector distance=== | |
| + | |||
| + | we want: | ||
| + | |||
| + | the time of flight of neutron >> the pulse width | ||
| + | |||
| + | take the worst case 10 MeV neutron: | ||
| + | |||
| + | <math> E_{tot} = E_{kin} + E_{rest} = 10\ MeV + 938\ MeV = 948\ MeV </math> | ||
| + | |||
| + | <math> \gamma = \frac{E_{tot}}{m_p} = \frac{948\ MeV}{938\ MeV} = 1.0107 </math> | ||
| + | |||
| + | <math> \gamma^2 = \frac{1}{1 - \beta^2} \ \ \ \rightarrow \ \ \ \beta = 0.145\ c</math> | ||
| + | |||
| + | take the neutron detector 1 meter away: | ||
| + | |||
| + | <math> t = \frac{1\ m}{0.145\ c} = \frac{1\ m}{0.145\cdot 3\cdot 10^8\ m/sec} = 23\ ns </math> | ||
| + | |||
| + | 23 ns >> 50 ps <= time resolution is good | ||
| + | |||
| + | ===geometrical factor=== | ||
| + | |||
| + | taking real detector 3" x 2" => S is about 40 cm^2 | ||
| + | |||
| + | 1 meter away | ||
| + | |||
| + | fractional solid angle = <math>\frac{40\ cm^{2}}{4 \pi\ (100\ cm)^{2}} = 3.2 \cdot 10^{-4}</math> <= geometrical acceptance | ||
| + | |||
| + | ==Yield (1/2 mil of Ti and without detector efficiency)== | ||
| + | |||
| + | the yield per second: | ||
| + | |||
| + | <math>1.68 \cdot 10^{5}\ \frac{neutrons}{sec} \times 3.2 \cdot 10^{-4} = 53.8\ \frac{neutrons}{sec} </math><br> | ||
| + | |||
| + | the yield per pulse: | ||
| + | |||
| + | <math> 53.8\ \frac{neutrons}{sec} \times \frac{1\ sec}{300\ pulses} = 0.18\ \frac{neutrons}{pulse} </math> <br><br> | ||
| + | |||
| + | :'''53.8 neutrons/sec <= this experiment is do able''' | ||
| + | |||
| + | :'''0.18 neutrons/pulse <= good for stopping pulse''' | ||
| + | |||
| + | =Counts Rate for U238 (1/2 mil of Al converter)= | ||
| + | |||
| + | ==radiation length== | ||
| + | |||
| + | r.l.(Al) = 8.89 cm | ||
| + | |||
| + | radiator thickness = 12.5 <math>\mu m</math> | ||
| + | |||
| + | <math>\frac{12.5\ \mu m}{8.89\ cm} = 1.41 \cdot 10^{-4} \ r.l.</math><br> | ||
| − | + | ==Calibration factor== | |
| − | + | The only difference from calculations above is: | |
| − | + | 1) radiation length: | |
| − | + | 1.41 (1/2 mil Al) / 3.48 (1/2 mil Ti) = 0.40 | |
| − | + | ==Yield (1/2 mil of Al and without detector efficiency)== | |
| − | ''' | + | :'''53.8 neutrons/sec * 0.40 = 21.5 neutrons/sec ''' |
| − | = | + | :'''0.18 neutrons/pulse * 0.40 = 0.07 neutrons/pulse ''' |
| − | = | + | =Counts Rate for Deuteron (1/2 mil of Ti converter)= |
| − | + | ===photonuclear cross section for <math> ^2H(\gamma , n) </math> reaction=== | |
| + | |||
| + | A. De Graeva ''et all.,'' Phys. Rev. '''C45''', 860 (1992): | ||
[[File:photonuc_sigma_deuteron.png]] | [[File:photonuc_sigma_deuteron.png]] | ||
| Line 104: | Line 155: | ||
in (10,20) MeV region the average cross section, say, is: | in (10,20) MeV region the average cross section, say, is: | ||
| − | '''1000 mb''' | + | '''1000 μb''' |
| + | |||
| + | ===target thickness, <math> D_2O </math>=== | ||
| + | |||
| + | take <math>D_2O</math>, liquid (20°C): | ||
| + | |||
| + | <math> \frac{1.1056\ g/mL}{20.04\ g/mol} = 0.055\ \frac{mol}{cm^3} \times \frac{6.02\cdot 10^{23}\ molecules}{mol} = 0.33\cdot 10^{23}\ \frac{molecules}{cm^3} </math> | ||
| + | |||
| + | <math> 0.33\cdot 10^{23}\ \frac{molecules}{cm^3} \times \frac{2\ deuterons}{molecule} = 0.66\cdot 10^{23}\ \frac{deuterons}{cm^3} </math> | ||
| + | |||
| + | Let's target thickness = 10 cm: | ||
| + | |||
| + | <math>0.66\cdot 10^{23}\ \frac{atoms}{cm^3} \times 10\ cm = 66\cdot 10^{22}\ \frac{atoms}{cm^2}</math> | ||
| + | |||
| + | |||
| + | ===angular distribution of neutron=== | ||
| + | |||
| + | ====P. Rossi ''et all.,'' Phys. Rev. '''C40''', 2412 (1989):==== | ||
| + | |||
| + | [[File:sigma_deuteron_20_40MeV.png|600 px]] | ||
| + | |||
| + | [[File:sigma_deuteron_total.png|300 px]] | ||
| + | |||
| + | |||
| + | ====relativistic kinematics==== | ||
| + | |||
| + | An Introduction to Nuclear and Subnuclear Physics. Emilio Segre (1964) | ||
| + | |||
| + | <math> \tan(\Theta_i) = \frac{1}{\overline{\gamma}} \frac{\sin\Theta_i^*}{\overline{\beta} (E_i^*/p_i^*) + \cos\Theta_i^*}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | asterisks are quantities referred to CM<br> | ||
| + | barred quantities refer to the velocity of the CM | ||
| + | |||
| + | |||
| + | <math> E^* = \left[(m_1+m_2)^2 + 2T_1m_2\right]^{1/2}</math><br> | ||
| + | <math> \overline{\gamma} = \frac{E}{E^*} = \frac{m_1 + m_2 + T_1}{E^*}</math><br> | ||
| + | <math> \overline{\beta} = \frac{p}{E} = \frac{p_1}{m_1 + m_2 + T_1}</math> | ||
| + | |||
| + | |||
| + | <math> E_3^* = \frac{E^{*2} + m_3^2 - m_4^2}{2E*}</math><br> | ||
| + | <math> E_4^* = \frac{E^{*2} + m_4^2 - m_3^2}{2E*}</math><br> | ||
| + | <math> |p_3^*| = |p_4^*| = \left( E_3^{*2} - m_3^2 \right)^{1/2} = \left( E_4^{*2} - m_4^2 \right)^{1/2}</math> | ||
| + | |||
| + | ====calculations==== | ||
| + | |||
| + | {| border="1" cellpadding="20" cellspacing="0" | ||
| + | |- | ||
| + | |<math>T_{\gamma}</math> | ||
| + | ||<math>\Theta_{LAB}</math> | ||
| + | ||<math>\Theta_{CM}</math> | ||
| + | ||<math>\sigma_{T}</math> | ||
| + | ||<math>d \sigma / d \Omega\left(\Theta_{CM}\right)</math> | ||
| + | ||<math>\Omega_{Det}=\frac{A}{r^2}</math> | ||
| + | ||<math>\frac{d \sigma / d \Omega \times \Omega_{Det}}{\sigma_{T}}</math> | ||
| + | |- | ||
| + | |20 MeV || <math>90^o</math> || <math>94.38^o</math> || <math>600\ \mu b</math> | ||
| + | || <math>63\ \mu b/sr</math> || <math>40\cdot 10^{-4}\ sr</math> || <math>4.2\cdot 10^{-4}</math> | ||
| + | |- | ||
| + | |40 MeV || <math>90^o</math> || <math>96.06^o</math> || <math>350\ \mu b</math> | ||
| + | || <math>23\ \mu b/sr</math> || <math>40\cdot 10^{-4}\ sr</math> || <math>2.6\cdot 10^{-4}</math> | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | ====geometrical factor==== | ||
| + | |||
| + | taking average for 20 and 40 MeV photons | ||
| + | |||
| + | geometrical acceptance = <math>\frac{(4.2\cdot 10^{-4} + 2.6\cdot 10^{-4})}{2} = 3.4\cdot 10^{-4}</math> | ||
| + | |||
| + | ===Calibration factor=== | ||
| + | |||
| + | The only differences from calculations above are: | ||
| + | |||
| + | 1) cross section correction: | ||
| + | |||
| + | 1000 μb (D) / 130 mb (238U) = 1/130 | ||
| + | |||
| + | 2) target thickness correction: | ||
| + | |||
| + | <math> \frac{66\cdot 10^{22}\ atoms/cm^2\ (D)}{0.48\cdot 10^{23}\ atoms/cm^2\ (^{238}U)} = 66/0.48 </math> | ||
| + | |||
| + | 3) neutrons per reaction correction: | ||
| + | |||
| + | 1 neutron (D) / 2.4 neutrons(238U) = 1/2.4 | ||
| + | |||
| + | 4) geometrical factor correction: | ||
| + | |||
| + | <math> \frac{3.4\cdot 10^{-4}\ (D)}{3.2\cdot 10^{-4}\ (^{238}U)} = 1.06 </math> | ||
| + | |||
| + | '''total calibration factor is:''' | ||
| + | |||
| + | <math>\frac{1}{130} \times \frac{66}{0.48} \times \frac{1}{2.4} \times \frac{3.4}{3.2} = 0.468</math> | ||
| + | |||
| + | ===Yield (1/2 mil of Ti and without detector efficiency)=== | ||
| + | |||
| + | saying all other factors is the same => | ||
| + | |||
| + | the yield per second : | ||
| + | |||
| + | <math> 53.8\ \frac{neutrons}{sec} \times 0.468 = 25.2\ \frac{neutrons}{sec} </math><br> | ||
| + | |||
| + | the yield per pulse: | ||
| + | |||
| + | <math> 25.2\ \frac{neutrons}{sec} \times \frac{1\ sec}{300\ pulses} = 0.08\ \frac{neutrons}{pulse} </math><br><br> | ||
| − | = | + | =Summary (counts rate without neutron efficiency for different radiator thickness= |
| − | + | {| border="1" cellpadding="20" cellspacing="0" | |
| − | + | ||'''converter''' | |
| + | ||'''target''' | ||
| + | ||'''neutrons/sec''' | ||
| + | ||'''neutrons/pulse''' | ||
| + | |- | ||
| + | ||1/2 mil Ti||<math>^{238}U</math>||53.8||0.18 | ||
| + | |- | ||
| + | ||1/2 mil Al||<math>^{238}U</math>||21.5||0.07 | ||
| + | |- | ||
| + | ||1/2 mil Ti||<math>D_2O</math> ||25.2||0.08 | ||
| + | |- | ||
| + | ||1/2 mil Al||<math>D_2O</math> ||10.1||0.03 | ||
| − | + | |} | |
| − | |||
| − | |||
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||
Latest revision as of 19:03, 24 May 2012
LINAC parameters used in calculations
1) pulse width 50 ps
2) pulse current 50 A
3) repetition rate 300 Hz
4) energy 44 MeV
Counts Rate for U238 (1/2 mil of Ti radiadot)
Number of electrons/sec on radiator
Number of photons/sec on target
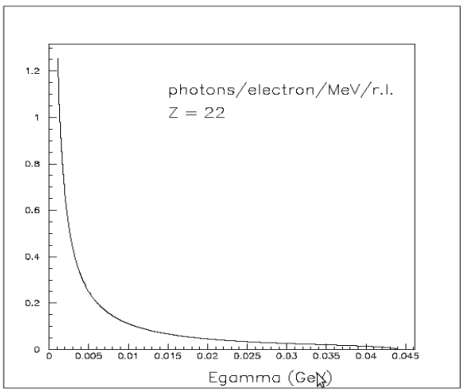
bremsstrahlung
in (10,20) MeV region we have about
0.1 photons/electrons/MeV/r.l
radiation length
r.l.(Ti) = 3.59 cm
radiator thickness = 12.5
steps together...
Alex factor (GEANT4 calculation)
Collimation factor is
6.85 % of total # of photons
then, incident flux on target is
Number of neutrons/sec
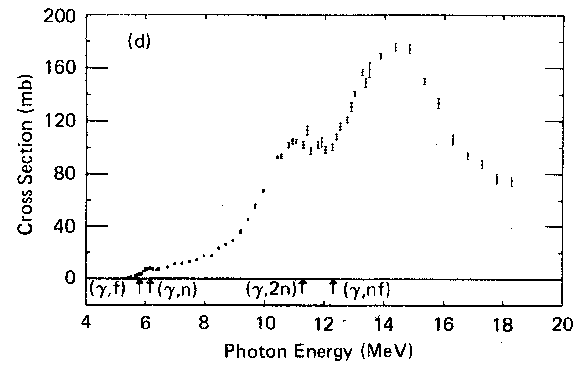
photonuclear cross section for reaction
J. T. Caldwell et all., Phys. Rev. C21, 1215 (1980):
in (10,20) MeV region the average cross section, say, is:
130 mb
target thickness,
Let's target thickness = 1 mm:
neutrons per fission
2.4 neutrons/fission
steps together...yeild
Worst Case Isotropic Neutrons
checking detector distance
we want:
the time of flight of neutron >> the pulse width
take the worst case 10 MeV neutron:
take the neutron detector 1 meter away:
23 ns >> 50 ps <= time resolution is good
geometrical factor
taking real detector 3" x 2" => S is about 40 cm^2
1 meter away
fractional solid angle = <= geometrical acceptance
Yield (1/2 mil of Ti and without detector efficiency)
the yield per second:
the yield per pulse:
- 53.8 neutrons/sec <= this experiment is do able
- 0.18 neutrons/pulse <= good for stopping pulse
Counts Rate for U238 (1/2 mil of Al converter)
radiation length
r.l.(Al) = 8.89 cm
radiator thickness = 12.5
Calibration factor
The only difference from calculations above is:
1) radiation length:
1.41 (1/2 mil Al) / 3.48 (1/2 mil Ti) = 0.40
Yield (1/2 mil of Al and without detector efficiency)
- 53.8 neutrons/sec * 0.40 = 21.5 neutrons/sec
- 0.18 neutrons/pulse * 0.40 = 0.07 neutrons/pulse
Counts Rate for Deuteron (1/2 mil of Ti converter)
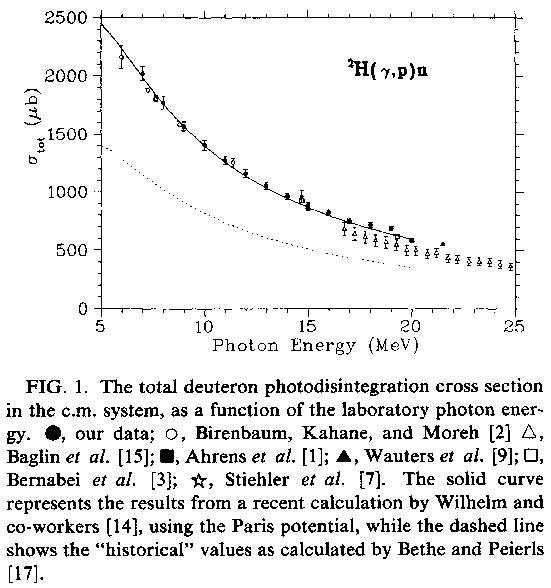
photonuclear cross section for reaction
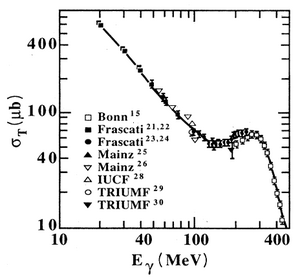
A. De Graeva et all., Phys. Rev. C45, 860 (1992):
in (10,20) MeV region the average cross section, say, is:
1000 μb
target thickness,
take , liquid (20°C):
Let's target thickness = 10 cm:
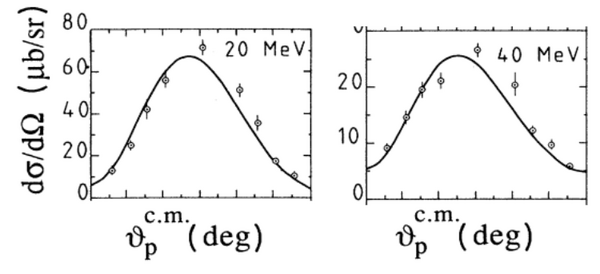
angular distribution of neutron
P. Rossi et all., Phys. Rev. C40, 2412 (1989):
relativistic kinematics
An Introduction to Nuclear and Subnuclear Physics. Emilio Segre (1964)
where
asterisks are quantities referred to CM
barred quantities refer to the velocity of the CM
calculations
| 20 MeV | ||||||
| 40 MeV |
geometrical factor
taking average for 20 and 40 MeV photons
geometrical acceptance =
Calibration factor
The only differences from calculations above are:
1) cross section correction:
1000 μb (D) / 130 mb (238U) = 1/130
2) target thickness correction:
3) neutrons per reaction correction:
1 neutron (D) / 2.4 neutrons(238U) = 1/2.4
4) geometrical factor correction:
total calibration factor is:
Yield (1/2 mil of Ti and without detector efficiency)
saying all other factors is the same =>
the yield per second :
the yield per pulse:
Summary (counts rate without neutron efficiency for different radiator thickness
| converter | target | neutrons/sec | neutrons/pulse |
| 1/2 mil Ti | 53.8 | 0.18 | |
| 1/2 mil Al | 21.5 | 0.07 | |
| 1/2 mil Ti | 25.2 | 0.08 | |
| 1/2 mil Al | 10.1 | 0.03 |