Difference between revisions of "Geometry (44 MeV LINAC exit port)"
Jump to navigation
Jump to search
| (77 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||
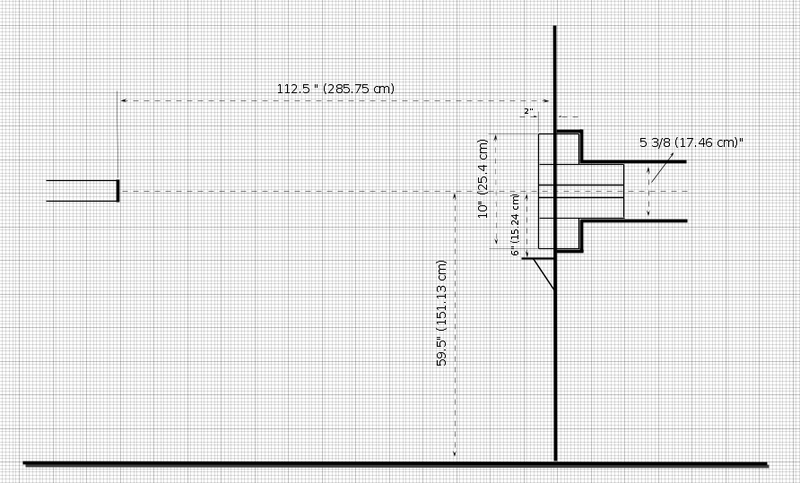
| − | = | + | =90<math>^o</math> exit port measurements= |
| − | [[File:exit_port1.png]]<br><br> | + | [[File:exit_port1.png|800px]]<br><br> |
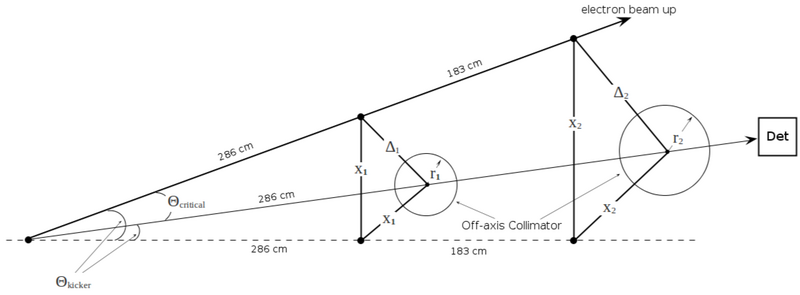
| + | =Critical and Kicker angles= | ||
| − | + | [[File:Beam_up_down.png|800px]]<br> | |
| − | <math>\ | + | <math>\Theta_C = \frac{m_ec^2}{E}</math> |
| + | <math>\Theta_K = tan^{-1}\left(\frac{x_1}{286}\right) | ||
| + | = tan^{-1}\left(\frac{1}{\sqrt{2}}\ \frac{\Delta_1}{286}\right) | ||
| + | = tan^{-1}\left(\frac{1}{\sqrt{2}}\ tan(\Theta_C)\right)</math><br> | ||
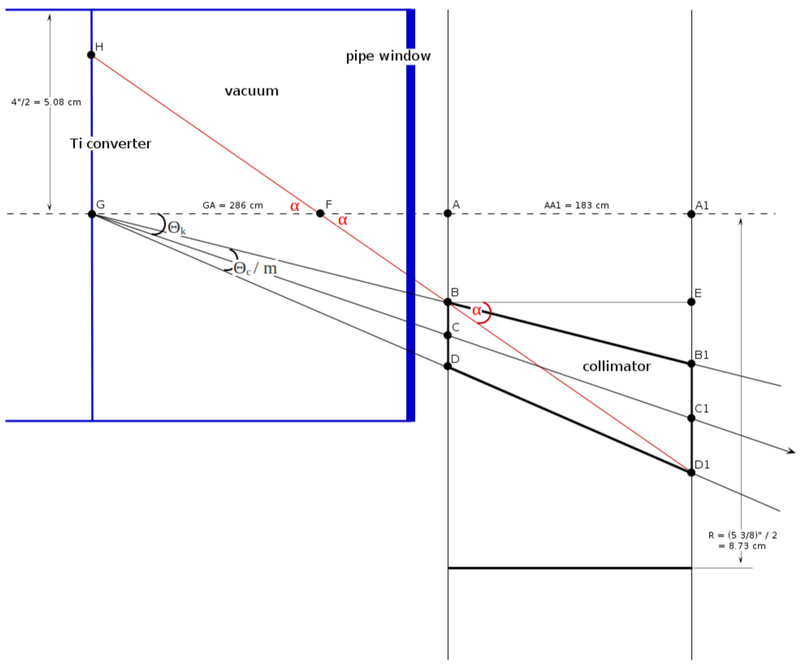
| − | = | + | =General collimator setup= |
| − | + | [[File:minimum_energy_condition.png|800px]] | |
| − | == | + | <math>AC = 286\cdot\tan(\Theta_K)\ cm</math><br> |
| + | <math>A_1C_1 = (286 +183)\cdot\tan(\Theta_K)\ cm</math> | ||
| − | + | <math>BD = 286\cdot\tan(\Theta_C/m)\ cm</math><br> | |
| + | <math>B_1D_1 = (286 + 183)\cdot\tan(\Theta_C/m)\ cm</math><br> | ||
| − | + | <math>\alpha = \frac{A_1D_1 - AB}{183} = \frac{(A_1C_1 + C_1D_1/2) - (AC - B_1D_1/2)}{183}</math> | |
| − | + | <math>FA = AB/\tan(\alpha)\ cm</math><br> | |
| + | <math>GH = (286 - FA)\cdot\tan(\alpha)\ cm</math> | ||
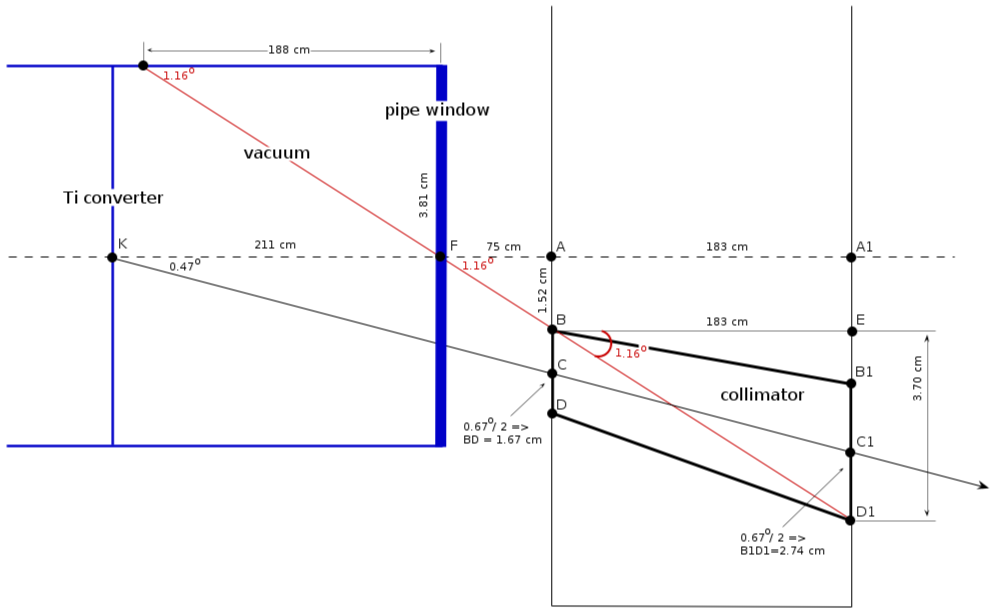
| − | = | + | =Funny pictures...= |
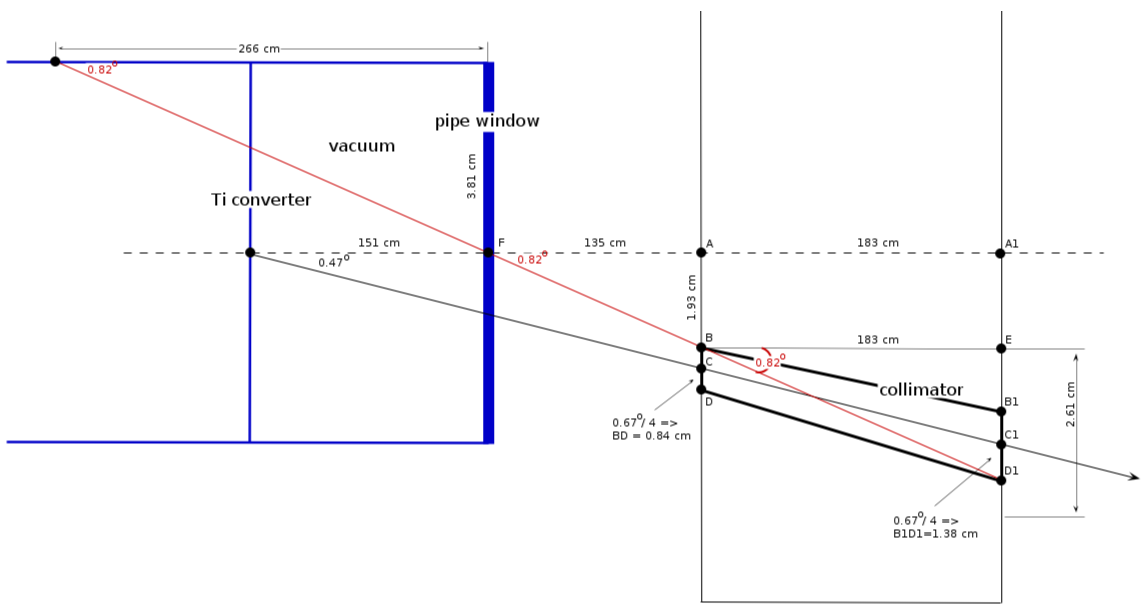
| − | + | ==how it looks (<math> \Theta_c/2</math>, pipe 3")== | |
| − | + | [[File:vacuum_pipe_collimator_0.335_2.png]]<br> | |
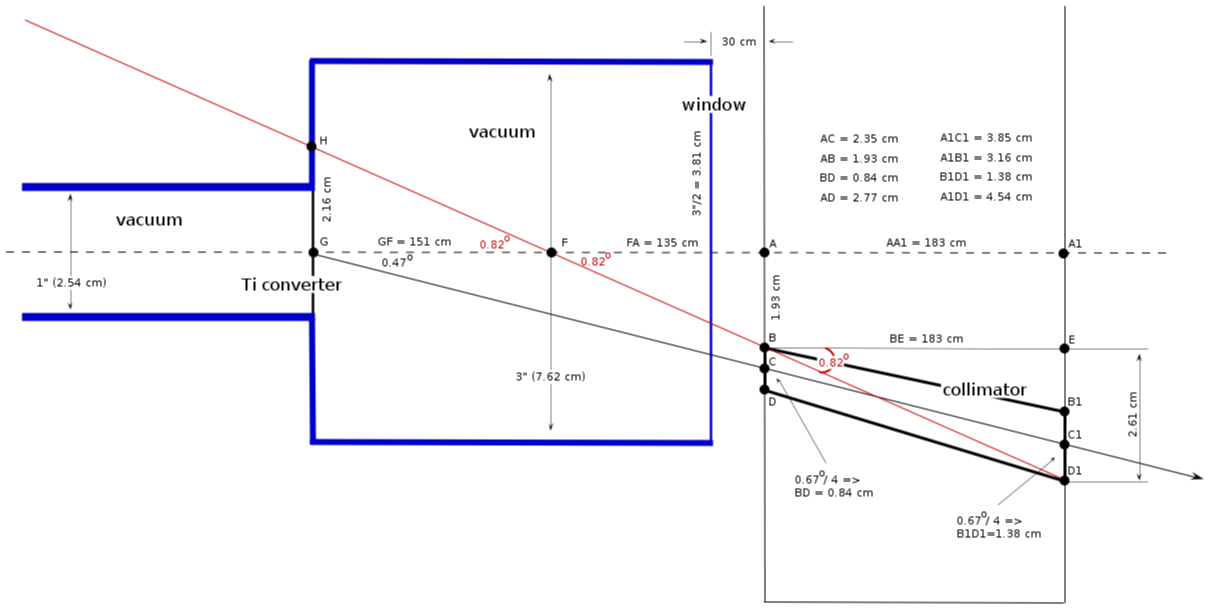
| − | = | + | ==how it looks 1 (<math> \Theta_c/4</math>, pipe 3")== |
| − | [[File: | + | [[File:vacuum_pipe_collimator_0.168_2.png]]<br> |
| − | = | + | ==how it looks 2 (<math> \Theta_c/4</math>, pipe 3")== |
| − | + | [[File:vacuum_pipe_collimator_168_1.png]]<br> | |
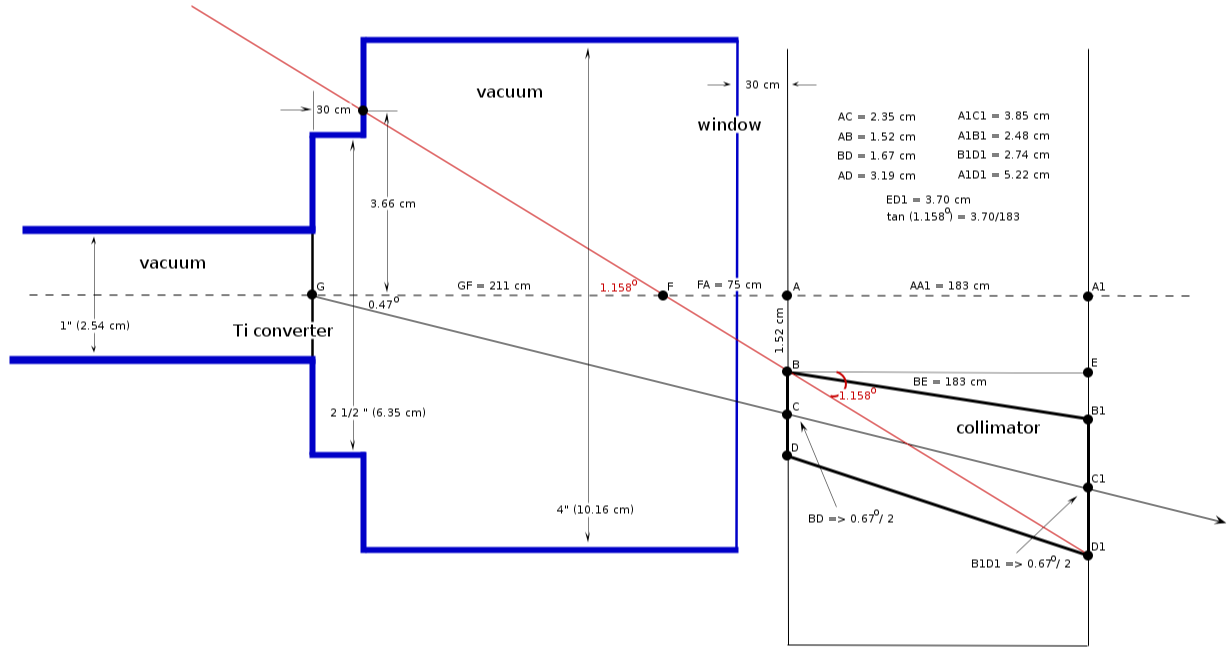
| − | 1) | + | ==how it looks 4 (<math> \Theta_c/2</math>, pipe (2 1/2)" and then pipe 4")== |
| − | + | need to adjust to converter position | |
| − | |||
| − | + | [[File:vacuum_pipe_collimator_335_4.png]]<br> | |
| − | |||
| − | |||
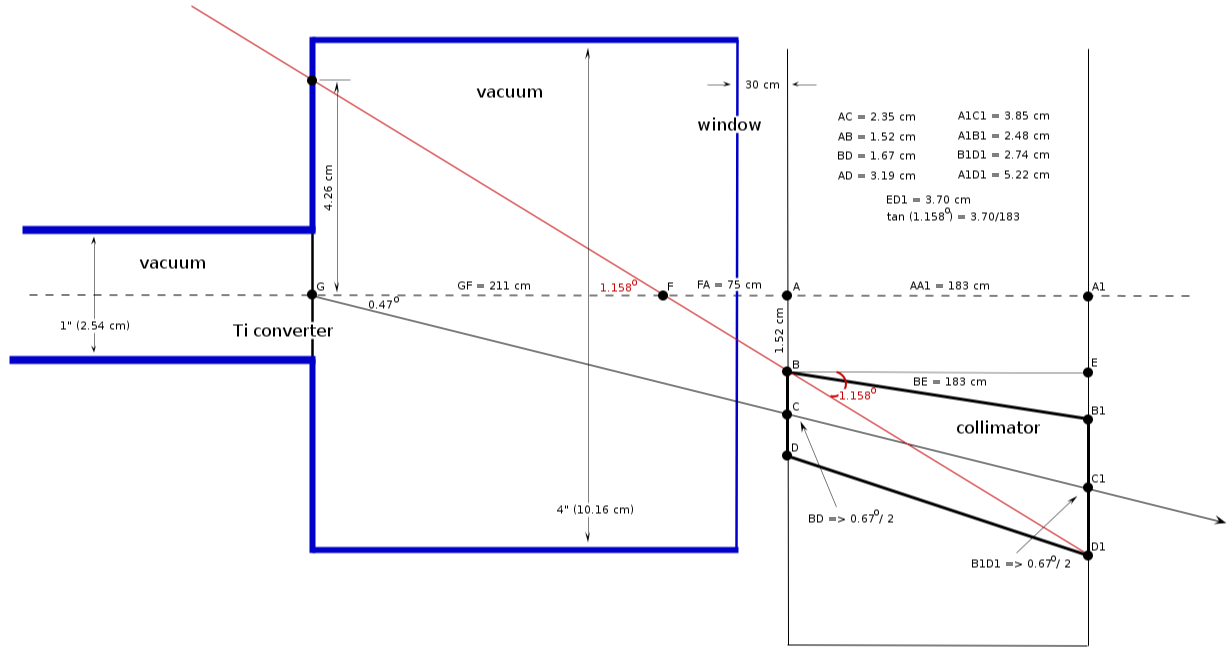
| − | == | + | ==how it looks 5 (<math> \Theta_c/2</math>, box 3"x4" and then pipe 4")== |
| − | + | need to adjust to converter position | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:vacuum_pipe_collimator_335_5.png]]<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[File: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||
Latest revision as of 22:49, 20 June 2010
90 exit port measurements
Critical and Kicker angles
General collimator setup
Funny pictures...
how it looks (, pipe 3")
how it looks 1 (, pipe 3")
how it looks 2 (, pipe 3")
how it looks 4 (, pipe (2 1/2)" and then pipe 4")
need to adjust to converter position
how it looks 5 (, box 3"x4" and then pipe 4")
need to adjust to converter position