Difference between revisions of "Brian Articles"
m (Protected "Brian Articles" ([edit=brian] (indefinite) [move=brian] (indefinite) [read=brian] (indefinite))) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 4: | Line 4: | ||
===Theory=== | ===Theory=== | ||
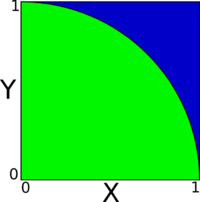
Consider the area of a circle. From elementary school, the equation for the area of a circle is <math>A = \pi r^2</math> where A is the area and r is the radius. If we know the radius and the area of a circle, then we can find the value of <math>\pi</math>. We set the problem up as according to the following diagram: | Consider the area of a circle. From elementary school, the equation for the area of a circle is <math>A = \pi r^2</math> where A is the area and r is the radius. If we know the radius and the area of a circle, then we can find the value of <math>\pi</math>. We set the problem up as according to the following diagram: | ||
| − | [[File:pi_quadrant]] | + | [[File:pi_quadrant.png|200px|none]] |
| − | The green area is one quarter of a circle with radius of 1 | + | The green area is one quarter of a circle with radius of 1, while the blue is a square with a side length of 1. The area of the square is <math>A_{\text{sq}} = 1^2 = 1 </math>. |
Likewise the area for the circle section is <math>A_{\text{circ}} = \frac{1}{4} \pi r^2 = \frac{\pi}{4} </math>. | Likewise the area for the circle section is <math>A_{\text{circ}} = \frac{1}{4} \pi r^2 = \frac{\pi}{4} </math>. | ||
Latest revision as of 01:59, 31 December 2010
Monte-Carlo Calculation of Pi
One of my favorite algorithms is the Monte-Carlo calculation of . Although is method is very inefficient, it is also highly parallelizable and easy to understand.
Theory
Consider the area of a circle. From elementary school, the equation for the area of a circle is where A is the area and r is the radius. If we know the radius and the area of a circle, then we can find the value of . We set the problem up as according to the following diagram:
The green area is one quarter of a circle with radius of 1, while the blue is a square with a side length of 1. The area of the square is . Likewise the area for the circle section is .
Using the Pythagorean theorem, the outline of the circle centered at (0,0) is . So if , then a point lies within the circle (green area). Now, choose a point by randomly selecting an x and y between 0.0 and 1.0. If it satisfies the above inequality, then it lies within the circle. All of the points will lie with the square. Using N for the number of "hits" in each section,
Solving for gives
So by using a number of randomly selected points, we can estimate the value of .
Code
This basic code is in C++ and utilizes the posix functions srand48 (seeds the random generator) and drand48 (returns a double between 0.0 and 1.0).
#include <iostream>
#include <stdlib.h> //rand functions
using namespace std;
//these defines allow us to set N at compile time, i.e.
//gcc -DN=200000
#ifndef N
#define N 10000
#endif
int main()
{
srand48(42); //42 should be replaced with time() or whatnot
double x, y;
unsigned int circle = 0;
cout << "Running " << N << " trials" << endl;
for(unsigned int i=0; i<N; i++)
{
x = drand48();
y = drand48();
if(x*x + y*y < 1.0)
circle++; //
}
cout << "Pi is: " << 4.0*(double)circle/(double)N << endl;
return 0;
}
When running the output looks like this:
brian@winnebago:~/code/cpi$ g++ cpi.cpp -DN=100 -o cpi && ./cpi Running 100 trials Pi is: 3.16
brian@winnebago:~/code/cpi$ g++ cpi.cpp -DN=10000 -o cpi && ./cpi Running 10000 trials Pi is: 3.1676
brian@winnebago:~/code/cpi$ g++ cpi.cpp -DN=10000000 -o cpi && ./cpi Running 10000000 trials Pi is: 3.14179
brian@winnebago:~/code/cpi$ g++ cpi.cpp -DN=1000000000 -o cpi && ./cpi Running 1000000000 trials Pi is: 3.14161
With more trials, the calculated value of approaches the real value,
Benchmarking Code
Quick-n-Dirty with time
The easiest way to benchmark the time of a program is simply using the time command:
brian@winnebago:~/code/cpi$ time ./cpi Running 100000000 trials Pi is: 3.14133 real 0m5.845s user 0m5.830s sys 0m0.010s
- "real" is the actual elapsed time the program took to run (often referred to as the wall-clock time).
- "user" is the amount of time that the OS spent running you actual code (this is the one that you usually pay the most attention to).
- "sys" is the amount of time that the OS spent on your behalf doing things in the kernel, like I/O.
This is useful to test in the real-world, including the effects of program initialization, hardware limitations, and network time. However, all of these factors can also add significantly noise of the measurement as they can vary according to system load, network load, systems caches, any many, many other factors. You will want to test a program many times to gain confidence in any numbers returned. As an example, compare these runs of exactly the same command:
brian@winnebago:~/gumstix$ time find ./ | wc -l 275404 real 0m53.946s user 0m0.710s sys 0m2.990s
brian@winnebago:~/gumstix$ time find ./ | wc -l 275404 real 0m1.241s user 0m0.340s sys 0m0.610s brian@winnebago:~/gumstix$ time find ./ | wc -l 275404 real 0m0.891s user 0m0.290s sys 0m0.510s
brian@winnebago:~/gumstix$ time find ./ | wc -l 275404 real 0m0.806s user 0m0.190s sys 0m0.550s
The first search took almost 54s as the filesystem tree wasn't cached in RAM. Subsequent searches of the same file tree are faster as the data is now in RAM and the hard drive no longer needs to be accessed. This admittedly contrived example none-the-less shows how there can be unforeseen side-effects when benchmarking your code.
Loop Unrolling
Motivation
One area of Computer Science interest to me is neural networks, especially feed-forward neural networks. Because of the way that neural networks learn, they need to evaluate a large number of different weight combinations over a large number of samples. Since evaluating the value of each node is just a dot product of a node's weights and the values of the previous layer, the nexus of fast NN evaluation come down to fast dot products. The dot product of x and y is , or the sum of all the product of the ith components.
The classic C code for computing a dot product is:
double dot(double *a, double *b, size_t s)
{
double sum = 0.0;
for(int i=0; i<s; i++)
{
sum += a[i]*b[i];
}
return sum;
}
Assuming that the floating-point operations are done with a math co-processor (ie. on any non-embedded CPU), most of the overhead comes from counting the index and comparing against the end of the loop. In optimizing this looping procedure, how can we reduce the loop counting overhead? How can we write code to give the compiler hints about what operations vector processors (SSE, AltiVec, etc.) can handle more efficiently. How do the optimization arguments given to the compiler affect code performance?