Difference between revisions of "Qweak Qsqrd Tracking"
| (23 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=Tracking system Description= | =Tracking system Description= | ||
| − | The Qweak tracking system is composed of three tracking regions. Region 1 is a GEM based ionization chamber which measures the radial distance of a hit from the beam pipe center and is located | + | The Qweak tracking system is composed of three tracking regions. Region 1 is a GEM based ionization chamber which measures the radial distance of a hit from the beam pipe center and is located 132 cm away from a 35 cm long target. Region 2 is a drift chamber with 6 layers located XXX m from target center. A Torous magnet is place centered 2 meters from the target which selects elasticly scattered electrons that pass through a primary collimator just before the magnet. Region 2 is another drift chamber located just in front of the quartz cherenkov detectors. A scintillator appears after the quartz cherenkov detector which is used to trigger the tracking system. |
| + | |||
| + | |||
| + | The target is located at Z=-660 cm and has a length of 35 cm. R1 is located at Z=-528 cm, or at most 132 cm from the center of the 35 cm long target. | ||
=<math>Q^2</math> for Elastic Scattering= | =<math>Q^2</math> for Elastic Scattering= | ||
| Line 8: | Line 11: | ||
:<math><\delta Q>^2 = \left ( \frac{\partial Q}{\partial E} \right )^2 \left( \delta E \right )^2 + \left ( \frac{\partial Q}{\partial \theta} \right )^2 \left( \delta \theta \right )^2 + \left ( \frac{\partial Q}{\partial \theta \partial E} \right )^2 \left( \delta \theta \delta E \right )</math> | :<math><\delta Q>^2 = \left ( \frac{\partial Q}{\partial E} \right )^2 \left( \delta E \right )^2 + \left ( \frac{\partial Q}{\partial \theta} \right )^2 \left( \delta \theta \right )^2 + \left ( \frac{\partial Q}{\partial \theta \partial E} \right )^2 \left( \delta \theta \delta E \right )</math> | ||
| − | := <math>\frac{16 E_i^2 M_p^2 \sin^2(\theta/2)}{(E_i +M_p - E_i \cos(\theta/2))^6} \times \left [ \left ( 4 M_p^4 \sin^2(\theta/2) + 24 E_i M_p^3 \sin^4(\theta/2) + 52 E_i^2M_p^2 \sin^6(\theta/2) + 48 E_i^3 M_p \sin^8(\theta/2) + 16 E_i^4 \sin^{10}(\theta/2) \right ) | + | := <math>\frac{16 E_i^2 M_p^2 \sin^2(\theta/2)}{(E_i +M_p - E_i \cos(\theta/2))^6} \times \left [ A (\delta E)^2 + B \left ( \delta \theta \right )^2+ C \left ( \delta E \delta \theta\right )^2\right ]</math> |
| − | : | + | :<math></math> |
| + | |||
| + | Where | ||
| + | |||
| + | :<math>A=\left ( 4 M_p^4 \sin^2(\theta/2) + 24 E_i M_p^3 \sin^4(\theta/2) + 52 E_i^2M_p^2 \sin^6(\theta/2) + 48 E_i^3 M_p \sin^8(\theta/2) + 16 E_i^4 \sin^{10}(\theta/2) \right )</math> | ||
| + | :<math>B=\left \{ E_i^2M_p^4 +4 E_i^4 M_p^2 \sin^4(\theta/2)\right \}\cos^2(\theta/2) + E_i^3 M_p^3 \sin^2(\theta/2)</math> | ||
| + | :<math>C=4M_p^2 \cos^2(\theta/2)</math> | ||
== Error using only R1 == | == Error using only R1 == | ||
| Line 17: | Line 26: | ||
;<math>\tan(\theta) = \frac{r \sin(\theta)}{r \cos(\theta)} = \frac{d}{Z} | ;<math>\tan(\theta) = \frac{r \sin(\theta)}{r \cos(\theta)} = \frac{d}{Z} | ||
</math> | </math> | ||
| − | assuming the error is<math> \delta d = 100 \mu m</math> and <math>\delta Z = | + | assuming the error is<math> \delta d = 100 \mu m</math> and <math>\delta Z = 35 cm</math> = length of the target |
| − | ;<math>\frac{\delta \tan(\theta)}{\theta} = \sqrt{\left( \frac{\delta d }{d} \right )^2+ \left( \frac{\delta Z }{Z} \right )^2}</math> | + | ;<math>\frac{\delta \tan(\theta)}{\tan(\theta)} = \sqrt{\left( \frac{\delta d }{d} \right )^2+ \left( \frac{\delta Z }{Z} \right )^2}</math> |
| − | If Z = | + | If Z = 132 cm and d = 15 cm |
then | then | ||
| − | + | :<math>\frac{\delta \tan(\theta)}{\tan \theta}= 0.27 \approx \frac{\delta \theta}{\theta}</math>; dominated by <math>\delta Z</math> error. | |
| + | :<math>\Rightarrow \frac{\delta Q^2}{Q^2} = 54%</math> with Term "B" above being the biggest contributor to the error because <math>\frac{\delta Z}{Z}</math> = 26% | ||
| + | |||
| + | ;Use R2 and R1 together to reduce the <math>\frac{\delta Z}{Z}</math> error. | ||
==Using only R1 and R2== | ==Using only R1 and R2== | ||
| Line 37: | Line 49: | ||
| − | [[ | + | |
| + | ===Qqsrd Error code=== | ||
| + | |||
| + | [[Qweak_Qsqrd_Error_Code_2Trackers]] | ||
| + | |||
| + | = References= | ||
| + | |||
| + | [http://arxiv.org/abs/0908.0851 Track fitting by Kalman Filter method for a prototype cosmic ray muon detector] | ||
Latest revision as of 15:07, 7 August 2009
Tracking system Description
The Qweak tracking system is composed of three tracking regions. Region 1 is a GEM based ionization chamber which measures the radial distance of a hit from the beam pipe center and is located 132 cm away from a 35 cm long target. Region 2 is a drift chamber with 6 layers located XXX m from target center. A Torous magnet is place centered 2 meters from the target which selects elasticly scattered electrons that pass through a primary collimator just before the magnet. Region 2 is another drift chamber located just in front of the quartz cherenkov detectors. A scintillator appears after the quartz cherenkov detector which is used to trigger the tracking system.
The target is located at Z=-660 cm and has a length of 35 cm. R1 is located at Z=-528 cm, or at most 132 cm from the center of the 35 cm long target.
for Elastic Scattering
General Expression for Elastic scattering error
- =
Where
Error using only R1
This simple calculation assumes that only the electron distance from the beamline measured 0.5 m from the target center by the GEM detector will be used to calculate .
assuming the error is and = length of the target
If Z = 132 cm and d = 15 cm
then
- ; dominated by error.
- with Term "B" above being the biggest contributor to the error because = 26%
- Use R2 and R1 together to reduce the error.
Using only R1 and R2
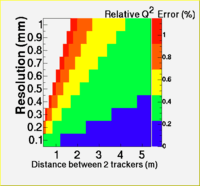
R1 and R2 together may be used to reconstruct straight tracks and determine the of elasticly scattered electrons. The for elastically scattered electrons can be determine if the incident electron energy (E) and the scattered electron zenith angle are known where the "z-axis" of a spherical coordinate system is directed down the beam pipe in the direction of the incident electron. The Region 1 tracking system measures the distance of the scattered electron from the center of the beam pipe . For a point target one would be able to determine the scattering angle \theta using the distance of the Region 1 detector from the target. The Qweak target, however is extended in the "z" direction and prevents an accurate calculation of with just one tracking element. A second tracking element, Region 2, along with knowledge of the "X" and "Y" location of the incident beam will enable a determination of a plane intersecting the z-axis at the interaction point. The scattering angle can be determined using
or
Qqsrd Error code
Qweak_Qsqrd_Error_Code_2Trackers
References
Track fitting by Kalman Filter method for a prototype cosmic ray muon detector