Difference between revisions of "Eγ vs probability with 8 cm of D20"
Jump to navigation
Jump to search
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||
| + | |||
| + | |||
<math>Probability = \sigma \times \rho \times thickness</math> | <math>Probability = \sigma \times \rho \times thickness</math> | ||
| − | <math>\rho | + | <math>\rho(D _20) = 1 \frac{g}{cm^{3}} \times \frac {20}{18} \times \frac{6.022 \cdot 10^{23}}{20g}\times 2 = 6.6242 \cdot 10^{22}</math> |
| Line 22: | Line 25: | ||
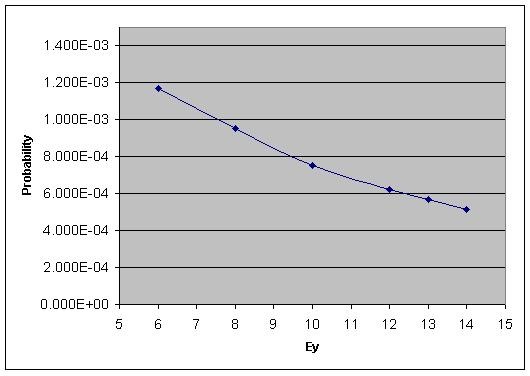
<math>14 MeV = 963 \cdot 10^{-30} \times 6.6242 \cdot 10^{22} \times 8 cm = 5.15 \cdot 10^{-4}</math> | <math>14 MeV = 963 \cdot 10^{-30} \times 6.6242 \cdot 10^{22} \times 8 cm = 5.15 \cdot 10^{-4}</math> | ||
| − | [[Image: | + | [[Image:probability_d20_8_cm_2.jpg]] |
| + | |||
| + | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||