Difference between revisions of "Radiators Temperature"

From New IAC Wiki
Jump to navigation Jump to search
 
(10 intermediate revisions by the same user not shown)
Line 1: Line 1:
 +
[http://wiki.iac.isu.edu/index.php/HRRL Go Back]
 +
 +
 
=Calculating Radiators Equilibrium Temperature=
 
=Calculating Radiators Equilibrium Temperature=
 
==1.Calculating number of particles per second ==
 
==1.Calculating number of particles per second ==
Line 65: Line 68:
 
|-
 
|-
 
|Elements
 
|Elements
−
|<math>(dE/dx)_{coll}</math>
+
|<math>(dE/dx)_{coll} (MeV \; cm^2/g)</math>
 
|t( <math> gcm^{-2}</math>)
 
|t( <math> gcm^{-2}</math>)
 
|<math>E_{dep one}</math> (MeV)
 
|<math>E_{dep one}</math> (MeV)
Line 84: Line 87:
  
 
                                   <math>P{dep}= E{dep/s} = ( E {dep by one})*(Number of electron per second)</math>
 
                                   <math>P{dep}= E{dep/s} = ( E {dep by one})*(Number of electron per second)</math>
 +
 
==3.Calculating equilibrium temperature using Stefan–Boltzmann law==
 
==3.Calculating equilibrium temperature using Stefan–Boltzmann law==
 
If we assume that there is no energy conduction and total energy is just radiated from two surfaces of the radiators which are as big as beam spot,in our case beam spot is 2mm in diameter.  According to Stefan–Boltzmann law, this total power radiated will be  
 
If we assume that there is no energy conduction and total energy is just radiated from two surfaces of the radiators which are as big as beam spot,in our case beam spot is 2mm in diameter.  According to Stefan–Boltzmann law, this total power radiated will be  
Line 322: Line 326:
  
  
−
==6. More results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width ) ==
+
==6. More results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width for Θ₀ = 0.2,0.4,0.6 dgrees) ==
  
−
Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of <math>3.9*10^{-5}</math> (Θ₀ = <math>0.2^{0}</math>), <math>1.35*10^{-4}</math>(Θ₀= <math>0.4^{0}</math>) and <math>2.8*10^{-4}</math>(Θ₀ = <math>0.6^{0}</math>) times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm.
+
Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of <math>3.9*10^{-5}</math> (Θ₀ = <math>0.2^{o}</math>), <math>1.35*10^{-4}</math>(Θ₀= <math>0.4^{o}</math>) and <math>2.8*10^{-4}</math>(Θ₀ = <math>0.6^{o}</math>) times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm.
  
 
===Al===
 
===Al===
Line 362: Line 366:
 
| Θ₀=0.2˚, t=3.9E-5 RL=0.15μm|| 246 K|| 201 K|| 174 K
 
| Θ₀=0.2˚, t=3.9E-5 RL=0.15μm|| 246 K|| 201 K|| 174 K
 
|-  
 
|-  
−
| Θ₀=0.4˚,t=1.35E-4RL=0.5μm  || 336 K|| 276 K|| 237 K
+
| Θ₀=0.4˚,t=1.35E-4RL=0.5μm  || 336 K|| 275 K|| 237 K
 
|-  
 
|-  
 
| Θ₀=0.6˚,t=2.8E-4RL=1μm    || 404 K|| 329 K|| 285 K
 
| Θ₀=0.6˚,t=2.8E-4RL=1μm    || 404 K|| 329 K|| 285 K
Line 407: Line 411:
 
|-
 
|-
 
|-
 
|-
−
| Θ₀=0.2˚, t=3.9E-5 RL=0.7μm|| K|| K|| K
+
| Θ₀=0.2˚, t=3.9E-5 RL=0.7μm|| 310 K|| 253 K|| 219 K
 
|-  
 
|-  
−
| Θ₀=0.4˚,t=1.35E-4RL=2.5μm || K|| K|| K
+
| Θ₀=0.4˚,t=1.35E-4RL=2.5μm || 423 K|| 346 K|| 299 K
 
|-  
 
|-  
−
| Θ₀=0.6˚,t=2.8E-4RL=5μm    || K|| K|| K
+
| Θ₀=0.6˚,t=2.8E-4RL=5μm    || 508 K|| 415 K|| 359 K
 
|-
 
|-
 
|}
 
|}
  
 
[[Image:Fe_3.jpg|down|800px]]
 
[[Image:Fe_3.jpg|down|800px]]
 +
 +
[http://wiki.iac.isu.edu/index.php/HRRL Go Back]

Latest revision as of 06:34, 5 February 2009

Go Back


Calculating Radiators Equilibrium Temperature

1.Calculating number of particles per second

We have electron beam of:

Frequency: f=1000Hz

Peak current: I=10mAmp=0.01 Amp

Pulse width: ∆t= 50 ns=5*10-8 seconds

So, how many electrons we have in each second?

By Q=It, we have 

                                            N*e=f*I*∆t

Where Ne is the total electron numbers hits target per second, e is electron charge and f, I and ∆t are given above. So 

                          N= f*I*∆t/e=1000*0.01*5*10-8/(1.6*10-19)=3.12075*1012

So, we have around 3.12075*1012 electrons hit radiator per second.

2.Calculating Energy deposited per second

If we find the energy deposited by each electron and multiply to the total number of electrons in each second, we will find the total energy per second deposited in radiator.

To find energy deposited by each electron, we need to use formula 

                                                    [math] E_{dep  one}=(dE/dx)_{coll}*t [/math]


Where is [math] E_{dep one}[/math] is energy deposited by one electron, [math](dE/dx)_{coll}[/math] is mean energy loss (also stopping power) by collision of electron and t is thickness of the radiator.

Actually, energy loss of electron comes from two parts: the emission of electromagnetic radiation arising from scattering in the electric field of a nucleus (bremsstrahlung) and collisional energy loss when passing through matter. But bremsstrahlung will not contribute to the temperature, since it is radiation.

Stopping power can be found from nuclear data tables [math] (dE/dx)_{ave} [/math] and thickness is 0.001 times of radiation length. From Particle Data group we got radiation length and average total stopping powers around 15MeV for electrons in these materials from National Institute of Standards and Technology

Table of Radiation Lengths

Note:These data is from Particle Data group,Link: [1].

Elements Radiation Lengths [math] (g/cm^{2} )[/math]
Al 24.01
W 6.76
Ti 16.16
Fe 13.84


Table of energy calculations

For the thickness of 0.001 Radiation Length (0.0001RL) of radiators. Note: [math](dE/dx)_{coll}[/math] is from National Institute of Standards and Technology. Link: [[2]])

Elements [math](dE/dx)_{coll} (MeV \; cm^2/g)[/math] t( [math] gcm^{-2}[/math]) [math]E_{dep one}[/math] (MeV) [math]E_{dep/s}[/math] (MeV/s) [math]E_{dep/s}[/math] (J/s)
Al 1.676 0.02401 0.00402076 [math]1.26*10^{11}[/math] [math]2.01*10^{-2}[/math]
W 1.247 0.00676 0.00842972 [math]2.63*10^{10}[/math] [math]4.21*10^{-3}[/math]
Ti 1.555 0.01616 0.0251288 [math]7.84*10^{10} [/math] [math]1.26*10^{-2}[/math]
Fe 1.529 0.01384 0.02116136 [math]6.60*10^{10}[/math] [math]1.06*10^{-2}[/math]

In above table,we took the total numbers of electrons per second and multiply it to Energy deposited by one electron,get total energy deposited per second (which is power). 

                                  [math]P{dep}= E{dep/s} = ( E {dep by one})*(Number of electron per second)[/math]

3.Calculating equilibrium temperature using Stefan–Boltzmann law

If we assume that there is no energy conduction and total energy is just radiated from two surfaces of the radiators which are as big as beam spot,in our case beam spot is 2mm in diameter. According to Stefan–Boltzmann law, this total power radiated will be 

                                                        [math] P_{rad}[/math]= 2Aσ[math]T^{4}[/math]

Where T is radiating temperature P is the radiating power, A is surface area that beam incident and σ is Stefan–Boltzmann constant or Stefan's constant. To reach equilibrium temperature, Power deposited in and power radiated should be. So 

                                                       [math] P_{dep}=P_{rad} [/math]

so 

                                              T =[[math]  P_{dep}[/math]/(2Aσ)]^{1/4}


Table of equilibrium temperatures

For 2mm diameter spot size and 0.001 time Radiation Length thickness

Elements d (m) 2A( [math] m^{2}[/math]) Stefan-Boltzmann Constant [math]T_{equ}[/math] (K)
Al 0.002 0.00000628 [math]5.6704*10^{-8}[/math] 487.5
W 0.002 0.00000628 [math]5.6704*10^{-8}[/math] 329.8
Ti 0.002 0.00000628 [math]5.6704*10^{-8}[/math] 433.4
Fe 0.002 0.00000628 [math]5.6704*10^{-8}[/math] 415.2

4. Results for different Thicknesses and Spot sizes

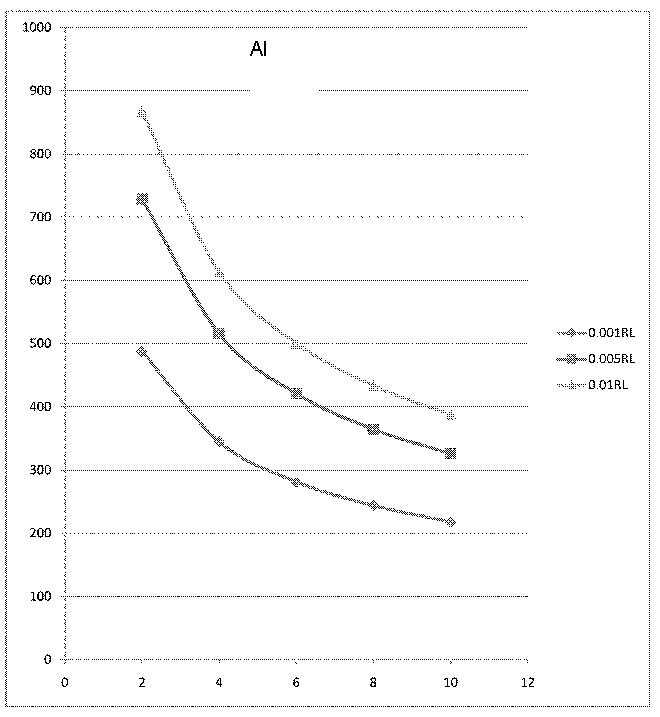
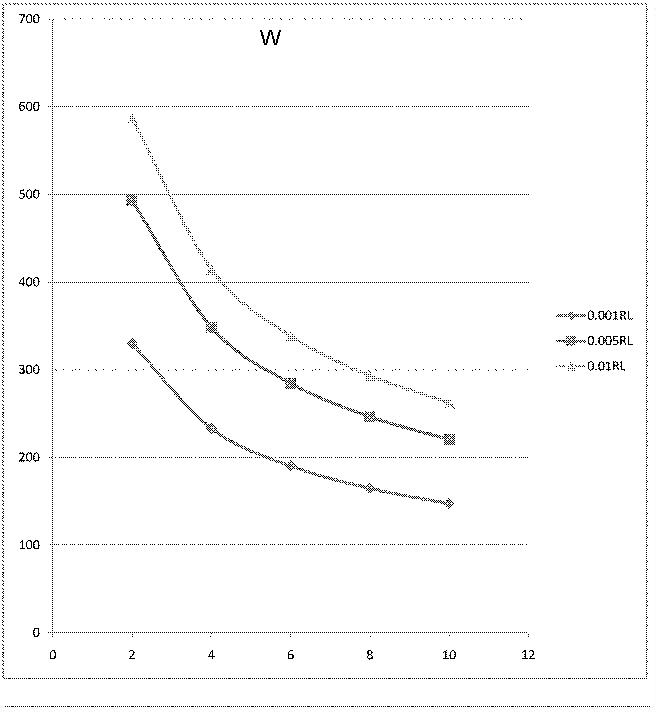
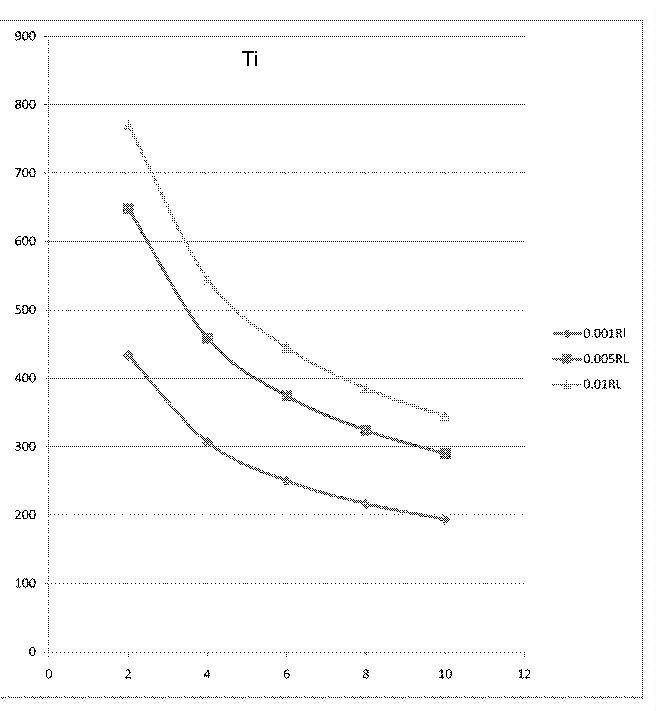
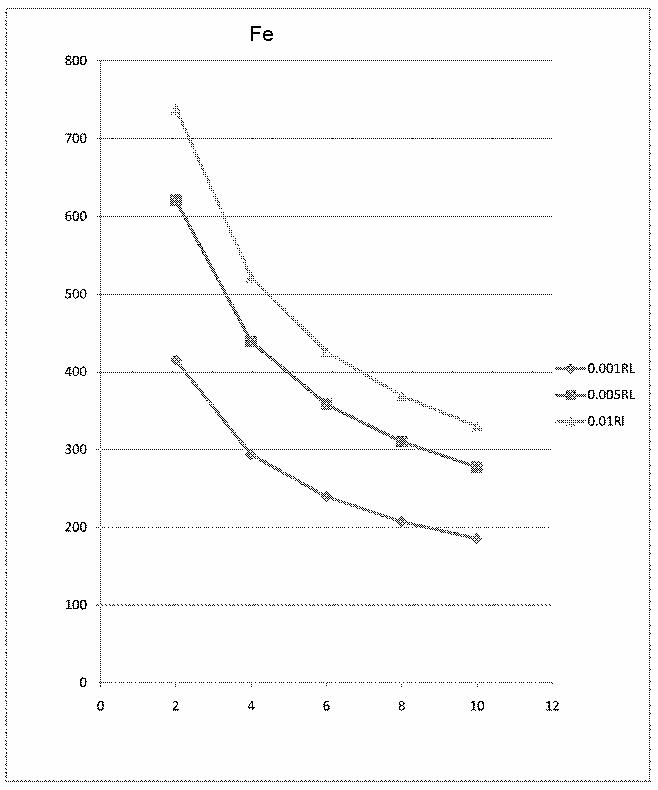
We can calculate separately for Al, W and Ti for different thickness and different beam spot diameter. Following tables are temperature calculation for Al, W Ti and Fe in thickness of 0.001, 0.005 and 0.01 times of Radiation Length, in beam spot of diameter of 2, 4, 6, 8, 10 mm.

Al

Equilibrium temperature for Al, unit is K. (Melting point of Al is 933K)

2(mm) 4(mm) 6(mm) 8(mm) 10(mm)
0.001RlK 487.5 K 344.7 K 281.5 K 234.8 K 218.0 K
0.005Rl K 729.1 K 515.5 K 420.9 K 364.5 K 326.0 K
0.01Rl K 867.0 K 613.1 K 550.6 K 433.5 K 387.7 K

Equilibrium Temperature for Al .jpg

W

Equilibrium temperature for W, unit is K. (Melting point of W is 3695K)

2(mm) 4(mm) 6(mm) 8(mm) 10(mm)
0.001Rl 239.8 K 233.2 K 190.4 K 164.9 K 147.5 K
0.005Rl 493.2 K 348.7 K 248.7 K 246.6 K 220.6 K
0.01Rl 586.5 K 414.7 K 338.6 K 293.3 K 262.3 K

Equilibrium Temperature for W.jpg

Ti

Equilibrium temperature for Ti, unit is K. (Melting point of Ti is 1941K)

2(mm) 4(mm) 6(mm) 8(mm) 10(mm)
0.001Rl 433.4 K 306.5 K 250.2 K 216.7 K 193.8 K
0.005Rl 648.1 K 458.3 K 374.2 K 324.0 K 289.8 K
0.01Rl 770.7 K 545.0 K 445.0 K 385.4 K 344.7 K

Equilibrium Temperature for Ti.jpg

Fe

Equilibrium temperature for Fe, unit is K. (Melting point of Fe is 1811 K)

2(mm) 4(mm) 6(mm) 8(mm) 10(mm)
0.001Rl 415.2 K 293.6 K 239.7 K 207.6 K 185.7 K
0.005Rl 620.8 K 439.0 K 358.4 K 310.4 K 277.6 K
0.01Rl 738.3 K 522.1 K 426.3 K 369.2 K 330.2 K

Equilibrium Temperature for Fe.jpg


5. Results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width )

Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of 0.00001, 0.0005 and 0.0001 times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm.

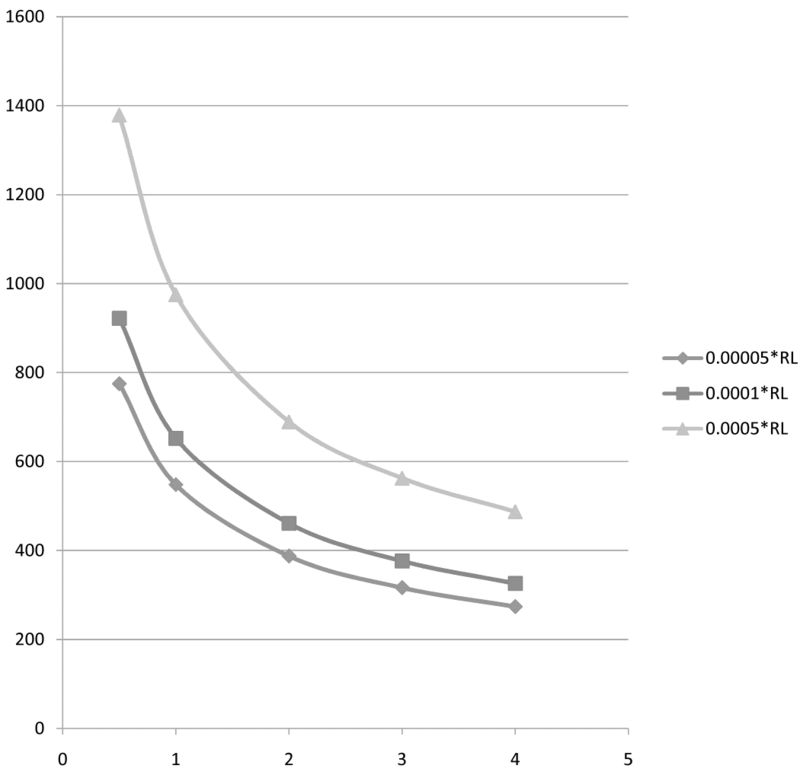
Al

Equilibrium temperature for Al, unit is K. (Melting point of Al is 933K)

1(mm) 2(mm) 3(mm) 4(mm)
0.00005Rl 548 K 387 K 317 K 274 K
0.0001Rl 652 K 461 K 376 K 326 K
0.0005Rl 975 K 689 K 562 K 487 K

down


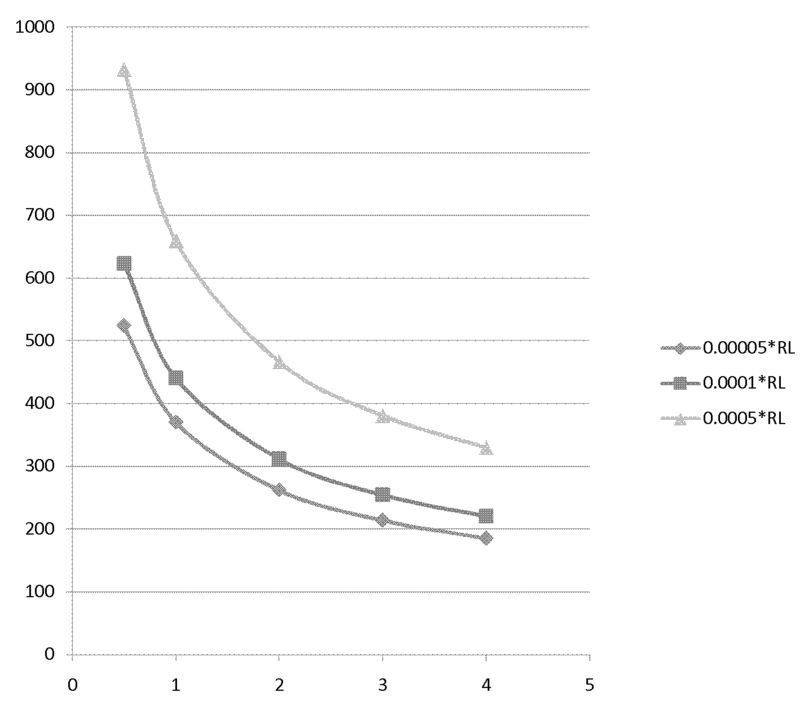
W

Equilibrium temperature for W, unit is K. (Melting point of Al is 3695K)

1(mm) 2(mm) 3(mm) 4(mm)
0.00005Rl 370 K 262 K 214 K 158 K
0.0001Rl 441 K 312 K 254 K 220 K
0.0005Rl 660 K 446 K 381 K 330 K

down


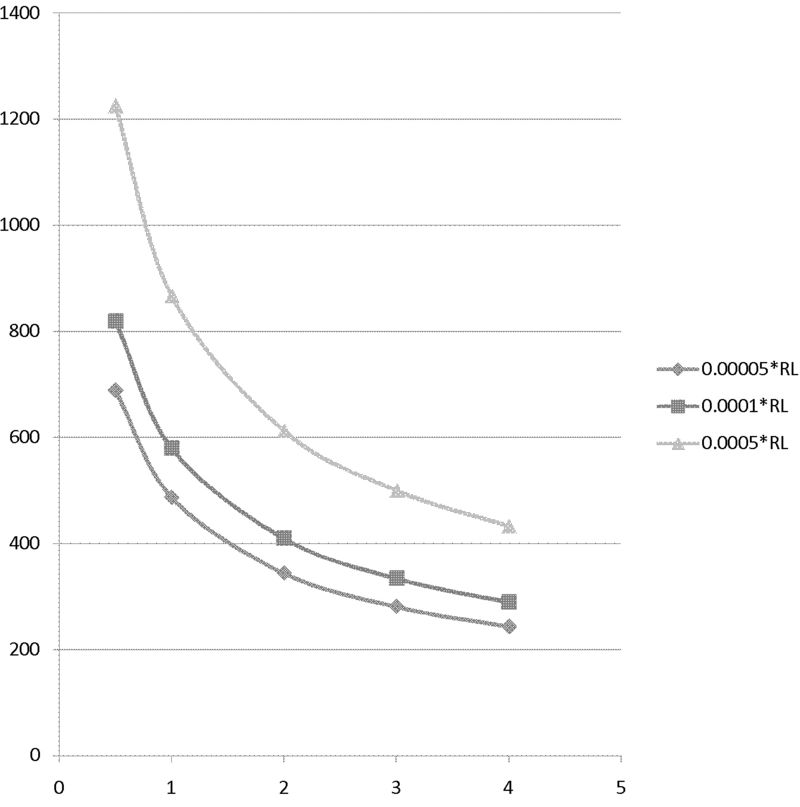
Ti

Equilibrium temperature for Ti, unit is K. (Melting point of Ti is 1941K)

1(mm) 2(mm) 3(mm) 4(mm)
0.00005Rl 487 K 334 K 281 K 244 K
0.0001Rl 597 K 410 K 335 K 290 K
0.0005Rl 1226 K 867 K 500 K 433 K

down


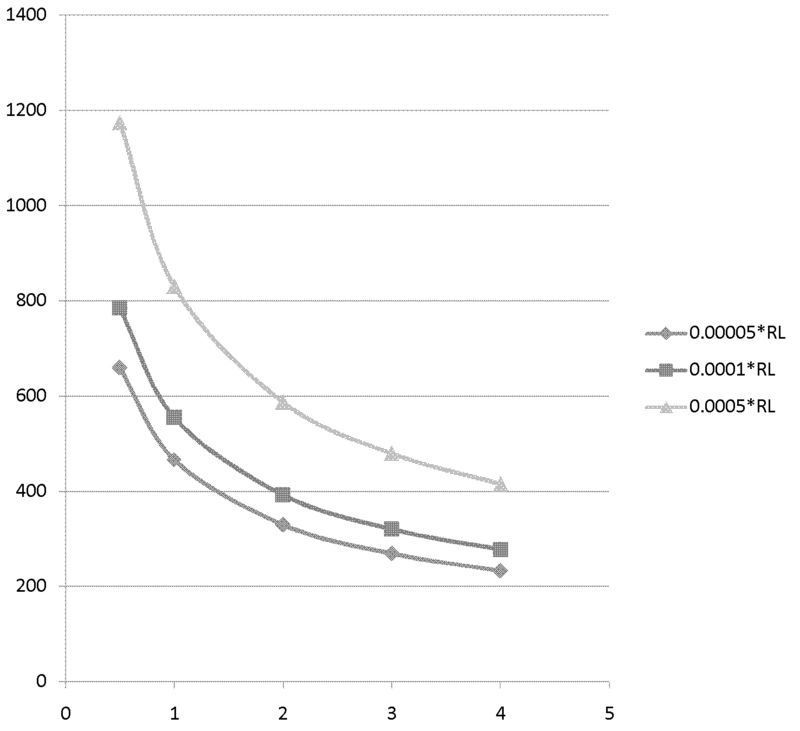
Fe

Equilibrium temperature for Fe, unit is K. (Melting point of Fe is 1811 K)

1(mm) 2(mm) 3(mm) 4(mm)
0.00005Rl 467 K 330 K 270 K 233 K
0.0001Rl 555 K 393 K 321 K 278 K
0.0005Rl 830 K 587 K 479 K 415 K

down


6. More results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width for Θ₀ = 0.2,0.4,0.6 dgrees)

Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of [math]3.9*10^{-5}[/math] (Θ₀ = [math]0.2^{o}[/math]), [math]1.35*10^{-4}[/math](Θ₀= [math]0.4^{o}[/math]) and [math]2.8*10^{-4}[/math](Θ₀ = [math]0.6^{o}[/math]) times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm.

Al

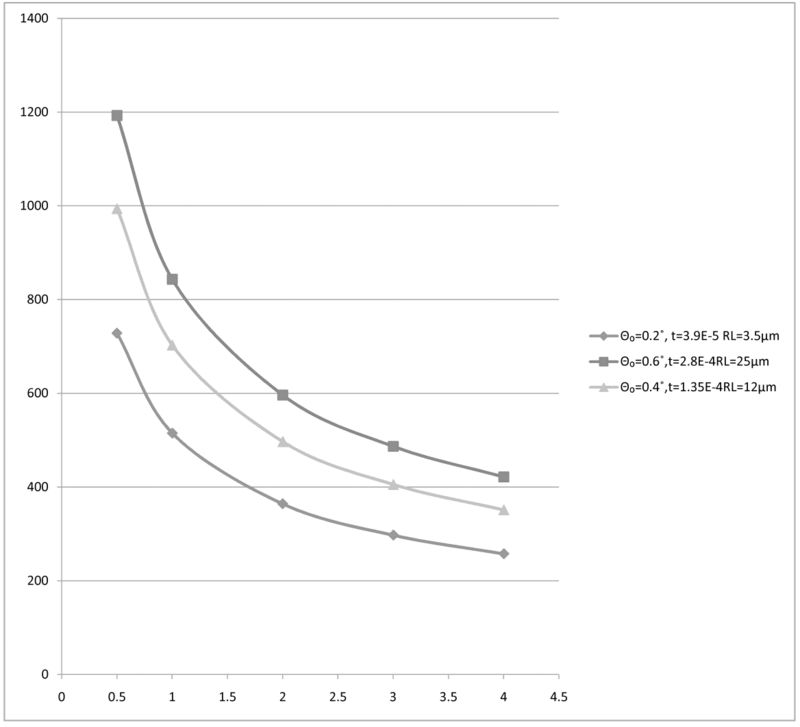
Equilibrium temperature for Al, unit is K. (Melting point of Al is 933K)

2(mm) 3(mm) 4(mm)
Θ₀=0.2˚, t=3.9E-5 RL=3.5μm 364 K 298 K 258 K
Θ₀=0.4˚,t=1.35E-4RL=12μm 497 K 406 K 351 K
Θ₀=0.6˚,t=2.8E-4RL=25μm 596 K 487 K 422 K

down

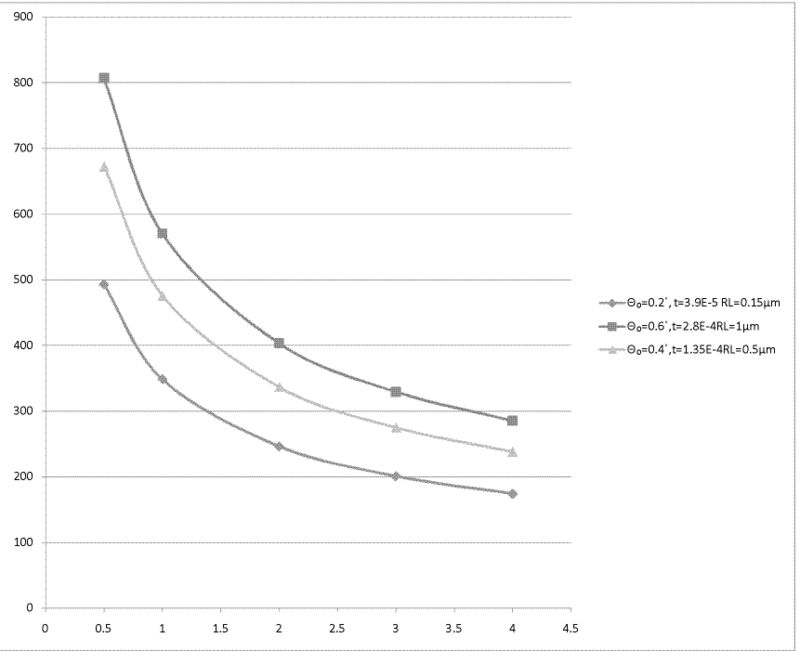
W

Equilibrium temperature for W, unit is K. (Melting point of Al is 3695K)

2(mm) 3(mm) 4(mm)
Θ₀=0.2˚, t=3.9E-5 RL=0.15μm 246 K 201 K 174 K
Θ₀=0.4˚,t=1.35E-4RL=0.5μm 336 K 275 K 237 K
Θ₀=0.6˚,t=2.8E-4RL=1μm 404 K 329 K 285 K


down

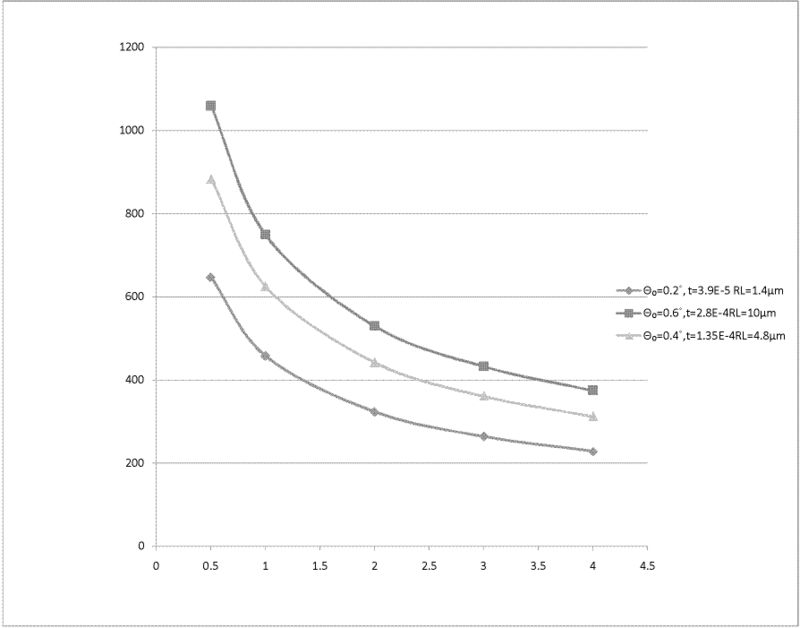
Ti

Equilibrium temperature for Ti, unit is K. (Melting point of Ti is 1941K)


2(mm) 3(mm) 4(mm)
Θ₀=0.2˚, t=3.9E-5 RL=1.4μm 329 K 264 K 229 K
Θ₀=0.4˚,t=1.35E-4RL=4.8μm 442 K 360 K 312 K
Θ₀=0.6˚,t=2.8E-4RL=10μm 530 K 432 K 375 K

down

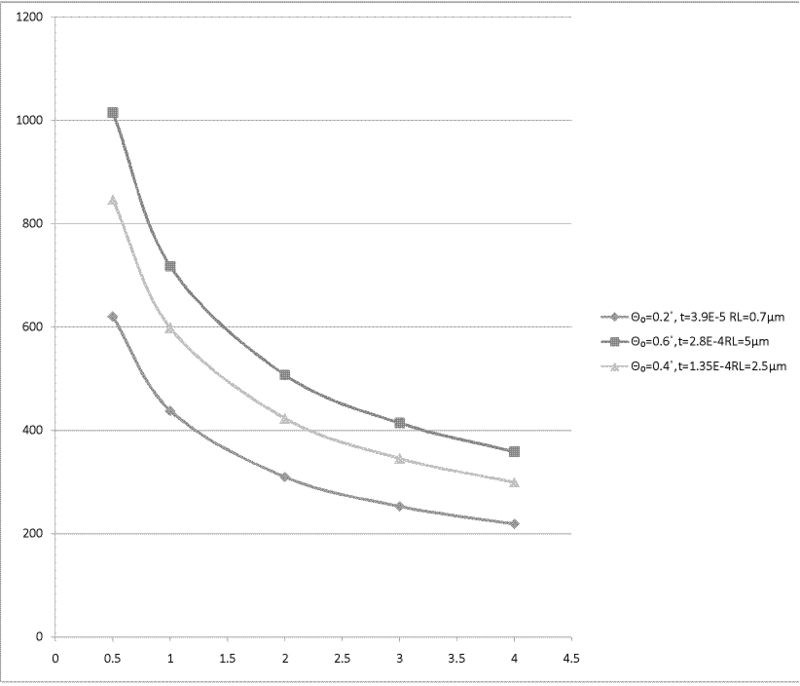
Fe

Equilibrium temperature for Fe, unit is K. (Melting point of Fe is 1811 K)


2(mm) 3(mm) 4(mm)
Θ₀=0.2˚, t=3.9E-5 RL=0.7μm 310 K 253 K 219 K
Θ₀=0.4˚,t=1.35E-4RL=2.5μm 423 K 346 K 299 K
Θ₀=0.6˚,t=2.8E-4RL=5μm 508 K 415 K 359 K

down

Go Back

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Radiators_Temperature&oldid=32416"