Difference between revisions of "LB SageBrushWork PostDefense"

From New IAC Wiki
Jump to navigation Jump to search
 
(263 intermediate revisions by 2 users not shown)
Line 273: Line 273:
  
 
740-1020 (Mixture)
 
740-1020 (Mixture)
 +
 +
The histogram representing the time cuts for the third run are shown below
 +
 +
It would appear that first two time cuts are difficult to determine because the Co-60 flag's counts are on the same order as the sample's, so watch out for this next time! Each run should be roughly 300 seconds for the sample and 60 seconds for the Co-60 flag, so check the histograms to make sure there are no Co-60 lines to correct for this. To double check these time cuts I looked for Cl-34m in the mixture (which according to my 10% analysis was not present in the pure Se sample) and the Co-60 lines that may have overlapped. It seems there is a line near 1773 keV present in the mixture, but the 1332 keV line is missing in the mixture. Keep an eye out.
 +
 +
[[File:0 04Percent SeSage TimeCuts 1DHistogram Run3.png|200px]]
 +
 +
0-300 (Mixture,145 keV 1173 present | 1332 keV not present,good)
 +
 +
305-350 (Co-60, good)
 +
 +
360-650 (Pure Se, good)
 +
 +
660-710 (Co-60, good)
 +
 +
720-940 (Mixture, good)
 +
 +
1020-1070 (Co-60, good)
 +
 +
1100-1240 (Pure Se, good)
 +
 +
1270-1310 (Co-60, good)
 +
 +
1320-1630 (Mixture, good)
 +
 +
1660-1720 (Co-60, good)
 +
 +
1740-2030 (Pure Se, good)
 +
 +
2040-2120 (Co-60, good)
 +
 +
2130-2420 (Mixture, good)
 +
 +
2430-2490 (Co-60, good)
 +
 +
2500-2800 (Pure Se, good)
 +
 +
2810-2850 (Co-60, good)
 +
 +
2880-3150 (Mixture, good)
 +
 +
3170-3220 (Co-60, good)
 +
 +
3240-3510 (Pure Se, good)
 +
 +
3520-3580 (Co-60, good)
 +
 +
3600-3970 (Mixture, good)
 +
 +
4000-4060 (Co-60, good)
 +
 +
4100-4350 (Pure Se, good)
 +
 +
4370-4420 (Co-60, good)
 +
 +
4450-4710 (Mixture, good)
 +
 +
4730-4780 (Co-60, good)
 +
 +
4800-5080 (Pure Se, good)
 +
 +
5100-5160 (Co-60, good)
 +
 +
5190-5460 (Mixture)
 +
 +
5410-5600 (Co-60)
 +
 +
Below is the histogram representing the time cuts for the 4th run
 +
 +
[[File:0 04Percent SeSage TimeCuts 1DHistogram Run4.png|200px]]
 +
 +
Below are the time cuts
 +
 +
0-300 (Pure Se)
 +
 +
306-359 (Co-60)
 +
 +
362-818 (Mixture)
  
 
=Gamma Spectrum Analysis=
 
=Gamma Spectrum Analysis=
Line 336: Line 414:
 
||.Dat File Entry For HL Plot ||  
 
||.Dat File Entry For HL Plot ||  
 
|}
 
|}
 +
 +
===Background and SNR Information===
 +
Below is a plot of the background in a 10 channel window around the short lived half life's energy peak of interest (103 keV). The long lived half live can be measured for at least a year even in a 0.1% by mass concentration, so it is less pressing. The values presented are weighted by the mass of the sage ash.
 +
 +
[[File:LB 10Percent OvenAshSeMix BackgroundExpoHL.png|200px]]
 +
 +
The fit parameters are
 +
 +
Constant:  4.50734e+00 +/- 2.42037e-03
 +
 +
Slope: -2.31438e-04 +/- 1.05610e-06
 +
 +
Which gives a rough half life of 49.92 +/- 0.23 minutes
 +
 +
Below is the SNR plotted in xmgrace
 +
 +
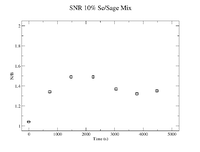
[[File:LB SNR 10Percent SeSageMix.png|200px]]
  
 
==0.1% Sample Analysis==
 
==0.1% Sample Analysis==
Line 391: Line 486:
 
||.Dat File Entry For HL Plot || -  || -  || - || -
 
||.Dat File Entry For HL Plot || -  || -  || - || -
 
|}
 
|}
 +
 +
===Background and SNR Information===
 +
Below is the information for the background in the window [109,119] (Channel # here). The data was weighted by both the runtime and the mass of the sage ash.
 +
 +
[[File:0 04Percent SageSeMixture BackgroundHL.png|200px]]
 +
 +
The fit parameters here are
 +
 +
Constant: 3.42624e+00 +/- 3.71043e-03
 +
 +
Slope: -3.44115e-04 +/- 7.67333e-07
 +
 +
which gives a half life of 33.57 +/- 0.07 minutes.
 +
 +
The SNR plot is shown below
 +
 +
[[File:LB 0 04Percent SNRPlot xmgrace.png|200px]]
  
 
=Fall 2018 Possible Sage Irradiation Activity Prediction=
 
=Fall 2018 Possible Sage Irradiation Activity Prediction=
Line 493: Line 605:
 
||Sage Ash || 9/11/18 || 14:59:50 || 10:57 || 71854.534 || 40 || Detector D || <1% || LB_SageAsh_OvenMethod_9_11_18_DetD_003
 
||Sage Ash || 9/11/18 || 14:59:50 || 10:57 || 71854.534 || 40 || Detector D || <1% || LB_SageAsh_OvenMethod_9_11_18_DetD_003
 
|-
 
|-
−
|| Sage Ash || 9/12/18 || 11:01:05 || || || 20 || Detector D || <1% || LB_SageAsh_OvenMethod_9_12_18_DetD_Pos20_001
+
|| Sage Ash || 9/12/18 || 11:01:05 || ||89908.033 || 20 || Detector D || <1% || LB_SageAsh_OvenMethod_9_12_18_DetD_Pos20_001
 +
|-
 +
|| Sage Ash || 9/13/18 || 12:03:02 || || 73275.295 || 10 || Det D || <1% || LB_SageAsh_OvenMethod_9_13_18_DetD_Pos10_001
 +
|-
 +
|| Sage Ash || 9/14/18 || 09:26:37 || 10:41 (9/17/18) || ||  10 || Det D || <1% || LB_SageAsh_OvenMethod_9_14_18_DetD_Pos10_001
 +
|-
 +
|| Sage Ash || 9/17/18 || 10:51:02 || || || 10 || Det D || <1% || LB_SageAsh_OvenMethod_9_17_18_DetD_Pos10_001
 +
|-
 +
|| Sage Ash || 10/01/18 ||14:04:00 || || || Face of Detector || Det D || <1% || LB_SageAsh_OvenMethod_10_1_18_DetD_DetFace_002
 
|-
 
|-
 
|}
 
|}
  
−
=Sage Background Analysis=
+
=September Sage+Al Analysis=
 +
 
 +
https://wiki.iac.isu.edu/index.php/MCNP_Sim_of_Jack_Converter
 +
 
 
Below is the first measured histogram generated from the file LB_SageAsh_OvenMethod_9_10_18_DetD_002. Note that the Al cylinder and the sage ash were not separated, so there will be some lines from Al present. The histogram shown below is not weighted because there are two different samples in front of the detector at the same time (Al cylinder and sage ash). Once the lines have been identified, the mass will be taken into account
 
Below is the first measured histogram generated from the file LB_SageAsh_OvenMethod_9_10_18_DetD_002. Note that the Al cylinder and the sage ash were not separated, so there will be some lines from Al present. The histogram shown below is not weighted because there are two different samples in front of the detector at the same time (Al cylinder and sage ash). Once the lines have been identified, the mass will be taken into account
  
Line 524: Line 647:
  
 
{| border="3"  cellpadding="5" cellspacing="0"
 
{| border="3"  cellpadding="5" cellspacing="0"
−
|| Histogram Line || Channel || Energy (keV) || Relative Rate (<math> \frac{A_2}{A_1} </math>)
+
|| Line Seen (keV) || Isotope
 +
|-
 +
||846 || Mn-56
 
|-
 
|-
−
||863 || 1726.8 || 846 || 0
+
|| 1810 || Mn-56
 +
|-
 +
|| 2133 || Mn-56
 +
|-
 +
||1368 || Na-24
 +
|-
 +
||2754 || Na-24
 +
|-
 +
|}
 +
 
 +
==Background Analysis==
 +
Below is the analysis of the background around the Se line of interest. The histograms were unweighted due to the presence of both the Al cylinder and the sage ash. The data points on the half life plot are weighted by the runtime. The energy window used was [90,130]. The times I concerned myself with spanned 5 half lives of Se (17184 sec) which were split cut into 10 different sets (runtime = 1718.4 sec).
 +
 
 +
The parameters are as follows
 +
 
 +
 
 +
{| border="3"  cellpadding="5" cellspacing="0"
 +
|| || 0<t<1718.4 s || 1718.4<t<3436.8 s || 3436.8<t<5155.2 s || 5155.2<t<6873.6 s || 6873.6<t<8592 s || 8592<t<10310.4 s || 10310.4<t<12028.8 s || 12028.8<t<13747.2 s || 13747.2<t<15461.6 s ||  15461.6<t<17180 s
 
|-
 
|-
−
||1846 || 3692 || 1810 || 0
+
|| Slope (<math> \alpha </math>) || 5.853 <math> \pm </math> 0.562 || 5.33 <math> \pm </math> 0.54 || 4.981 <math> \pm </math> 0.532 || 5.423 <math> \pm </math> 0.521 || 6.234 <math> \pm </math> 0.511 || 5.155 <math> \pm </math> 0.503 || 4.703 <math> \pm </math> 0.496 || 4.053 <math> \pm </math> 0.489 || 4.49 <math> \pm </math> 0.49 || 4.506 <math> \pm </math> 0.503   
 
|-
 
|-
−
||2155 || 4310.8 || 2133.4 || 0
+
|| Intercept (<math> \beta </math> ) || 1051 <math> \pm </math> 61.9 || 998.8 <math> \pm </math> 59.6 || 974.6 <math> \pm </math> 58.7 || 871.7 <math> \pm </math> 57.4 || 731.4 <math> \pm </math> 56.2 || 796.7 <math> \pm </math> 55.4 || 807.3 <math> \pm </math> 54.6 || 841 <math> \pm </math> 53.9 || 836.8 <math> \pm </math> 54.5 || 868.6 <math> \pm </math> 55.4
 +
|-
 +
||Integral from [90,130] || 39.45 <math> \pm </math> 2.04 || 36.90 <math> \pm </math> 1.96 || 35.44 <math> \pm </math> 1.92 || 34.18 <math> \pm </math> 1.89 || 32.99 <math> \pm </math> 1.85 || 31.74 <math> \pm </math> 1.82 || 30.83 <math> \pm </math> 1.80 || 29.95 <math> \pm </math> 1.77 || 30.98 <math> \pm </math> 1.78 || 31.76 <math> \pm </math> 1.82
 
|-
 
|-
 
|}
 
|}
  
−
===846 keV Line Analysis===
+
 
 +
 
 +
Now the total background was found by integrating the linear fit function across the region of interest, in other words
 +
 
 +
<math> f(x) = \int_a^b (\alpha x + \beta)dx </math>
 +
 
 +
To find the error in the integral, use the standard error propagation method
 +
 
 +
<math> \sigma_f = \sqrt{(\frac{\partial f}{\partial \alpha})^2 \sigma_{\alpha}^2 + (\frac{\partial f}{\partial \beta})^2 \sigma_{\beta}^2} </math>
 +
 
 +
<math> = \sqrt{[\frac{\partial}{\partial \alpha}(\int_a^b (\alpha x + \beta)dx)]^2 \sigma_{\alpha}^2 + [\frac{\partial}{\partial \beta}(\int_a^b (\alpha x + \beta)dx)]^2 \sigma_{\beta}^2} </math>
 +
 
 +
Since the partial derivatives are not taken with respect to the variable of integration and the function is analytic within the region, the derivative may be moved inside the integral. This action yields
 +
 
 +
<math>\sigma_f = \sqrt{(\int_a^b x dx)^2 \sigma_{\alpha}^2 + (\int_a^b dx)^2 \sigma_{\beta}^2} </math>
 +
 
 +
<math> = \sqrt{(\frac{b^2-a^2}{2})^2 \sigma_{\alpha}^2 + (b-a)^2 \sigma_{\beta}^2} </math>
 +
 
 +
 
 +
Below is the initial plot of the background in the region from [90,130]
 +
 
 +
[[File:LB Sept2018 Sage Al BackgroundHL InitialPlot.png|200px]]
 +
 
 +
This plot has some outliers and fluctuations in the background that could be due to the presence of other sources (Dr. Dale was measuring very hot gallium on Det A during my overnight measurement).
 +
 
 +
===10 Channel Analysis===
 +
The fits were done in a larger window [90,130] to get enough bins for a good fit, so I should be able to simply change the bounds of the integration to make the correction. There is definitely some randomness within the time cuts which produce bins with data above and below the fit line, which makes this more difficult. With the dithering, the peak on Detector A has a mean value of 103.949 kev, so the window I will analyze on Detector D (calibrated to energy) will be [99,109] keV
 +
 
 +
 
 +
{| border="3"  cellpadding="5" cellspacing="0"
 +
|| || 0<t<1718.4 s || 1718.4<t<3436.8 s || 3436.8<t<5155.2 s || 5155.2<t<6873.6 s || 6873.6<t<8592 s || 8592<t<10310.4 s || 10310.4<t<12028.8 s || 12028.8<t<13747.2 s || 13747.2<t<15461.6 s ||  15461.6<t<17184 s || 17184 <t< 18902.4 s  || 18902.4 <t< 20620.8 s || 20620.8<t<22339.2 s || 22339.2<t<24057.6 s || 24057.6<t<25776 s  || 25776<t<27494.4 s || 27494.4<t<29212.8 s || 29212.8 <t< 30931.2 s || 30931.2 <t< 32649.6 s || 32649.6<t<34368 s || 34368<t<36086.4 s || 36086.4<t<37804.8 || 37804.8 <t< 39523.2 || 39523.2<t<41241.6 s || 41241.6 <t< 42960 s || 42960<t<44678.4 s || 44678.4 <t< 46396.8 s
 +
|-
 +
|| Slope (<math> \alpha </math>) || 5.853 <math> \pm </math> 0.562 || 5.33 <math> \pm </math> 0.54 || 4.981 <math> \pm </math> 0.532 || 5.423 <math> \pm </math> 0.521 || 6.234 <math> \pm </math> 0.511 || 5.155 <math> \pm </math> 0.503 || 4.703 <math> \pm </math> 0.496 || 4.053 <math> \pm </math> 0.489 || 4.49 <math> \pm </math> 0.49 || 4.506 <math> \pm </math> 0.503 || 5.101 <math> \pm </math> 0.496 || 5.215 <math> \pm </math> 0.490 || 4.695 <math> \pm </math> 0.482 || 4.685 <math> \pm </math> 0.477 || 4.731 <math> \pm </math> 0.468 || 4.218 <math> \pm </math> 0.468 || 3.95 <math> \pm </math> 0.459  || 4.388 <math> \pm </math> 0.452 || 4.180 <math> \pm </math> 0.446 || 3.512 <math> \pm </math> 0.442 || 4.423 <math> \pm </math> 0.440 || 4.751 <math> \pm </math> 0.435 || 3.695 <math> \pm </math> 0.431 || 3.372 <math> \pm </math> 0.424 || 3.112 <math> \pm </math> 0.420 || 3.784 <math> \pm </math> 0.415 || 2.792 <math> \pm </math> 0.414
 +
|-
 +
|| Intercept (<math> \beta </math> ) || 1051 <math> \pm </math> 61.9 || 998.8 <math> \pm </math> 59.6 || 974.6 <math> \pm </math> 58.7 || 871.7 <math> \pm </math> 57.4 || 731.4 <math> \pm </math> 56.2 || 796.7 <math> \pm </math> 55.4 || 807.3 <math> \pm </math> 54.6 || 841 <math> \pm </math> 53.9 || 836.8 <math> \pm </math> 54.5 || 868.6 <math> \pm </math> 55.4 || 769.5 <math> \pm </math> 54.6 || 732.8 <math> \pm </math> 54.0 || 737.5 <math> \pm </math> 53.1 || 715.1 <math> \pm </math> 52.6 || 673.8 <math> \pm </math> 51.6 || 714.3 <math> \pm </math> 51.5 || 701.0 <math> \pm </math> 50.6 || 625.5 <math> \pm </math> 49.8 || 620.9 <math> \pm </math> 49.1 || 676.1 <math> \pm </math> 48.8 || 562.8 <math> \pm </math> 48.4 || 508.3 <math> \pm </math> 47.9 || 600.2 <math> \pm </math> 47.5 || 608 <math> \pm </math> 46.7 || 623 <math> \pm </math> 46.3 || 519.5 <math> \pm </math> 45.7 || 618.1 <math> \pm </math> 45.6
 +
|-
 +
||Fit Function Integral from [99,109] || 9.67 <math> \pm </math> 0.50 || 9.04 <math> \pm </math> 0.48  ||  8.69 <math> \pm </math> 0.47 || 8.35 <math> \pm </math> 0.46 || 8.03 <math> \pm </math> 0.45 || 7.76 <math> \pm </math> 0.44 ||  7.54 <math> \pm </math> 0.44 || 7.35 <math> \pm </math> 0.43 || 7.59 <math> \pm </math> 0.43 || 7.78 <math> \pm </math> 0.44 || 7.57 <math> \pm </math> 0.44 || 7.42 <math> \pm </math> 0.43 || 7.13 <math> \pm </math> 0.42 || 7.00 <math> \pm </math> 0.42 || 6.78 <math> \pm </math> 0.41 || 6.71 <math> \pm </math> 0.41 || 6.47 <math> \pm </math> 0.40 || 6.30 <math> \pm </math> 0.40 || 6.14 <math> \pm </math> 0.39 || 6.06 <math> \pm </math> 0.39 || 5.95 <math> \pm </math> 0.39 || 5.83 <math> \pm </math> 0.38 || 5.73 <math> \pm </math> 0.38 || 5.58 <math> \pm </math> 0.37 || 5.51 <math> \pm </math> 0.37 || 5.31 <math> \pm </math> 0.37 || 5.29 <math> \pm </math> 0.36   
 +
|-
 +
||Stats Box Integral || <math> 1.674 \times 10^4 </math> || <math> 1.565 \times 10^4 </math> || <math> 1.505 \times 10^4 </math> ||  <math> 1.159 \times 10^4 </math> || <math> 1.401 \times 10^4 </math> ||  <math> 1.341 \times 10^4 </math> || <math> 1.306 \times 10^4 </math> || <math> 1.292 \times 10^4 </math> || <math> 1.332 \times 10^4 </math> || <math> 1.347 \times 10^4 </math> || <math> 1.313 \times 10^4 </math> || <math> 1.296 \times 10^4 </math> || <math> 1.238 \times 10^4 </math> || <math> 1.197 \times 10^4 </math> || <math> 1.194 \times 10^4 </math> || <math> 1.166 \times 10^4 </math> || <math> 1.134 \times 10^4 </math> || <math> 1.101 \times 10^4 </math>  || <math> 1.085 \times 10^4 </math> || <math> 1.064 \times 10^4 </math> || <math> 1.046 \times 10^4 </math> || <math> 1.027 \times 10^4 </math> || 9943 || 9872 || 9699 || 9206 || 9110
 +
|-
 +
||Stats Box Activity (Hz) || 9.58 <math> \pm </math> 0.07 || 9.12 <math> \pm </math> 0.07 || 8.76 <math> \pm </math> 0.07 || 6.74 <math> \pm </math> 0.06 || 8.15 <math> \pm </math> 0.07 || 7.80 <math> \pm </math> 0.07 || 7.60 <math> \pm </math> 0.07 || 7.53 <math> \pm </math> 0.07 || 7.75 <math> \pm </math> 0.07 || 7.84 <math> \pm </math> 0.07 || 7.64 <math> \pm </math> 0.07 || 7.54 <math> \pm </math> 0.07 || 7.20 <math> \pm </math> 0.06 || 6.97 <math> \pm </math> 0.06 || 6.95 <math> \pm </math> 0.06 || 6.79 <math> \pm </math> 0.06 || 6.60 <math> \pm </math> 0.06 || 6.41 <math> \pm </math> 0.06 || 6.31 <math> \pm </math> 0.06 || 6.19 <math> \pm </math> 0.06 || 6.09 <math> \pm </math> 0.06 || 5.98 <math> \pm </math> 0.06 || 5.79 <math> \pm </math> 0.06 || 5.74 <math> \pm </math> 0.06 || 5.64 <math> \pm </math> 0.06 || 5.36 <math> \pm </math> 0.06 || 5.30 <math> \pm </math> 0.06 
 +
|-
 +
||Corrected Background Measurement || 9.58 <math> \pm </math> 0.09 || 9.12 <math> \pm </math> 0.08 || 8.76 <math> \pm </math> 0.07 || 6.74 <math> \pm </math> 1.61 || 8.15 <math> \pm </math> 0.12 || 7.80 <math> \pm </math> 0.04 || 7.60 <math> \pm </math> 0.06 || 7.53 <math> \pm </math> 0.18 || 7.75 <math> \pm </math> 0.16 || 7.84 <math> \pm </math> 0.06 ||  7.64 <math> \pm </math> 0.07 || 7.54 <math> \pm </math> 0.12 || 7.20 <math> \pm </math> 0.07 || 6.97 <math> \pm </math> 0.03 || 6.95 <math> \pm </math> 0.17 || 6.79 <math> \pm </math> 0.08 || 6.60 <math> \pm </math> 0.13 || 6.41 <math> \pm </math>  || 6.31 <math> \pm </math> 0.17 || 6.19 <math> \pm </math> 0.13 || 6.09 <math> \pm </math> 0.14 || 5.98 <math> \pm </math> 0.15 || 5.79 <math> \pm </math> 0.06 || 5.74 <math> \pm </math> 0.16 || 5.64 <math> \pm </math> 0.13 || 5.36 <math> \pm </math> 0.05 || 5.30 <math> \pm </math> 0.01 
 +
|-
 +
|}
 +
 
 +
 
 +
[[File:LB Sept2018 Sage Al BackgroundHL InitialPlot 10Chan_Full.png|200px]]
 +
 
 +
This looks like there are two separate half lives present, so split them up and fit.
 +
 
 +
[[File:LB Sept2018 Sage Al BackgroundHL InitialPlot 10Chan FirstPortion.png|200px]]
 +
 
 +
The fit parameters for the first portion are
 +
 
 +
Slope: -2.22732e-05 +/- 8.61118e-07
 +
 
 +
Constant:2.25058e+00 +/- 6.19036e-03
 +
 
 +
Which gives a half life of 8.47 +/- 0.32 hours
 +
 
 +
[[File:LB Sept2018 Sage Al BackgroundHL InitialPlot 10Chan SecondPortion.png|200px]]
 +
 
 +
The fit parameters for the second portion are
 +
 
 +
Constant: 2.24079e+00 +/- 5.78712e-03
 +
 
 +
Slope: -1.28411e-05 +/- 1.46816e-07
 +
 
 +
Which gives a half life of 14.99 +/- 0.17 hours
 +
 
 +
==846 keV Line Analysis==
 
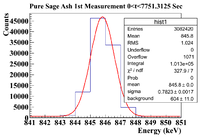
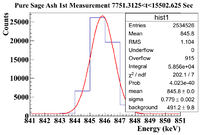
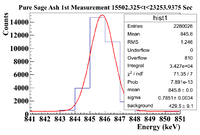
Below is the analysis table. The energy window under study is [841,851]
 
Below is the analysis table. The energy window under study is [841,851]
  
  
 
{| border="3"  cellpadding="5" cellspacing="0"
 
{| border="3"  cellpadding="5" cellspacing="0"
−
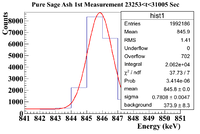
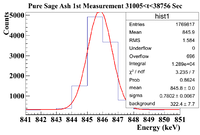
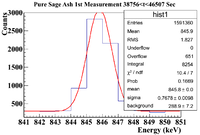
|| ||  0<t<7751.3125 || 7751.3125 <t< 15502.625 || 15502.325 <t< 23253.9375
+
|| ||  0<t<7751.3125 || 7751.3125 <t< 15502.625 || 15502.325 <t< 23253.9375 || 23253.9375 <t< 31005.25 || 31005.25 <t< 38756.5625 || 38756.5625 <t< 46507.875
 +
|-
 +
|| Histogram || [[File:PureSageAsh 1stMeasurement 0 t 7751Sec 846keVLine.png|200px]] || [[File:PureSageAsh 1stMeasurement 7751 t 15502Sec 846keVLine.png|200px]] || [[File:PureSageAsh 1stMeasurement 15502 t 23253Sec 846keVLine.png|200px]] || [[File:PureSageAsh 1stMeasurement 23253 t 31005Sec 846keVLine.png|200px]] || [[File:PureSageAsh 1stMeasurement 31005 t 38756Sec 846keVLine.png|200px]] || [[File:PureSageAsh 1stMeasurement 38756 t 46507Sec 846keVLine.png|200px]]
 +
|-
 +
||Signal in Window || 1.013 <math> \times 10^5 \pm </math> 318.28 || 5.856 <math> \times 10^4 \pm </math> 241.99 || 3.427 <math> \times 10^4 \pm </math> 185.12 || 2.062 <math> \times 10^4 \pm </math> 143.60 || 1.289 <math> \times 10^4 \pm </math> 113.53 || 8254 <math> \pm </math> 90.85
 +
|-
 +
||Integrated Background || 6040 <math> \pm </math> 110 || 4912 <math> \pm </math> 98 || 4295 <math> \pm </math> 91 || 3739 <math> \pm </math> 83 || 3224 <math> \pm </math> 77 || 2889 <math> \pm </math> 72
 +
|-
 +
||Signal - Background || 9.5260 <math> \times 10 ^4 \pm </math> 336.75 || 5.3648 <math> \times 10^4 \pm </math> 261.08 || 2.9975 <math> \times 10^4 \pm </math> 206.28 || 1.6881 <math> \times 10^4 \pm </math> 165.86 || 9666 <math> \pm </math> 137.18 || 5365 <math> \pm </math> 115.92
 +
|-
 +
||Runtime (s) ||  7751.3125 ||  7751.3125 || 7751.3125 || 7751.3125 || 7751.3125 || 7751.3125
 +
|-
 +
||Rate (Hz) ||12.29 <math> \pm </math> 0.04 || 6.92 <math> \pm </math> 0.03 || 3.87 <math> \pm </math> 0.03 || 2.18 <math> \pm </math> 0.02 || 1.25 <math> \pm </math> 0.02 || 0.69 <math> \pm </math> 0.01
 +
|-
 +
|}
 +
 
 +
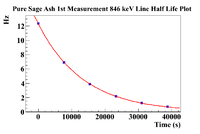
The exponential decay plot is shown below
 +
 
 +
[[File:PureSageAsh 1stMeasurement 846keVHL ExpoPlot.png|200px]]
 +
 
 +
 
 +
The fit parameters are
 +
 
 +
Constant: 2.50880 <math> \pm </math> 0.00287747
 +
 
 +
Slope: -7.42478 <math> \pm </math> 0.0249932 <math> \times 10^{-5} </math>
 +
 
 +
Which yields a half life of 2.59 <math> \pm </math> 0.01 hours, which is within one standard deviation of Mn-56's half life (2.58 hours)
 +
 
 +
The lines that are characteristic with the highest branching ratios of Mn-56 (1810,2133 keV) are both present in the spectrum. This would lead me to believe it is indeed Mn-56 which is produced by either a proton knockout of Fe-57, or neutron capture on Mn-55.
 +
 
 +
There is also an 834 keV line present, but due to the long half life of Mn-54, this will take some time to analyze, but remember it is there!
 +
 
 +
==1367.5 keV Line Analysis==
 +
There is a line decaying at 1367.5 keV. Let's do an analysis on it to see if the isotope can be identified. The window of analysis is [1362,1372]
 +
 
 +
 
 +
{| border="3"  cellpadding="5" cellspacing="0"
 +
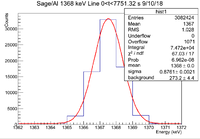
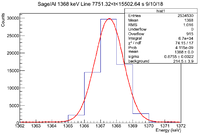
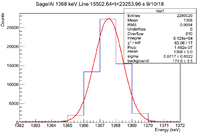
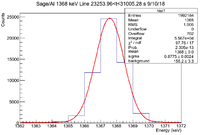
|| || 0<t<7751.32 s ||  7751.32<t<15502.64 s || 15502.64<t<23253.96 s || 23253.96<t<31005.28 s || 31005.28<t<38756.6 s || 38756.6<t<46507.9 s
 
|-
 
|-
−
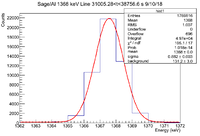
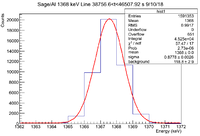
|| Histogram || [[File:PureSageAsh 1stMeasurement 0 t 7751Sec 846keVLine.png|200px]] || [[File:PureSageAsh 1stMeasurement 7751 t 15502Sec 846keVLine.png|200px]]
+
|| Histogram || [[File:LB SageAl 1368keV 0 t 7751 9 10 18.png|200px]] || [[File:LB SageAl 1368keV 7751 t 15502 9 10 18.png|200px]] || [[File:LB SageAl 1368keV 15502 t 23253 9 10 18.png|200px]] || [[File:LB SageAl 1368keV 23253 t 31005 9 10 18.png|200px]] || [[File:LB SageAl 1368keV 31005 t 38756 9 10 18.png|200px]] || [[File:LB SageAl 1368keV 38756 t 46507 9 10 18.png|200px]]
 
|-
 
|-
−
||Signal in Window || 1.013 <math> \times 10^5 \pm </math> 318.28 || 5.856 <math> \times 10^4 \pm </math> 241.99 || 3.427 <math> \times 10^4 \pm </math> 185.12
+
||Signal in Window || <math> 7.472 \times 10^4 </math> || <math> 6.7 \times 10^4 </math> || <math> 6.129 \times 10^4 </math> || <math> 5.567 \times 10^4 </math> || <math> 4.97 \times 10^4 </math> || <math> 4.525 \times 10^4 </math>
 
|-
 
|-
−
||Integrated Background || 6040 <math> \pm </math> 110 || 4912 <math> \pm </math> 98 || 4295 <math> \pm </math> 91
+
||Integrated Background || 2732 <math> \pm </math> 44 || 2145 <math> \pm </math> 39 || 1746 <math> \pm </math> 35 || 1552 <math> \pm </math> 33 || 1312 <math> \pm </math> 30 || 1188 <math> \pm </math> 29
 
|-
 
|-
−
||Signal - Background || 9.5260 <math> \times 10 ^4 \pm </math> 336.75 || 5.3648 <math> \times 10^4 \pm </math> 261.08 || 2.9975 <math> \times 10^4 \pm </math> 206.28
+
||Signal - Background || 71988 <math> \pm </math> 276.868 || 64855 <math> \pm </math> 261.765 || 59544 <math> \pm </math> 250.03 || 54118 <math> \pm </math> 238.241 || 48388 <math> \pm </math> 224.944 || 44062 <math> \pm </math> 214.688
 
|-
 
|-
−
||Runtime (s) || 7751.3125 || 7751.3125 || 7751.3125
+
||Runtime (s) || 7751.32 || 7751.32 || 7751.32 || 7751.32 || 7751.32 || 7751.3
 
|-
 
|-
−
||Rate (Hz) ||12.29 <math> \pm </math> 0.04 || 6.92 <math> \pm </math> 0.03 || 3.87 <math> \pm </math> 0.03
+
||Rate (Hz) || 9.29 <math> \pm </math> 0.04 || 8.37 <math> \pm </math> 0.03 || 7.68 <math> \pm </math> 0.03 || 6.98 <math> \pm </math> 0.03 || 6.24 <math> \pm </math> 0.03 || 5.68 <math> \pm </math> 0.03 ||   
 
|-
 
|-
 
|}
 
|}
 +
 +
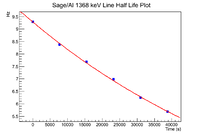
[[File:LB SageAL 1368keV HalfLifePlot.png|200px]]
 +
 +
The fit parameters are
 +
 +
constant: 2.22835e+00 +/- 2.95795e-03
 +
 +
slope: -1.26126e-05 +/- 1.41004e-07
 +
 +
which gives a half life of 15.26 +/- 0.17 hours. This is within 2 standard deviations of Na-24's half life. This isotope also has a line present at 2754 keV, which is present in the energy spectrum. Also this is the only isotope with branching ratios compatible with the gamma spectrum data. This would be a neutron capture on stable Na-23.
 +
 +
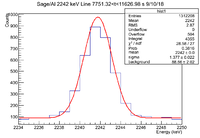
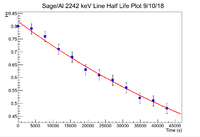
==2242 keV Analysis==
 +
There is a decaying line seen at 2242 keV. The analysis was done in a 16 channel window from [2234,2250]
 +
 +
{| border="3"  cellpadding="5" cellspacing="0"
 +
|| || 0<t<3875.66 s || 3875.66<t<7751.32 s || 7751.32<t<11626.98 s || 11626.98<t<15502.64 s || 15502.64<t<19378.3 s || 19378.3<t<23253.96 s || 23253.96<t<27129.62 s || 27129.62<t<31005.28 s || 31005.28<t<34880.94 s || 34880.94<t<38756.6 s || 38756.6<t<42632.26 s || 42632.26<t<46507.9 s
 +
 +
|-
 +
|| Histogram || [[File:LB SageAl 2242keVLine 0 t 3875.66 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 3875.66 t 7751.32 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 7751 t 11626 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 11626 t 15502 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 15502 t 19378 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 19378 t 23253 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 23253 t 27129 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 27129 t 31005 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 31005 t 34880 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 34880 t 38756 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 38756 t 42632 9 10 18.png|200px]] || [[File:LB SageAl 2242keVLine 42632 t 46507 9 10 18.png|200px]]
 +
|-
 +
||Signal in Window || 4792 || 4625 || 4355 || 4124 || 3975 || 3759 || 3498 || 3479 || 3280 || 3041 || 2945 || 2807
 +
|-
 +
||Integrated Background ||1686.4 <math> \pm </math> 35.2 || 1567.36 <math> \pm </math> 33.76 || 1418.56 <math> \pm </math> 32.32 || 1355.68 <math> \pm </math> 31.52 || 1347.52 <math> \pm </math> 31.2 || 1300 <math> \pm </math> 30.72 || 1152.48 <math> \pm </math> 29.12  || 1198.24 <math> \pm </math> 29.44 || 1111.36 <math> \pm </math> 28.48 || 1012.48 <math> \pm </math> 27.36 || 969.6 <math> \pm </math> 27.2 || 925.76 <math> \pm </math> 26.08
 +
|-
 +
||Signal - Background || 3105.6 <math> \pm </math> 77.66 || 3057.64 <math> \pm </math> 75.93 || 2936.44 <math> \pm </math> 73.48 || 2768.32 <math> \pm </math> 71.54 || 2627.48 <math> \pm </math> 70.35 || 2459 <math> \pm </math> 68.58 || 2345.52 <math> \pm </math> 65.92 || 2280.76 <math> \pm </math> 65.92 || 2168.64 <math> \pm </math> 63.96 || 2028.52 <math> \pm </math> 61.56 || 1975.4 <math> \pm </math> 60.70 || 1881.24 <math> \pm </math> 59.05
 +
|-
 +
||Runtime (s) ||  3875.66 ||  3875.66 || 3875.66 || 3875.66 || 3875.66 || 3875.66 || 3875.66 || 3875.66 ||  3875.66 || 3875.66 || 3875.66 ||  3875.64
 +
|-
 +
||Rate (Hz) || 0.80 <math> \pm </math> 0.02 || 0.79 <math> \pm </math> 0.02 || 0.76 <math> \pm </math> 0.02 || 0.71 <math> \pm </math> 0.02 || 0.68 <math> \pm </math> 0.02 || 0.63 <math> \pm </math> 0.02 || 0.61 <math> \pm </math> 0.02 || 0.59 <math> \pm </math> 0.02 || 0.56 <math> \pm </math> 0.02 || 0.52 <math> \pm </math> 0.02 || 0.51 <math> \pm </math> 0.02 || 0.48 <math> \pm </math> 0.02
 +
|-
 +
|}
 +
 +
[[File:LB 2242keVLine HLPlot.png|200px]]
 +
 +
The fit parameters are
 +
 +
Constant: -1.99924e-01 +/- 1.47295e-02
 +
 +
Slope: -1.24500e-05 +/- 6.90105e-07
 +
 +
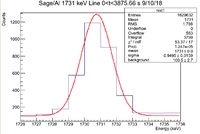
==1731 keV Analysis==
 +
There is a decaying line seen at 1731 keV in the Sage/Al samples from 9/10/18. The analysis was done in a 10 channel window from [1726,1736]
 +
 +
{| border="3"  cellpadding="5" cellspacing="0"
 +
|| || 0<t<3875.66 s || 3875.66<t<7751.32 s || 7751.32<t<11626.98 s || 11626.98<t<15502.64 s || 15502.64<t<19378.3 s || 19378.3<t<23253.96 s || 23253.96<t<27129.62 s || 27129.62<t<31005.28 s || 31005.28<t<34880.94 s || 34880.94<t<38756.6 s || 38756.6<t<42632.26 s || 42632.26<t<46507.9 s
 +
 +
|-
 +
||Histogram|| [[File:LB SageAl 1731keV 0 3875s 9 10 18.png|200px]]
 +
|-
 +
||Signal in Window || 3799 ||
 +
|-
 +
||Integrated Background || 1005 +/- 27
 +
|-
 +
||Signal - Background ||
 +
|-
 +
||Runtime (s) || 3875.66 ||  3875.66 || 3875.66 || 3875.66 || 3875.66 || 3875.66 || 3875.66 || 3875.66 ||  3875.66 || 3875.66 || 3875.66 ||  3875.64
 +
|-
 +
||Rate (Hz) ||
 +
|-
 +
|}
 +
 +
=Production Optimization=
 +
The sage ash has a density of 0.1977 <math> \frac{g}{cm^3} </math>. To perform this I will use an 8 hour half life from the sage ash/Al sample irradiated on 9/10/18.
 +
 +
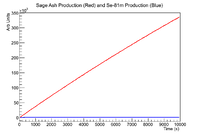
==8 Hour Half Life (9/10/18)==
 +
This section focuses on optimization for the sage/Al cylinder 8 hour half life performed above. The decay constant for that sample was -2.22732e-05 +/- 8.61118e-07 <math> s^{-1} </math>. The production rate is given by
 +
 +
<math> N(t) = \frac{n_T V_T}{\lambda} \int \sigma (E) \phi(E) dE (1-e^{- \lambda t}) </math>
 +
 +
For the sage ash, the cross section and the flux are unknown, so reduce this equation to
 +
 +
<math> N_{Sage/Al}(t) = \frac{d_T V_T}{\lambda}(1-e^{- \lambda t}) </math>
 +
 +
where <math> d_T </math> is the density of the target and <math> V_T </math> is the volume of the Al cylinder (assuming the cylinder will be completely filled with sage ash)
 +
 +
<math> V_T = 190.755 cm^3 </math>
 +
 +
 +
For the selenium, we can compute the number of atoms per unit volume, <math> n_T </math>. The mass of a single selenium pellet is approximately 0.1g, while the atomic mass is 78.96u. So the number of atoms in a single selenium pellet is <math> 7.62 \times 10^{20} </math> atoms, which means
 +
 +
<math> n_{Se_T} = 3.812 \times 10^{22} \frac{atoms}{cm^3} </math>
 +
 +
Using the number of atoms vs. the density yields a highly unphysical result. Try using the density for the selenium as well.
 +
 +
<math> d_{Se_T} = 5 \frac{g}{cm^3} </math>
 +
 +
[[File:LB Se SageAsh ProdRate.png|200px]]
 +
 +
The capacitive decline and the differences in half life imply that the production rate will always be higher for the sage ash.
 +
 +
=NAA on Sage/Se Work=
 +
The neutron capture cross sections can be found here https://inis.iaea.org/collection/NCLCollectionStore/_Public/28/060/28060364.pdf
 +
 +
Selenium cross sections begin at page 76.
 +
 +
To recreate the scenario for NAA (44 MeV, 46.34 degrees off of the beam axis), one possible reaction is Se80(N,g)Se81. This is essentially the reverse reaction from the PAA work. Note that Se-80 is more abundant than Se-82 (50% vs. 9%). Unfortunately there still is a chance of producing Se-79 (325000 year half life) through a neutron capture event on Se-78 which is 24% abundant.

Latest revision as of 17:55, 8 November 2018

Mass Information

Note that only 2 samples were produced using the oven method (0.04% and 10%). The target masses are as follows

50% Se/Sage Sample

Selenium Target (50% Sagebrush Se Mix) Mass (g)
Outer Front Ni Foil 0.6948
Se Mass 0.51
Outer Se Mass 0.1
Sagebrush Leaves Mass 0.4969



10% Sample

Selenium Target (10% Sagebrush Se Mix) Mass (g)
Outer Front Ni Foil 0.2783
Se Mass 0.0523
Outer Se Mass 0.0971
Sagebrush Leaves Mass 0.5111


0.1% Se/Sage Sample

Selenium Target (0.1% Sagebrush Se Mix) Mass (g)
Outer Front Ni Foil 1.1437
Se Mass 0.0559
Outer Se Mass 0.1118
Sagebrush Leaves Mass 50.1080



0.04% Sample

Selenium Target (0.04% Sagebrush Se Mix) Mass (g)
Outer Front Ni Foil 0.5447
Se Mass 0.0020
Outer Se Mass 0.0992
Sagebrush Leaves Mass 4.9326


Time Cuts

The first step in the PAA process is to identify the time cuts used for the split run. This must be done for all samples (50%,10%,0.1%, and 0.04%).

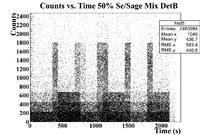
50% Sage/Se Mixture Time Cuts

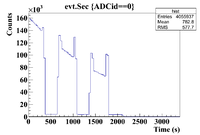
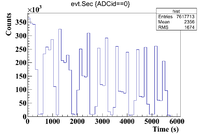
The 50% Se/Sage mixture was measure on Detector B (unshielded, so watch the SNR) on 5/24/17 for a total of 2130.540 seconds. The outer pure witness Se was measure first, and sub-run was roughly 300 seconds for the samples of interest, and 60 seconds for the Co-60 flag. The root command used to draw the timing information was

TTree* tree = MPA;

MPA->Draw("evt.Chan:evt.Sec>>hist2","evt.ADCid == 1");

which produced the histogram below

LB 50 Percent SeSage TimeCutInfo.png

This seems a little sloppy, lets try a 1D histogram instead to see if the cuts are more clear

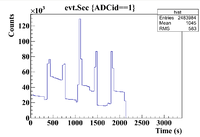
ROOT Command: MPA->Draw("evt.Sec>>hist","ADCid==1","");

This produced the histogram below

LB 50 Percent SeSage TimeCutInfo 1DHistogram.png

This seems much cleaner and clearly shows the time cuts

The time cuts are

0-300 (Pure Se)

375-440 (Co-60)

450-700 (Mixture)

715-780 (Co-60)

800-1010 (Pure Se)

1055-1150 (Co-60)

1160-1420 (Mixture)

1425-1495 (Co-60)

1500-1800 (Pure Se)

1810-1870 (Co-60)

1880-2100 (Mixture)

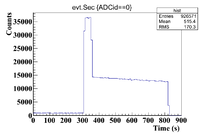
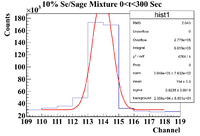
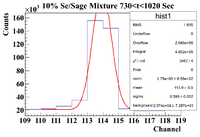
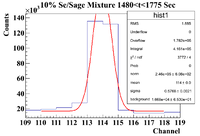
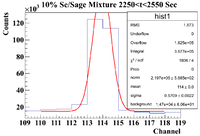
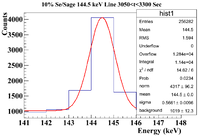
10% Sage/Se Mixture Time Cuts

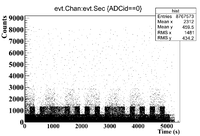
The 10% Se/Sage mixture was measured on Detector A (shielded) on 5/25/17 for a total of 5136.343 seconds. The mixture was measured first, and a sub-run was roughly 300 seconds for the Se samples and 60 seconds for the Co-60 flag. The root commands used were

TTree* tree = MPA;

MPA->Draw("evt.Chan:evt.Sec>>hist2","evt.ADCid == 0");

10Percent SeSage TimingCutInfo.png

10Percent SeSage TimingCutInfo 1DHistogram.png

The time cut information is as follows

0-300 (Mixture)

300-360 (Co-60)

400-640 ( Pure Se)

680-710 (Co-60)

730-1020 (Mixture)

1030-1080 (Co-60)

1100-1360 ( Pure Se)

1400-1440 (Co-60)

1480-1775 (Mixture)

1800-1840 (Co-60)

1875-2150 (Pure Se)

2190-2220 (Co-60)

2250-2550 (Mixture)

2590-2620 (Co-60)

2650-2930 (Pure Se)

2950-3000 (Co-60)

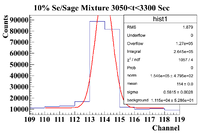
3050-3300 (Mixture)

3390-3350 (Co-60)

3400-3690 (Pure Se)

3700-3750 (Co-60)

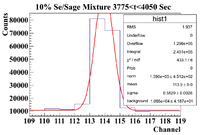
3775-4050 (Mixture)

4060-4100 (Co-60)

4120-4400 (Pure Se)

4420-4470 (Co-60)

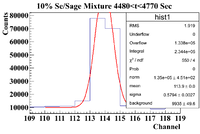
4480-4770 (Mixture)

4790-4820 (Co-60)

4840-5130 (Pure Se)

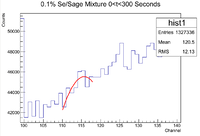
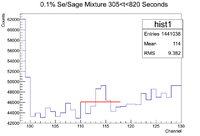
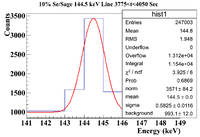
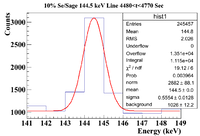
0.1% Sage/Se Mixture Time Cuts

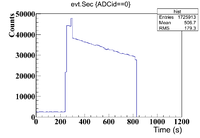
The 0.1% Se/Sage mixture was measured on Detector A (shielded) on 5/24/17 for a total of 2130.540 seconds. The mixture was measured first, and a sub-run was roughly 300 seconds for the Se samples and 60 seconds for the Co-60 flag. The root commands used were

TTree* tree = MPA;

MPA->Draw("evt.Chan:evt.Sec>>hist2","evt.ADCid == 0");

which produced the histogram below

0 1 Percent SeSage TimeCutInfo.png

This seems a little sloppy, so let's repeat the procedure for the 50% sample

ROOT Command:ROOT Command: MPA->Draw("evt.Sec>>hist","ADCid==0","");

This produced the histogram below

0 1 Percent SeSage TimeCutInfo 1DHistogram.png

This is again much better than the 2D histogram.

The time cuts are

0-300 (Mixture)

306-340 (Co-60)

376-640 (Pure Se)

650-720 (Co-60)

730-1010 (Mixture)

1020-1050 (Co-60)

1100-1350 (Pure Se)

1400-1460 (Co-60)

1470-1730 (Mixture)

1735-1800 (Co-60)

1804-2140 (Pure Se)

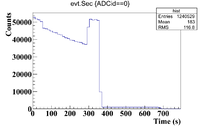
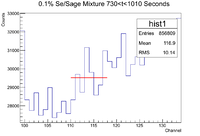
The histogram for the time cuts of the second run is shown below

0 1 Percent SeSage TimeCutInfo 1DHistogram Run2.png

The time cuts are

0-240 (Outer Se)

245-300 (Co-60)

305-820 (Mixture)

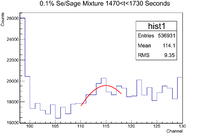
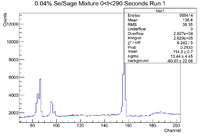
0.04% Sample Time Cuts

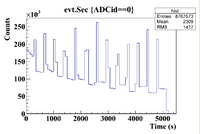
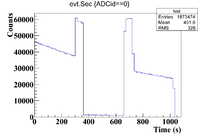
The 0.04% Se/Sage mixture was measured on Detector A (shielded) on 5/25/17 for a total of 1711.891 seconds. The mixture was measured first, and a sub-run was roughly 300 seconds for the Se samples and 60 seconds for the Co-60 flag. The root commands used were

TTree* tree = MPA;

MPA->Draw("evt.Sec>>hist2","evt.ADCid == 0");


The histogram representing the time cuts for the first run are shown below

0 04Percent SeSage TimeCuts 1DHistogram.png

The time cuts for this run are

0-290 (Mixture)

295-360 (Co-60)

370-684 (Pure Se)

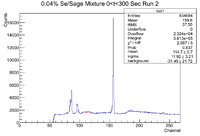
The histogram representing the time cuts for the second run are shown below

0 04Percent SeSage TimeCuts 1DHistogram Run2.png

The time cuts for this run are

0-300 (Mixture)

305-355 (Co-60)

360-650 (Pure Se)

660-735 (Co-60)

740-1020 (Mixture)

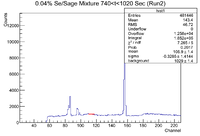
The histogram representing the time cuts for the third run are shown below

It would appear that first two time cuts are difficult to determine because the Co-60 flag's counts are on the same order as the sample's, so watch out for this next time! Each run should be roughly 300 seconds for the sample and 60 seconds for the Co-60 flag, so check the histograms to make sure there are no Co-60 lines to correct for this. To double check these time cuts I looked for Cl-34m in the mixture (which according to my 10% analysis was not present in the pure Se sample) and the Co-60 lines that may have overlapped. It seems there is a line near 1773 keV present in the mixture, but the 1332 keV line is missing in the mixture. Keep an eye out.

0 04Percent SeSage TimeCuts 1DHistogram Run3.png

0-300 (Mixture,145 keV 1173 present | 1332 keV not present,good)

305-350 (Co-60, good)

360-650 (Pure Se, good)

660-710 (Co-60, good)

720-940 (Mixture, good)

1020-1070 (Co-60, good)

1100-1240 (Pure Se, good)

1270-1310 (Co-60, good)

1320-1630 (Mixture, good)

1660-1720 (Co-60, good)

1740-2030 (Pure Se, good)

2040-2120 (Co-60, good)

2130-2420 (Mixture, good)

2430-2490 (Co-60, good)

2500-2800 (Pure Se, good)

2810-2850 (Co-60, good)

2880-3150 (Mixture, good)

3170-3220 (Co-60, good)

3240-3510 (Pure Se, good)

3520-3580 (Co-60, good)

3600-3970 (Mixture, good)

4000-4060 (Co-60, good)

4100-4350 (Pure Se, good)

4370-4420 (Co-60, good)

4450-4710 (Mixture, good)

4730-4780 (Co-60, good)

4800-5080 (Pure Se, good)

5100-5160 (Co-60, good)

5190-5460 (Mixture)

5410-5600 (Co-60)

Below is the histogram representing the time cuts for the 4th run

0 04Percent SeSage TimeCuts 1DHistogram Run4.png

Below are the time cuts

0-300 (Pure Se)

306-359 (Co-60)

362-818 (Mixture)

Gamma Spectrum Analysis

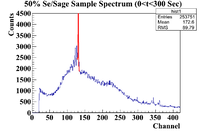
50% Sample Analysis

Below is the analysis table for the 50% Se/Sage mixture. The 103 keV line of Se-81m corresponds to a channel # of 130. Due to the sloppiness of the spectrum, I will use a linear + Gaussian fitting function and restrict my analysis to 6 channels because there are other energy lines nearby. Below is a sample spectrum for an idea of the resolution of Detector B for this measurement

LB 50Percent SeSage SampleSpectrum.png

As a comparison for the constant fit, here is a sample spectrum of the Se/Sage measured by Detector A

10Percent SeSage SampleSpectrum.png


0<t<300
Thin Window Histogram
Signal in Thin Window
Integrated Background
Signal - Background
Runtime (s)
Rate (Hz)
Integral Decay Correction (Hz)
Dead Time (%)
Dead Time Corrected Signal (Hz)
.Dat File Entry For HL Plot

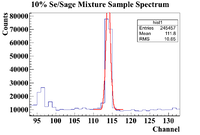
10% Sample Analysis

Below is the analysis table for the 10% Se/Sage mixture. The 103 keV line of Se-81m corresponds to a channel # of 113


0<t<300 730<t<1020 1480<t<1775 2250<t<2550 3050<t<3300 3775<t<4050 4480<t<4770
Thin Window Histogram 10Percent SeSageMix 0 t 300Sec 10Chan Se81m.png 10Percent SeSageMix 730 t 1020Sec 10Chan Se81m.png 10Percent SeSageMix 1480 t 1775Sec 10Chan Se81m.png 10Percent SeSageMix 2250 t 2550Sec 10Chan Se81m.png 10Percent SeSageMix 3050 t 3300Sec 10Chan Se81m.png 10Percent SeSageMix 3775 t 4050Sec 10Chan Se81m.png 10Percent SeSageMix 4480 t 4770Sec 10Chan Se81m.png
Signal in Thin Window [math] 6.019 \times 10^5 \pm 775.82[/math] [math] 4.852 \times 10^5 \pm 696.56 [/math] [math] 4.161 \times 10^5 \pm 645.06 [/math] [math] 3.667 \times 10^5 \pm 605.56 [/math] [math] 2.645 \times 10^5 \pm 514.30 [/math] [math] 2.451 \times 10^5 \pm 495.08 [/math] [math] 2.344 \times 10^5 \pm 484.15 [/math]
Integrated Background [math] 2.956 \times 10^5 \pm 885.1 [/math] [math] 2.074 \times 10^5 \pm 728.7 [/math] [math] 1.668 \times 10^5 \pm 653.0 [/math] [math] 1.47 \times 10^5 \pm 606.0 [/math] [math] 1.115 \times 10^5 \pm 528.6 [/math] [math] 1.055 \times 10^5 \pm 418.7 [/math] [math] 9.935 \times 10^4 \pm 496 [/math]
Signal - Background [math] 3.063 \times 10^5 \pm 1177.01 [/math] [math] 2.778 \times 10^5 \pm 1008.07 [/math] [math] 2.493 \times 10^5 \pm 917.88[/math] [math] 2.197 \times 10^5 \pm 856.70 [/math] [math] 1.53 \times 10^5 \pm 737.51 [/math] [math] 1.396 \times 10^5 \pm 648.39 [/math] [math] 1.35050 \times 10^5 \pm 693.12 [/math]
Runtime (s) 300 290 295 300 250 275 290
Rate (Hz) [math] 1021 \pm 3.92 [/math] [math] 957.93 \pm 3.48 [/math] [math] 845.08 \pm 3.11 [/math] [math] 732.33 \pm 2.86 [/math] [math] 612 \pm 2.95 [/math] [math] 507.64 \pm 2.36 [/math] [math] 465.69 \pm 2.39 [/math]
Integral Decay Correction (Hz) [math] 1052.2 \pm 4.04 [/math] [math] 986.23 \pm 3.58 [/math] [math] 870.47 \pm 3.20 [/math] [math] 754.71 \pm 2.95 [/math] [math] 627.56 \pm 3.03 [/math] [math] 521.85 \pm 2.43 [/math] [math] 479.44 \pm 2.46 [/math]
Dead Time (%) 5.06 +/- 0.39 3.06 +/- 0.30 2.53 +/- 0.31 2.26 +/- 0.33 1.92 +/- 0.26 1.65 +/- 0.34 1.55 +/- 0.18
Dead Time Corrected Signal (Hz)
.Dat File Entry For HL Plot

Background and SNR Information

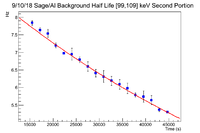
Below is a plot of the background in a 10 channel window around the short lived half life's energy peak of interest (103 keV). The long lived half live can be measured for at least a year even in a 0.1% by mass concentration, so it is less pressing. The values presented are weighted by the mass of the sage ash.

LB 10Percent OvenAshSeMix BackgroundExpoHL.png

The fit parameters are

Constant: 4.50734e+00 +/- 2.42037e-03

Slope: -2.31438e-04 +/- 1.05610e-06

Which gives a rough half life of 49.92 +/- 0.23 minutes

Below is the SNR plotted in xmgrace

LB SNR 10Percent SeSageMix.png

0.1% Sample Analysis

Below is the analysis table for the 0.1% Mixture, the 103 keV line for Se-81m corresponds to a channel # of 113.


0<t<300 730<t<1010 1470<t<1730 305<t<820 (Run 2)
Thin Window Histogram 0 1PercentSeSageMix 0 t 300Sec.png 0 1PercentSeSageMix 730 t 1010Sec.png 0 1PercentSeSageMix 1470 t 1730Sec.png 0 1PercentSeSageMix 305 t 820Sec Run2.png
Signal in Thin Window No Signal Visible No Signal Visible No Signal Visible Possible Signal Visible?
Integrated Background - - - -
Signal - Background - - - -
Runtime (s) 300 280 260 515
Rate (Hz) - - - -
Integral Decay Correction (Hz) - - - -
Dead Time (%) - - - -
Dead Time Corrected Signal (Hz) - - - -
.Dat File Entry For HL Plot - - - -

0.04% Sample Analysis

0<t<290 0<t<300 (Run 2) 740<t<1020 (Run 2)
Thin Window Histogram 0 04Percent SeSage Mix 0 t 290Sec Run1.png 0 04Percent SeSage Mix 0 t 300Sec Run2.png 0 04Percent SeSage Mix 740 t 1020Sec Run2.png
Signal in Thin Window No Signal Visible No Signal Visible No Signal Visible
Integrated Background - - - -
Signal - Background - - - -
Runtime (s) 290 300 280
Rate (Hz) - - - -
Integral Decay Correction (Hz) - - - -
Dead Time (%) - - - -
Dead Time Corrected Signal (Hz) - - - -
.Dat File Entry For HL Plot - - - -

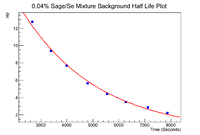
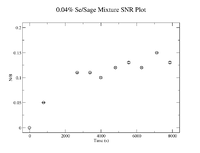
Background and SNR Information

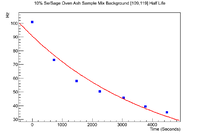
Below is the information for the background in the window [109,119] (Channel # here). The data was weighted by both the runtime and the mass of the sage ash.

0 04Percent SageSeMixture BackgroundHL.png

The fit parameters here are

Constant: 3.42624e+00 +/- 3.71043e-03

Slope: -3.44115e-04 +/- 7.67333e-07

which gives a half life of 33.57 +/- 0.07 minutes.

The SNR plot is shown below

LB 0 04Percent SNRPlot xmgrace.png

Fall 2018 Possible Sage Irradiation Activity Prediction

Isotope Search link: http://nucleardata.nuclear.lu.se/toi/

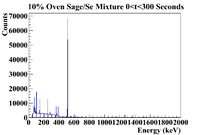
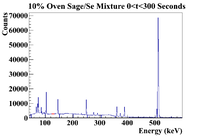
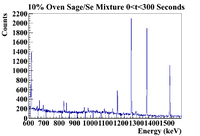
For this section I will attempt to identify the most active line within a sagebrush sample. The histograms that follow in this section will be weighted by the mass of the sage that was used for the sample. I will use the 10% Sage/Se mixture because it was processed using the oven method for dehydration. The mass was 0.5111g which gives a weighting factor of 1.9566 [math] g^{-1} [/math] Below is a full spectrum for the time cut of 0 <t< 300 seconds.

10Percent SeSageMix 0 t 300Sec FullSpectrum PreIrrAnalysis.png

10Percent SeSageMix 0 t 300Sec 0 E 600 PreIrrAnalysis.png 10Percent SeSageMix 0 t 300Sec 600 E 1500 PreIrrAnalysis.png

It seems the two most prominent lines are around 150 keV and 250 keV, so let's try to study the decay of those first.

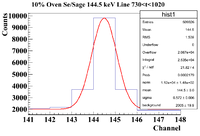
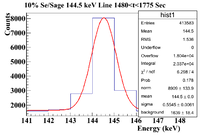
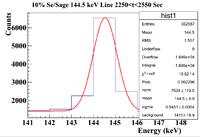
144.5 keV Line

Note: the x-axis for the first 2 histograms should be Energy (keV). This line is NOT present in the Pure Se Sample, so it should be a line produced by the sage itself.

0<t<300 730<t<1020 1480<t<1775 2250<t<2550 3050<t<3300 3775<t<4050 4480<t<4770
Histogram 10Percent SeSageMix 0 t 300Sec 144keVLine PreIrrAnalysis.png 10Percent SeSageMix 730 t 1020Sec 144keVLine PreIrrAnalysis.png 10Percent SeSageMix 1480 t 1775Sec 144keVLine PreIrrAnalysis.png 10Percent SeSageMix 2250 t 2550Sec 144keVLine PreIrrAnalysis.png 10Percent SeSageMix 3050 t 3300Sec 144keVLine PreIrrAnalysis.png 10Percent SeSageMix 3775 t 4050Sec 144keVLine PreIrrAnalysis.png 10Percent SeSageMix 4480 t 4770Sec 144keVLine PreIrrAnalysis.png
Signal in Thin Window 3.424 [math] \times 10^4 \pm [/math] 185.04 2.535 [math] \times 10^4 \pm [/math] 159.22 2.037 [math] \times 10^4 \pm [/math] 142.72 1.695 [math] \times 10^4 \pm [/math] 130.19 1.14 [math] \times 10^4 \pm [/math] 106.77 1.154 [math] \times 10^4 \pm [/math] 107.42 1.115 [math] \times 10^4 \pm [/math] 105.59
Integrated Background 1.9628 [math] \times 10^4 \pm [/math] 167.4 1.4035 [math] \times 10^4 \pm [/math] 139.3 1.1473 [math] \times 10^4 \pm [/math] 128.80 9877 [math] \pm [/math] 118.3 7133 [math] \pm [/math] 86.1 6951.7 [math] \pm [/math] 84.0 7182 [math] \pm [/math] 85.4
Signal - Background 1.4612 [math] \times 10^4 \pm [/math] 249.52 1.1315 [math] \times 10^4 \pm [/math] 211.55 8897 [math] \pm [/math] 192.24 7073 [math] \pm [/math] 175.91 4267 [math] \pm [/math] 137.16 4588.3 [math] \pm [/math] 136.36 3968 [math] \pm [/math] 135.80
Runtime (s) 300 290 295 300 250 275 290
Rate (Hz) 48.71 [math]\pm[/math] 0.83 39.02 [math] \pm [/math] 0.73 30.16 [math] \pm [/math] 0.65 23.58 [math] \pm [/math] 0.59 17.07 [math] \pm [/math] 0.55 16.68 [math] \pm [/math] 0.49 13.68 [math] \pm [/math] 0.47

Without any corrections, the half life here is 38.61 [math] \pm [/math] 0.84 minutes. This is likely Cl-34m (32 min half life) produced by a (g,n) reaction on Cl-35 (75.76% natural abundance), which is stable, because a second line characteristic of Cl-34m was found (1176 keV). This could also be produced by a (g,pn) knockout on Ar-36 in air. This is chlorine since using the isotope search with an energy uncertainty of 5 keV and a half life uncertainty of 10 minutes, the only isotope that shared 146 and 1176 keV with branching ratios that made sense was Cl-34m.


9/10/18 Irradiation

The mass information is

Al Cylinder: 26.0249g

Sage Ash (oven method): 2.0913g

Beam off: 18:30

Calibration

Below is the runlist used for the calibration on Detector D


Source Serial No. Reference Date Activiy Half life Expected Energies (keV) Line Seen (Channel No.) Runtime (s) Position File Name Date Measured
Mn-54 J4-348 8/1/12 9.882 uCi 312.20 days 834.827 835.117 300.601 10 LB_Mn_54_9_10_18_Pos10_DetD 9/10/18
Cs-137 129793 7/1/08 1.066 uCi 30.08 years 661.657 661.887 141.356 10 LB_Cs137_9_10_18_Pos010_DetD 9/10/18
Co-60 129739 07/01/08 1.082 uCi 1925.28 days 1173.228, 1332.492 1173.338, 1332.564 232.521 10 LB_Co60_9_10_18_Pos010_DetD 9/10/18
Ba-133 129790 07/01/08 1.188 uCi 10.551 years 80.9979, 276.3989, 302.8508, 356.0129, 383.8485 81.391, 276.741, 303.166, 356.315, 384.137 250.816 10 LB_Ba133_9_10_18_Pos010_DetD 9/10/18

The calibration coefficients are (according to my fits)

Intercept = -0.370972 +/- 0.616

Slope = 0.490352 +/- 0.000534241

The calibration used at the IAC was

Intercept = 0.272366

Slope = 0.490198

Efficiency

Below is a table of the runlist used for the efficiency on Detector D.

Source Serial No. Reference Date Activiy Half life Expected Energies (keV) Start Stop Runtime (s) Position File Name Date Measured
Mn-54 J4-348 8/1/12 9.882 uCi 312.20 days 828.859 12:45 12:50 300.601 10 LB_Mn_54_9_10_18_Pos10_DetD 9/10/18
Mn-54 J4-348 8/1/12 9.882 uCi 312.20 days 828.859 12:52 12:57 305.787 20 LB_Mn_54_9_10_Pos020_DetD 9/10/18
Mn-54 J4-348 8/1/12 9.882 uCi 312.20 days 828.859 12:59:41 113:04 300.734 30 LB_Mn_54_9_10_18_Pos030_DetD 9/10/18
Co-60 129740 07/01/08 10.42 uCi 1925.28 days 1173.228, 1332.492 18:17:35 18:24 409.011 80 LB_Co60_9_10_18_Pos080_DetD 9/10/18
Co-60 129740 07/01/08 10.42 uCi 1925.28 days 1173.228, 1332.492 18:26:11 18:29 201.084 70 LB_Co60_9_10_18_Pos070_DetD 9/10/18

Runlist for 9/10/18 Irradiated Samples

Sample Date Start Stop Runtime (s) Position Detector % Dead File Name
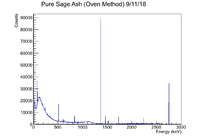
Sage Ash 9/10/18 20:31:35 09:26 46507.875 40 Detector D < 2% LB_SageAsh_OvenMethod_9_10_18_DetD_002
Sage Ash 9/11/18 14:59:50 10:57 71854.534 40 Detector D <1% LB_SageAsh_OvenMethod_9_11_18_DetD_003
Sage Ash 9/12/18 11:01:05 89908.033 20 Detector D <1% LB_SageAsh_OvenMethod_9_12_18_DetD_Pos20_001
Sage Ash 9/13/18 12:03:02 73275.295 10 Det D <1% LB_SageAsh_OvenMethod_9_13_18_DetD_Pos10_001
Sage Ash 9/14/18 09:26:37 10:41 (9/17/18) 10 Det D <1% LB_SageAsh_OvenMethod_9_14_18_DetD_Pos10_001
Sage Ash 9/17/18 10:51:02 10 Det D <1% LB_SageAsh_OvenMethod_9_17_18_DetD_Pos10_001
Sage Ash 10/01/18 14:04:00 Face of Detector Det D <1% LB_SageAsh_OvenMethod_10_1_18_DetD_DetFace_002

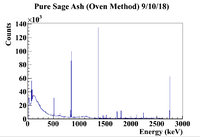
September Sage+Al Analysis

https://wiki.iac.isu.edu/index.php/MCNP_Sim_of_Jack_Converter

Below is the first measured histogram generated from the file LB_SageAsh_OvenMethod_9_10_18_DetD_002. Note that the Al cylinder and the sage ash were not separated, so there will be some lines from Al present. The histogram shown below is not weighted because there are two different samples in front of the detector at the same time (Al cylinder and sage ash). Once the lines have been identified, the mass will be taken into account

The command lines used in the directory /data/IAC/LB_Thesis_Analysis/Sept2018_SageAshBackground/Samples

.L Eff.C

Eff t

t.Loop(RangeMin,RangeMax);


LB SageAshOven 9 10 18 FirstMeasure.png


Below is a histogram of the second measurement taken overnight on 9/11/18

LB SageAshOven 9 11 18 SecondMeasure.png

Now let's overlay these two histograms as a function of activity rather than counts to see if there are any lines that have decayed away that could possibly be identified. I did this as Hz vs. 0.5*(Chan)-0.4. The dithering proved to be quite difficult for both histograms.

LB SageAshOven Measure1and2 Overlay.png

Below is a table detailing the decaying/decayed lines. The relative rates were calculated using a linear fit plus a Gaussian fit, then the background subtracted activity was found.


Line Seen (keV) Isotope
846 Mn-56
1810 Mn-56
2133 Mn-56
1368 Na-24
2754 Na-24

Background Analysis

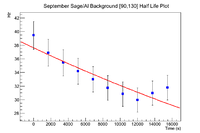
Below is the analysis of the background around the Se line of interest. The histograms were unweighted due to the presence of both the Al cylinder and the sage ash. The data points on the half life plot are weighted by the runtime. The energy window used was [90,130]. The times I concerned myself with spanned 5 half lives of Se (17184 sec) which were split cut into 10 different sets (runtime = 1718.4 sec).

The parameters are as follows


0<t<1718.4 s 1718.4<t<3436.8 s 3436.8<t<5155.2 s 5155.2<t<6873.6 s 6873.6<t<8592 s 8592<t<10310.4 s 10310.4<t<12028.8 s 12028.8<t<13747.2 s 13747.2<t<15461.6 s 15461.6<t<17180 s
Slope ([math] \alpha [/math]) 5.853 [math] \pm [/math] 0.562 5.33 [math] \pm [/math] 0.54 4.981 [math] \pm [/math] 0.532 5.423 [math] \pm [/math] 0.521 6.234 [math] \pm [/math] 0.511 5.155 [math] \pm [/math] 0.503 4.703 [math] \pm [/math] 0.496 4.053 [math] \pm [/math] 0.489 4.49 [math] \pm [/math] 0.49 4.506 [math] \pm [/math] 0.503
Intercept ([math] \beta [/math] ) 1051 [math] \pm [/math] 61.9 998.8 [math] \pm [/math] 59.6 974.6 [math] \pm [/math] 58.7 871.7 [math] \pm [/math] 57.4 731.4 [math] \pm [/math] 56.2 796.7 [math] \pm [/math] 55.4 807.3 [math] \pm [/math] 54.6 841 [math] \pm [/math] 53.9 836.8 [math] \pm [/math] 54.5 868.6 [math] \pm [/math] 55.4
Integral from [90,130] 39.45 [math] \pm [/math] 2.04 36.90 [math] \pm [/math] 1.96 35.44 [math] \pm [/math] 1.92 34.18 [math] \pm [/math] 1.89 32.99 [math] \pm [/math] 1.85 31.74 [math] \pm [/math] 1.82 30.83 [math] \pm [/math] 1.80 29.95 [math] \pm [/math] 1.77 30.98 [math] \pm [/math] 1.78 31.76 [math] \pm [/math] 1.82


Now the total background was found by integrating the linear fit function across the region of interest, in other words

[math] f(x) = \int_a^b (\alpha x + \beta)dx [/math]

To find the error in the integral, use the standard error propagation method

[math] \sigma_f = \sqrt{(\frac{\partial f}{\partial \alpha})^2 \sigma_{\alpha}^2 + (\frac{\partial f}{\partial \beta})^2 \sigma_{\beta}^2} [/math]

[math] = \sqrt{[\frac{\partial}{\partial \alpha}(\int_a^b (\alpha x + \beta)dx)]^2 \sigma_{\alpha}^2 + [\frac{\partial}{\partial \beta}(\int_a^b (\alpha x + \beta)dx)]^2 \sigma_{\beta}^2} [/math]

Since the partial derivatives are not taken with respect to the variable of integration and the function is analytic within the region, the derivative may be moved inside the integral. This action yields

[math]\sigma_f = \sqrt{(\int_a^b x dx)^2 \sigma_{\alpha}^2 + (\int_a^b dx)^2 \sigma_{\beta}^2} [/math]

[math] = \sqrt{(\frac{b^2-a^2}{2})^2 \sigma_{\alpha}^2 + (b-a)^2 \sigma_{\beta}^2} [/math]


Below is the initial plot of the background in the region from [90,130]

LB Sept2018 Sage Al BackgroundHL InitialPlot.png

This plot has some outliers and fluctuations in the background that could be due to the presence of other sources (Dr. Dale was measuring very hot gallium on Det A during my overnight measurement).

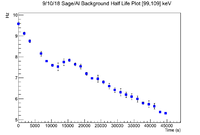
10 Channel Analysis

The fits were done in a larger window [90,130] to get enough bins for a good fit, so I should be able to simply change the bounds of the integration to make the correction. There is definitely some randomness within the time cuts which produce bins with data above and below the fit line, which makes this more difficult. With the dithering, the peak on Detector A has a mean value of 103.949 kev, so the window I will analyze on Detector D (calibrated to energy) will be [99,109] keV


0<t<1718.4 s 1718.4<t<3436.8 s 3436.8<t<5155.2 s 5155.2<t<6873.6 s 6873.6<t<8592 s 8592<t<10310.4 s 10310.4<t<12028.8 s 12028.8<t<13747.2 s 13747.2<t<15461.6 s 15461.6<t<17184 s 17184 <t< 18902.4 s 18902.4 <t< 20620.8 s 20620.8<t<22339.2 s 22339.2<t<24057.6 s 24057.6<t<25776 s 25776<t<27494.4 s 27494.4<t<29212.8 s 29212.8 <t< 30931.2 s 30931.2 <t< 32649.6 s 32649.6<t<34368 s 34368<t<36086.4 s 36086.4<t<37804.8 37804.8 <t< 39523.2 39523.2<t<41241.6 s 41241.6 <t< 42960 s 42960<t<44678.4 s 44678.4 <t< 46396.8 s
Slope ([math] \alpha [/math]) 5.853 [math] \pm [/math] 0.562 5.33 [math] \pm [/math] 0.54 4.981 [math] \pm [/math] 0.532 5.423 [math] \pm [/math] 0.521 6.234 [math] \pm [/math] 0.511 5.155 [math] \pm [/math] 0.503 4.703 [math] \pm [/math] 0.496 4.053 [math] \pm [/math] 0.489 4.49 [math] \pm [/math] 0.49 4.506 [math] \pm [/math] 0.503 5.101 [math] \pm [/math] 0.496 5.215 [math] \pm [/math] 0.490 4.695 [math] \pm [/math] 0.482 4.685 [math] \pm [/math] 0.477 4.731 [math] \pm [/math] 0.468 4.218 [math] \pm [/math] 0.468 3.95 [math] \pm [/math] 0.459 4.388 [math] \pm [/math] 0.452 4.180 [math] \pm [/math] 0.446 3.512 [math] \pm [/math] 0.442 4.423 [math] \pm [/math] 0.440 4.751 [math] \pm [/math] 0.435 3.695 [math] \pm [/math] 0.431 3.372 [math] \pm [/math] 0.424 3.112 [math] \pm [/math] 0.420 3.784 [math] \pm [/math] 0.415 2.792 [math] \pm [/math] 0.414
Intercept ([math] \beta [/math] ) 1051 [math] \pm [/math] 61.9 998.8 [math] \pm [/math] 59.6 974.6 [math] \pm [/math] 58.7 871.7 [math] \pm [/math] 57.4 731.4 [math] \pm [/math] 56.2 796.7 [math] \pm [/math] 55.4 807.3 [math] \pm [/math] 54.6 841 [math] \pm [/math] 53.9 836.8 [math] \pm [/math] 54.5 868.6 [math] \pm [/math] 55.4 769.5 [math] \pm [/math] 54.6 732.8 [math] \pm [/math] 54.0 737.5 [math] \pm [/math] 53.1 715.1 [math] \pm [/math] 52.6 673.8 [math] \pm [/math] 51.6 714.3 [math] \pm [/math] 51.5 701.0 [math] \pm [/math] 50.6 625.5 [math] \pm [/math] 49.8 620.9 [math] \pm [/math] 49.1 676.1 [math] \pm [/math] 48.8 562.8 [math] \pm [/math] 48.4 508.3 [math] \pm [/math] 47.9 600.2 [math] \pm [/math] 47.5 608 [math] \pm [/math] 46.7 623 [math] \pm [/math] 46.3 519.5 [math] \pm [/math] 45.7 618.1 [math] \pm [/math] 45.6
Fit Function Integral from [99,109] 9.67 [math] \pm [/math] 0.50 9.04 [math] \pm [/math] 0.48 8.69 [math] \pm [/math] 0.47 8.35 [math] \pm [/math] 0.46 8.03 [math] \pm [/math] 0.45 7.76 [math] \pm [/math] 0.44 7.54 [math] \pm [/math] 0.44 7.35 [math] \pm [/math] 0.43 7.59 [math] \pm [/math] 0.43 7.78 [math] \pm [/math] 0.44 7.57 [math] \pm [/math] 0.44 7.42 [math] \pm [/math] 0.43 7.13 [math] \pm [/math] 0.42 7.00 [math] \pm [/math] 0.42 6.78 [math] \pm [/math] 0.41 6.71 [math] \pm [/math] 0.41 6.47 [math] \pm [/math] 0.40 6.30 [math] \pm [/math] 0.40 6.14 [math] \pm [/math] 0.39 6.06 [math] \pm [/math] 0.39 5.95 [math] \pm [/math] 0.39 5.83 [math] \pm [/math] 0.38 5.73 [math] \pm [/math] 0.38 5.58 [math] \pm [/math] 0.37 5.51 [math] \pm [/math] 0.37 5.31 [math] \pm [/math] 0.37 5.29 [math] \pm [/math] 0.36
Stats Box Integral [math] 1.674 \times 10^4 [/math] [math] 1.565 \times 10^4 [/math] [math] 1.505 \times 10^4 [/math] [math] 1.159 \times 10^4 [/math] [math] 1.401 \times 10^4 [/math] [math] 1.341 \times 10^4 [/math] [math] 1.306 \times 10^4 [/math] [math] 1.292 \times 10^4 [/math] [math] 1.332 \times 10^4 [/math] [math] 1.347 \times 10^4 [/math] [math] 1.313 \times 10^4 [/math] [math] 1.296 \times 10^4 [/math] [math] 1.238 \times 10^4 [/math] [math] 1.197 \times 10^4 [/math] [math] 1.194 \times 10^4 [/math] [math] 1.166 \times 10^4 [/math] [math] 1.134 \times 10^4 [/math] [math] 1.101 \times 10^4 [/math] [math] 1.085 \times 10^4 [/math] [math] 1.064 \times 10^4 [/math] [math] 1.046 \times 10^4 [/math] [math] 1.027 \times 10^4 [/math] 9943 9872 9699 9206 9110
Stats Box Activity (Hz) 9.58 [math] \pm [/math] 0.07 9.12 [math] \pm [/math] 0.07 8.76 [math] \pm [/math] 0.07 6.74 [math] \pm [/math] 0.06 8.15 [math] \pm [/math] 0.07 7.80 [math] \pm [/math] 0.07 7.60 [math] \pm [/math] 0.07 7.53 [math] \pm [/math] 0.07 7.75 [math] \pm [/math] 0.07 7.84 [math] \pm [/math] 0.07 7.64 [math] \pm [/math] 0.07 7.54 [math] \pm [/math] 0.07 7.20 [math] \pm [/math] 0.06 6.97 [math] \pm [/math] 0.06 6.95 [math] \pm [/math] 0.06 6.79 [math] \pm [/math] 0.06 6.60 [math] \pm [/math] 0.06 6.41 [math] \pm [/math] 0.06 6.31 [math] \pm [/math] 0.06 6.19 [math] \pm [/math] 0.06 6.09 [math] \pm [/math] 0.06 5.98 [math] \pm [/math] 0.06 5.79 [math] \pm [/math] 0.06 5.74 [math] \pm [/math] 0.06 5.64 [math] \pm [/math] 0.06 5.36 [math] \pm [/math] 0.06 5.30 [math] \pm [/math] 0.06
Corrected Background Measurement 9.58 [math] \pm [/math] 0.09 9.12 [math] \pm [/math] 0.08 8.76 [math] \pm [/math] 0.07 6.74 [math] \pm [/math] 1.61 8.15 [math] \pm [/math] 0.12 7.80 [math] \pm [/math] 0.04 7.60 [math] \pm [/math] 0.06 7.53 [math] \pm [/math] 0.18 7.75 [math] \pm [/math] 0.16 7.84 [math] \pm [/math] 0.06 7.64 [math] \pm [/math] 0.07 7.54 [math] \pm [/math] 0.12 7.20 [math] \pm [/math] 0.07 6.97 [math] \pm [/math] 0.03 6.95 [math] \pm [/math] 0.17 6.79 [math] \pm [/math] 0.08 6.60 [math] \pm [/math] 0.13 6.41 [math] \pm [/math] 6.31 [math] \pm [/math] 0.17 6.19 [math] \pm [/math] 0.13 6.09 [math] \pm [/math] 0.14 5.98 [math] \pm [/math] 0.15 5.79 [math] \pm [/math] 0.06 5.74 [math] \pm [/math] 0.16 5.64 [math] \pm [/math] 0.13 5.36 [math] \pm [/math] 0.05 5.30 [math] \pm [/math] 0.01


LB Sept2018 Sage Al BackgroundHL InitialPlot 10Chan Full.png

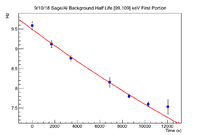
This looks like there are two separate half lives present, so split them up and fit.

LB Sept2018 Sage Al BackgroundHL InitialPlot 10Chan FirstPortion.png

The fit parameters for the first portion are

Slope: -2.22732e-05 +/- 8.61118e-07

Constant:2.25058e+00 +/- 6.19036e-03

Which gives a half life of 8.47 +/- 0.32 hours

LB Sept2018 Sage Al BackgroundHL InitialPlot 10Chan SecondPortion.png

The fit parameters for the second portion are

Constant: 2.24079e+00 +/- 5.78712e-03

Slope: -1.28411e-05 +/- 1.46816e-07

Which gives a half life of 14.99 +/- 0.17 hours

846 keV Line Analysis

Below is the analysis table. The energy window under study is [841,851]


0<t<7751.3125 7751.3125 <t< 15502.625 15502.325 <t< 23253.9375 23253.9375 <t< 31005.25 31005.25 <t< 38756.5625 38756.5625 <t< 46507.875
Histogram PureSageAsh 1stMeasurement 0 t 7751Sec 846keVLine.png PureSageAsh 1stMeasurement 7751 t 15502Sec 846keVLine.png PureSageAsh 1stMeasurement 15502 t 23253Sec 846keVLine.png PureSageAsh 1stMeasurement 23253 t 31005Sec 846keVLine.png PureSageAsh 1stMeasurement 31005 t 38756Sec 846keVLine.png PureSageAsh 1stMeasurement 38756 t 46507Sec 846keVLine.png
Signal in Window 1.013 [math] \times 10^5 \pm [/math] 318.28 5.856 [math] \times 10^4 \pm [/math] 241.99 3.427 [math] \times 10^4 \pm [/math] 185.12 2.062 [math] \times 10^4 \pm [/math] 143.60 1.289 [math] \times 10^4 \pm [/math] 113.53 8254 [math] \pm [/math] 90.85
Integrated Background 6040 [math] \pm [/math] 110 4912 [math] \pm [/math] 98 4295 [math] \pm [/math] 91 3739 [math] \pm [/math] 83 3224 [math] \pm [/math] 77 2889 [math] \pm [/math] 72
Signal - Background 9.5260 [math] \times 10 ^4 \pm [/math] 336.75 5.3648 [math] \times 10^4 \pm [/math] 261.08 2.9975 [math] \times 10^4 \pm [/math] 206.28 1.6881 [math] \times 10^4 \pm [/math] 165.86 9666 [math] \pm [/math] 137.18 5365 [math] \pm [/math] 115.92
Runtime (s) 7751.3125 7751.3125 7751.3125 7751.3125 7751.3125 7751.3125
Rate (Hz) 12.29 [math] \pm [/math] 0.04 6.92 [math] \pm [/math] 0.03 3.87 [math] \pm [/math] 0.03 2.18 [math] \pm [/math] 0.02 1.25 [math] \pm [/math] 0.02 0.69 [math] \pm [/math] 0.01

The exponential decay plot is shown below

PureSageAsh 1stMeasurement 846keVHL ExpoPlot.png


The fit parameters are

Constant: 2.50880 [math] \pm [/math] 0.00287747

Slope: -7.42478 [math] \pm [/math] 0.0249932 [math] \times 10^{-5} [/math]

Which yields a half life of 2.59 [math] \pm [/math] 0.01 hours, which is within one standard deviation of Mn-56's half life (2.58 hours)

The lines that are characteristic with the highest branching ratios of Mn-56 (1810,2133 keV) are both present in the spectrum. This would lead me to believe it is indeed Mn-56 which is produced by either a proton knockout of Fe-57, or neutron capture on Mn-55.

There is also an 834 keV line present, but due to the long half life of Mn-54, this will take some time to analyze, but remember it is there!

1367.5 keV Line Analysis

There is a line decaying at 1367.5 keV. Let's do an analysis on it to see if the isotope can be identified. The window of analysis is [1362,1372]


0<t<7751.32 s 7751.32<t<15502.64 s 15502.64<t<23253.96 s 23253.96<t<31005.28 s 31005.28<t<38756.6 s 38756.6<t<46507.9 s
Histogram LB SageAl 1368keV 0 t 7751 9 10 18.png LB SageAl 1368keV 7751 t 15502 9 10 18.png LB SageAl 1368keV 15502 t 23253 9 10 18.png LB SageAl 1368keV 23253 t 31005 9 10 18.png LB SageAl 1368keV 31005 t 38756 9 10 18.png LB SageAl 1368keV 38756 t 46507 9 10 18.png
Signal in Window [math] 7.472 \times 10^4 [/math] [math] 6.7 \times 10^4 [/math] [math] 6.129 \times 10^4 [/math] [math] 5.567 \times 10^4 [/math] [math] 4.97 \times 10^4 [/math] [math] 4.525 \times 10^4 [/math]
Integrated Background 2732 [math] \pm [/math] 44 2145 [math] \pm [/math] 39 1746 [math] \pm [/math] 35 1552 [math] \pm [/math] 33 1312 [math] \pm [/math] 30 1188 [math] \pm [/math] 29
Signal - Background 71988 [math] \pm [/math] 276.868 64855 [math] \pm [/math] 261.765 59544 [math] \pm [/math] 250.03 54118 [math] \pm [/math] 238.241 48388 [math] \pm [/math] 224.944 44062 [math] \pm [/math] 214.688
Runtime (s) 7751.32 7751.32 7751.32 7751.32 7751.32 7751.3
Rate (Hz) 9.29 [math] \pm [/math] 0.04 8.37 [math] \pm [/math] 0.03 7.68 [math] \pm [/math] 0.03 6.98 [math] \pm [/math] 0.03 6.24 [math] \pm [/math] 0.03 5.68 [math] \pm [/math] 0.03

LB SageAL 1368keV HalfLifePlot.png

The fit parameters are

constant: 2.22835e+00 +/- 2.95795e-03

slope: -1.26126e-05 +/- 1.41004e-07

which gives a half life of 15.26 +/- 0.17 hours. This is within 2 standard deviations of Na-24's half life. This isotope also has a line present at 2754 keV, which is present in the energy spectrum. Also this is the only isotope with branching ratios compatible with the gamma spectrum data. This would be a neutron capture on stable Na-23.

2242 keV Analysis

There is a decaying line seen at 2242 keV. The analysis was done in a 16 channel window from [2234,2250]

0<t<3875.66 s 3875.66<t<7751.32 s 7751.32<t<11626.98 s 11626.98<t<15502.64 s 15502.64<t<19378.3 s 19378.3<t<23253.96 s 23253.96<t<27129.62 s 27129.62<t<31005.28 s 31005.28<t<34880.94 s 34880.94<t<38756.6 s 38756.6<t<42632.26 s 42632.26<t<46507.9 s
Histogram LB SageAl 2242keVLine 0 t 3875.66 9 10 18.png LB SageAl 2242keVLine 3875.66 t 7751.32 9 10 18.png LB SageAl 2242keVLine 7751 t 11626 9 10 18.png LB SageAl 2242keVLine 11626 t 15502 9 10 18.png LB SageAl 2242keVLine 15502 t 19378 9 10 18.png LB SageAl 2242keVLine 19378 t 23253 9 10 18.png LB SageAl 2242keVLine 23253 t 27129 9 10 18.png LB SageAl 2242keVLine 27129 t 31005 9 10 18.png LB SageAl 2242keVLine 31005 t 34880 9 10 18.png LB SageAl 2242keVLine 34880 t 38756 9 10 18.png LB SageAl 2242keVLine 38756 t 42632 9 10 18.png LB SageAl 2242keVLine 42632 t 46507 9 10 18.png
Signal in Window 4792 4625 4355 4124 3975 3759 3498 3479 3280 3041 2945 2807
Integrated Background 1686.4 [math] \pm [/math] 35.2 1567.36 [math] \pm [/math] 33.76 1418.56 [math] \pm [/math] 32.32 1355.68 [math] \pm [/math] 31.52 1347.52 [math] \pm [/math] 31.2 1300 [math] \pm [/math] 30.72 1152.48 [math] \pm [/math] 29.12 1198.24 [math] \pm [/math] 29.44 1111.36 [math] \pm [/math] 28.48 1012.48 [math] \pm [/math] 27.36 969.6 [math] \pm [/math] 27.2 925.76 [math] \pm [/math] 26.08
Signal - Background 3105.6 [math] \pm [/math] 77.66 3057.64 [math] \pm [/math] 75.93 2936.44 [math] \pm [/math] 73.48 2768.32 [math] \pm [/math] 71.54 2627.48 [math] \pm [/math] 70.35 2459 [math] \pm [/math] 68.58 2345.52 [math] \pm [/math] 65.92 2280.76 [math] \pm [/math] 65.92 2168.64 [math] \pm [/math] 63.96 2028.52 [math] \pm [/math] 61.56 1975.4 [math] \pm [/math] 60.70 1881.24 [math] \pm [/math] 59.05
Runtime (s) 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.64
Rate (Hz) 0.80 [math] \pm [/math] 0.02 0.79 [math] \pm [/math] 0.02 0.76 [math] \pm [/math] 0.02 0.71 [math] \pm [/math] 0.02 0.68 [math] \pm [/math] 0.02 0.63 [math] \pm [/math] 0.02 0.61 [math] \pm [/math] 0.02 0.59 [math] \pm [/math] 0.02 0.56 [math] \pm [/math] 0.02 0.52 [math] \pm [/math] 0.02 0.51 [math] \pm [/math] 0.02 0.48 [math] \pm [/math] 0.02

LB 2242keVLine HLPlot.png

The fit parameters are

Constant: -1.99924e-01 +/- 1.47295e-02

Slope: -1.24500e-05 +/- 6.90105e-07

1731 keV Analysis

There is a decaying line seen at 1731 keV in the Sage/Al samples from 9/10/18. The analysis was done in a 10 channel window from [1726,1736]

0<t<3875.66 s 3875.66<t<7751.32 s 7751.32<t<11626.98 s 11626.98<t<15502.64 s 15502.64<t<19378.3 s 19378.3<t<23253.96 s 23253.96<t<27129.62 s 27129.62<t<31005.28 s 31005.28<t<34880.94 s 34880.94<t<38756.6 s 38756.6<t<42632.26 s 42632.26<t<46507.9 s
Histogram LB SageAl 1731keV 0 3875s 9 10 18.png
Signal in Window 3799
Integrated Background 1005 +/- 27
Signal - Background
Runtime (s) 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.66 3875.64
Rate (Hz)

Production Optimization

The sage ash has a density of 0.1977 [math] \frac{g}{cm^3} [/math]. To perform this I will use an 8 hour half life from the sage ash/Al sample irradiated on 9/10/18.

8 Hour Half Life (9/10/18)

This section focuses on optimization for the sage/Al cylinder 8 hour half life performed above. The decay constant for that sample was -2.22732e-05 +/- 8.61118e-07 [math] s^{-1} [/math]. The production rate is given by

[math] N(t) = \frac{n_T V_T}{\lambda} \int \sigma (E) \phi(E) dE (1-e^{- \lambda t}) [/math]

For the sage ash, the cross section and the flux are unknown, so reduce this equation to

[math] N_{Sage/Al}(t) = \frac{d_T V_T}{\lambda}(1-e^{- \lambda t}) [/math]

where [math] d_T [/math] is the density of the target and [math] V_T [/math] is the volume of the Al cylinder (assuming the cylinder will be completely filled with sage ash)

[math] V_T = 190.755 cm^3 [/math]


For the selenium, we can compute the number of atoms per unit volume, [math] n_T [/math]. The mass of a single selenium pellet is approximately 0.1g, while the atomic mass is 78.96u. So the number of atoms in a single selenium pellet is [math] 7.62 \times 10^{20} [/math] atoms, which means

[math] n_{Se_T} = 3.812 \times 10^{22} \frac{atoms}{cm^3} [/math]

Using the number of atoms vs. the density yields a highly unphysical result. Try using the density for the selenium as well.

[math] d_{Se_T} = 5 \frac{g}{cm^3} [/math]

LB Se SageAsh ProdRate.png

The capacitive decline and the differences in half life imply that the production rate will always be higher for the sage ash.

NAA on Sage/Se Work

The neutron capture cross sections can be found here https://inis.iaea.org/collection/NCLCollectionStore/_Public/28/060/28060364.pdf

Selenium cross sections begin at page 76.

To recreate the scenario for NAA (44 MeV, 46.34 degrees off of the beam axis), one possible reaction is Se80(N,g)Se81. This is essentially the reverse reaction from the PAA work. Note that Se-80 is more abundant than Se-82 (50% vs. 9%). Unfortunately there still is a chance of producing Se-79 (325000 year half life) through a neutron capture event on Se-78 which is 24% abundant.

Retrieved from "https://wiki.iac.isu.edu/index.php?title=LB_SageBrushWork_PostDefense&oldid=125648"