Difference between revisions of "LB Thesis Theory Section"
| (19 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
==General PAA Method== | ==General PAA Method== | ||
| − | Photon activation analysis (PAA) is a method used to determine the isotopic composition of a sample based on the characteristic photon energies emitted by gamma decays of radioactive isotopes that have been activated by bremsstrahlung photons.. The sample is activated using a Linear Accelerator (LINAC) to accelerate electrons towards an aluminum/tungsten radiator and produce Bremsstrahlung radiation from those electrons that slow down within the radiator. Some of those Bremsstrahlung photons are of sufficient energy to free a nucleon(s) from the target nuclei in the sample of interest. We can estimate the energy required to knock out a neutron from Se-82 with a simple formula (in natural units): | + | Photon activation analysis (PAA) is a method used to determine the isotopic composition of a sample based on the characteristic photon energies emitted by gamma decays of radioactive isotopes that have been activated by bremsstrahlung photons.. The sample is activated using a Linear Accelerator (LINAC) to accelerate electrons towards an aluminum/tungsten radiator and produce Bremsstrahlung radiation from those electrons that slow down within the radiator. Some of those Bremsstrahlung photons are of sufficient energy to free a nucleon(s) from the target nuclei in the sample of interest. |
| + | |||
| + | By running simulations on GEANT4, the energy spectrum of the Bremsstrahlung photons and the angular distribution has been created. | ||
| + | |||
| + | [[Show pics of spectra when pics can be added]] | ||
| + | |||
| + | We can estimate the energy required to knock out a neutron from Se-82 with a simple formula (in natural units): | ||
<math> E_{knockout} -> M_{Se-82} - M_{Se-81} + M_{neutron} </math> | <math> E_{knockout} -> M_{Se-82} - M_{Se-81} + M_{neutron} </math> | ||
| Line 9: | Line 15: | ||
<math> E_{knockout} -> 76304.92 - 75374.63 + 939.57 = 9.3 MeV </math> | <math> E_{knockout} -> 76304.92 - 75374.63 + 939.57 = 9.3 MeV </math> | ||
| − | So the energy of the accelerator used must be greater than 9.3 MeV. Another piece of information that is utilized when deciding which beam energy to use is the cross section for the desired reaction | + | So the energy of the accelerator used must be greater than 9.3 MeV. Another piece of information that is utilized when deciding which beam energy to use is the cross section for the desired reaction. By researching the cross sections and finding which energy will produce the most isotopes of interest, one can attempt to make the sample active enough to see energy lines within the background. |
(here we didn't really use the cross section to determine the energy of the beam since we were not funded. We only really used the cross section to predict the activities of the radioactive isotopes, but even still the data would need to be extrapolated to try and get a more accurate prediction) | (here we didn't really use the cross section to determine the energy of the beam since we were not funded. We only really used the cross section to predict the activities of the radioactive isotopes, but even still the data would need to be extrapolated to try and get a more accurate prediction) | ||
| Line 17: | Line 23: | ||
[[File:170063 EnergySpectrumSample.png|200px]] | [[File:170063 EnergySpectrumSample.png|200px]] | ||
| − | Note that there will be many different isotopic decay lines present in the spectrum, but there are several methods to ensure that information about the isotope of interest can be found. The first step to proving that a specific isotope is present | + | Note that there will be many different isotopic gamma decay lines present in the spectrum, but there are several methods to ensure that information about the isotope of interest can be found. The first step to proving that a specific isotope is present within a sample is to first look at the energy lines. Since each isotope has characteristic gamma decay lines, if the isotope is present, then those lines should be apparent in the spectrum (assuming the branching ratio is high enough that the lines don't get washed out in the background). Consider some isotope of interest that has 3 large characteristic decay lines. If all of those 3 lines are present in the spectrum, then that would be a good indicator that the isotope of interest might possibly be in the sample. Unfortunately more information is needed due to the fact that there are so many isotopes that 3 separate isotopes (or some other combination) could produce spectral lines close to the energy lines of the isotope of interest, which would produce a false positive. To strengthen the argument, multiple measurements can be made using the same sample to see how the rate of the signal decays over time. By finding how the rate of the signal of interest decays with time, one can apply the standard radioactive decay equation to find the half life of the isotope. |
<math> A_{Measured} = A_0 e^{-\lambda t} </math> | <math> A_{Measured} = A_0 e^{-\lambda t} </math> | ||
| Line 25: | Line 31: | ||
[[File:Se81 Metastable 103keV overlay.png|200px]] | [[File:Se81 Metastable 103keV overlay.png|200px]] | ||
| − | It can be seen above that the same energy line will become less apparent as time goes on due to the decay. By measuring the activity at several points in time, a plot of the measured activity as a function of time can be created. By fitting this function (whether linearly | + | It can be seen above that the same energy line will become less apparent as time goes on due to the decay. By measuring the activity at several points in time, a plot of the measured activity as a function of time can be created. By fitting this function (whether linearly or exponentially), the fit parameters will give the initial activity and the decay constant. If the energy lines are present and the half life agrees with the isotope of interest, then the argument strengthens. There is one more step that can be taken to ensure the isotope of interest is present in the sample. Looking at the branching ratios for the different energy lines can provide a stronger argument. Consider some isotope of interest A that has two decay lines with branching ratios of 80% and 40%. By looking at the efficiency corrected rate seen by the detector for these lines, the ratio between the activities measured should be around 2, meaning that the first decay happens roughly twice as often as the second decay. Using all three of these pieces the experimenter can provide a strong argument for the isotope of interest being present in the sample. |
This method of compositional analysis has many applications such as verifying a counterfeit product, and finding concentrations of contaminants in a sample. | This method of compositional analysis has many applications such as verifying a counterfeit product, and finding concentrations of contaminants in a sample. | ||
| Line 33: | Line 39: | ||
| − | There are 3 reactions of interest: | + | There are 3 reactions of interest and their neutron knockout cross sections are shown below: |
| + | |||
| + | [[File:LB SeIsotopeXSect Plot.png|200px]] | ||
==<math> {80 \atop 34\; }Se (\gamma,n){79 \atop 34\;}Se </math>== | ==<math> {80 \atop 34\; }Se (\gamma,n){79 \atop 34\;}Se </math>== | ||
| + | This reaction must be taken into consideration because Se-79 has a half life of <math> 3.27 \times 10^5 </math> years, which makes it difficult to deal with as it is mixed waste. By using nickel normalization, one can predict how much Se-79 will be made. See [[LB PAA Nickel Investigation]] for more information. | ||
| − | ==<math> {82 \atop 34\; }Se (\gamma,n){81 \atop 34\;Se | + | ==<math> {82 \atop 34\; }Se (\gamma,n){81 \atop 34\;}Se </math>== |
| − | This is the reaction that will me most studied in this experiment. It has only 1 line of interest, which is at 103.01 keV with a branching ratio of 12.8%. The half life of the metastable state of Se-81 is 57.28 +/- 0.02 minutes. | + | This is the reaction that will me most studied in this experiment. It has only 1 line of interest, which is at 103.01 keV with a branching ratio of 12.8%. The half life of the metastable state of Se-81 is 57.28 +/- 0.02 minutes. The reason that this reaction is so important is because it is the limiting factor to determine isotopic ratios of interest. With such a short half life and a highly active matrix after being removed from the beam, it must be determined if this reaction can be seen first. The other isotopes of interest have much longer half lives, which allows the matrix to decay and become less active before measuring. Unfortunately here not much can be done about the active matrix, so the measurement of this isotope is key for future investigations to continue. |
| − | ==<math> {76 \atop 34\; }Se (\gamma,n){75 \atop 34\;Se} </math>== | + | ==<math> {76 \atop 34\; }Se (\gamma,n){75 \atop 34\;}Se </math>== |
| + | |||
| + | ==Predicted Activities and Production Rate Theory== | ||
| + | When performing photon activation analysis, it is important to estimate how many activated nuclei will be produced. An equation for the production rate can be written as the number of nucleons activated subtracted by the number of nucleons that decay away during the irradiation process. | ||
| + | |||
| + | |||
| + | <math>\frac{dN(t)}{dt} = N \sigma \phi - \lambda N(t)</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | ;<math>\frac{dN(t)}{dt} = </math>Production Rate of nuclei | ||
| + | ;<math> N = </math> Number of Nuclei | ||
| + | ;<math> \sigma = </math> The cross section for the reaction | ||
| + | ;<math> \phi = </math> The photon flux through the target | ||
| + | ;<math> \lambda = </math> The decay constant of the isotope of interest | ||
| + | |||
| + | which gives a solution of | ||
| + | |||
| + | <math> N(t) = \frac{N \sigma \phi}{\lambda}\left ( 1 - e^{-\lambda t} \right )</math> | ||
| + | |||
| + | *Create plot of capacitive effect? | ||
| − | |||
[[LB PAA Nickel Investigation]] | [[LB PAA Nickel Investigation]] | ||
==Minimum Detectable Activity Calculations== | ==Minimum Detectable Activity Calculations== | ||
Reference: [[LB MDA/Se Mass Calculations]] | Reference: [[LB MDA/Se Mass Calculations]] | ||
| − | |||
| − | |||
| − | |||
==Geometric Efficiency Calculations== | ==Geometric Efficiency Calculations== | ||
Latest revision as of 17:22, 12 March 2018
PAA Theory
General PAA Method
Photon activation analysis (PAA) is a method used to determine the isotopic composition of a sample based on the characteristic photon energies emitted by gamma decays of radioactive isotopes that have been activated by bremsstrahlung photons.. The sample is activated using a Linear Accelerator (LINAC) to accelerate electrons towards an aluminum/tungsten radiator and produce Bremsstrahlung radiation from those electrons that slow down within the radiator. Some of those Bremsstrahlung photons are of sufficient energy to free a nucleon(s) from the target nuclei in the sample of interest.
By running simulations on GEANT4, the energy spectrum of the Bremsstrahlung photons and the angular distribution has been created.
Show pics of spectra when pics can be added
We can estimate the energy required to knock out a neutron from Se-82 with a simple formula (in natural units):
So the energy of the accelerator used must be greater than 9.3 MeV. Another piece of information that is utilized when deciding which beam energy to use is the cross section for the desired reaction. By researching the cross sections and finding which energy will produce the most isotopes of interest, one can attempt to make the sample active enough to see energy lines within the background.
(here we didn't really use the cross section to determine the energy of the beam since we were not funded. We only really used the cross section to predict the activities of the radioactive isotopes, but even still the data would need to be extrapolated to try and get a more accurate prediction)
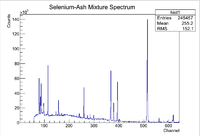
After the nucleons have been liberated from the nucleus, the nucleus becomes unstable and starts to undergo nuclear decay. The nuclear decay can emit photons that have energies characteristic to each isotope enabling the construction of a compositional fingerprint once the detected photon emission rates are also shown to have the half life of the assumed isotope. Typically High Purity Germanium Detectors are used to count the photons and measure the photon energy for the sample of interest. A typical photon energy distribution from an activated sample as measured by the HpGe detector is shown below
Note that there will be many different isotopic gamma decay lines present in the spectrum, but there are several methods to ensure that information about the isotope of interest can be found. The first step to proving that a specific isotope is present within a sample is to first look at the energy lines. Since each isotope has characteristic gamma decay lines, if the isotope is present, then those lines should be apparent in the spectrum (assuming the branching ratio is high enough that the lines don't get washed out in the background). Consider some isotope of interest that has 3 large characteristic decay lines. If all of those 3 lines are present in the spectrum, then that would be a good indicator that the isotope of interest might possibly be in the sample. Unfortunately more information is needed due to the fact that there are so many isotopes that 3 separate isotopes (or some other combination) could produce spectral lines close to the energy lines of the isotope of interest, which would produce a false positive. To strengthen the argument, multiple measurements can be made using the same sample to see how the rate of the signal decays over time. By finding how the rate of the signal of interest decays with time, one can apply the standard radioactive decay equation to find the half life of the isotope.
An example of a decaying energy line can be seen below
It can be seen above that the same energy line will become less apparent as time goes on due to the decay. By measuring the activity at several points in time, a plot of the measured activity as a function of time can be created. By fitting this function (whether linearly or exponentially), the fit parameters will give the initial activity and the decay constant. If the energy lines are present and the half life agrees with the isotope of interest, then the argument strengthens. There is one more step that can be taken to ensure the isotope of interest is present in the sample. Looking at the branching ratios for the different energy lines can provide a stronger argument. Consider some isotope of interest A that has two decay lines with branching ratios of 80% and 40%. By looking at the efficiency corrected rate seen by the detector for these lines, the ratio between the activities measured should be around 2, meaning that the first decay happens roughly twice as often as the second decay. Using all three of these pieces the experimenter can provide a strong argument for the isotope of interest being present in the sample.
This method of compositional analysis has many applications such as verifying a counterfeit product, and finding concentrations of contaminants in a sample.
Neutron Knockout of Selenium
Talk bout the 3 neutron knockouts of interest (81,75,79) and provide the half lives for each isotope. Also here include the cross section plots.
There are 3 reactions of interest and their neutron knockout cross sections are shown below:
This reaction must be taken into consideration because Se-79 has a half life of years, which makes it difficult to deal with as it is mixed waste. By using nickel normalization, one can predict how much Se-79 will be made. See LB PAA Nickel Investigation for more information.
This is the reaction that will me most studied in this experiment. It has only 1 line of interest, which is at 103.01 keV with a branching ratio of 12.8%. The half life of the metastable state of Se-81 is 57.28 +/- 0.02 minutes. The reason that this reaction is so important is because it is the limiting factor to determine isotopic ratios of interest. With such a short half life and a highly active matrix after being removed from the beam, it must be determined if this reaction can be seen first. The other isotopes of interest have much longer half lives, which allows the matrix to decay and become less active before measuring. Unfortunately here not much can be done about the active matrix, so the measurement of this isotope is key for future investigations to continue.
Predicted Activities and Production Rate Theory
When performing photon activation analysis, it is important to estimate how many activated nuclei will be produced. An equation for the production rate can be written as the number of nucleons activated subtracted by the number of nucleons that decay away during the irradiation process.
where
- Production Rate of nuclei
- Number of Nuclei
- The cross section for the reaction
- The photon flux through the target
- The decay constant of the isotope of interest
which gives a solution of
- Create plot of capacitive effect?
Minimum Detectable Activity Calculations
Reference: LB MDA/Se Mass Calculations