Difference between revisions of "Initial CM Frame 4-momentum components"
Jump to navigation
Jump to search
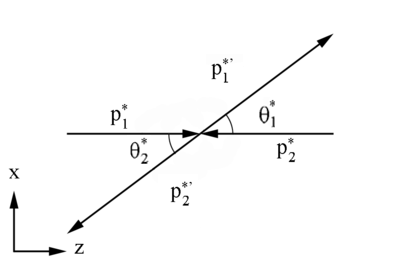
Figure 2: Definition of variables in the Center of Mass Frame
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <center><math>\underline{\textbf{Navigation}}</math> | ||
| + | [[Initial_Lab_Frame_4-momentum_components|<math>\vartriangleleft </math>]] | ||
| + | [[VanWasshenova_Thesis#Initial_4-momentum_Components|<math>\triangle </math>]] | ||
| + | [[Special_Case_of_Equal_Mass_Particles|<math>\vartriangleright </math>]] | ||
| + | |||
| + | </center> | ||
| + | |||
| + | |||
=Initial CM Frame 4-momentum components= | =Initial CM Frame 4-momentum components= | ||
| Line 15: | Line 23: | ||
| − | <center><math>\frac {d\vec p}{dt}=0\Rightarrow \frac{d(m\vec v)}{dt}=\frac{ | + | <center><math>\frac {d\vec p}{dt}=0\Rightarrow \frac{d(m\vec v)}{dt}=\frac{v\ dm}{dt}\Rightarrow \frac{dm}{dt}=0</math></center> |
| Line 46: | Line 54: | ||
<center><math>{\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=(m_1+m_2)^2=s</math></center> | <center><math>{\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=(m_1+m_2)^2=s</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | |||
| + | <center><math>\underline{\textbf{Navigation}}</math> | ||
| + | |||
| + | [[Initial_Lab_Frame_4-momentum_components|<math>\vartriangleleft </math>]] | ||
| + | [[VanWasshenova_Thesis#Initial_4-momentum_Components|<math>\triangle </math>]] | ||
| + | [[Special_Case_of_Equal_Mass_Particles|<math>\vartriangleright </math>]] | ||
| + | |||
| + | </center> | ||
Latest revision as of 18:53, 15 May 2018
Initial CM Frame 4-momentum components

Starting with the definition for the total relativistic energy:
Since we can assume that the frame of reference is an inertial frame, it moves at a constant velocity, the mass should remain constant.
We can use 4-momenta vectors, i.e. ,with c=1, to describe the variables in the CM Frame.
Using the fact that the scalar product of a 4-momenta with itself,
is invariant.
Using this notation, the sum of two 4-momenta forms a 4-vector as well
The length of this four-vector is an invariant as well