Difference between revisions of "Center of Mass for Stationary Target"
Jump to navigation
Jump to search
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<center><math>\textbf{\underline{Navigation}}</math> | <center><math>\textbf{\underline{Navigation}}</math> | ||
| − | [[ | + | [[Uniform_distribution_in_Energy_and_Theta_LUND_files|<math>\vartriangleleft </math>]] |
| − | [[VanWasshenova_Thesis# | + | [[VanWasshenova_Thesis#Weighted_Isotropic_Distribution_in_Lab_Frame|<math>\triangle </math>]] |
| − | [[ | + | [[Phase_space_Limiting_Particles|<math>\vartriangleright </math>]] |
</center> | </center> | ||
| + | |||
| + | =4.1.1 Center of Mass for Stationary Target= | ||
| + | |||
| + | For an [[DV_Calculations_of_4-momentum_components#Center_of_Mass_Frame|incoming electron of 11GeV striking a stationary electron]] we would expect: | ||
| + | |||
| + | |||
| + | Inspecting the Lorentz transformation to the Center of Mass frame: | ||
| + | |||
| + | |||
| + | <center><math>\left( \begin{matrix}E^*_{1}+E^*_{2}\\ 0 \\ 0 \\ 0\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+E_{2}\\ 0 \\ 0 \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)</math></center> | ||
| + | |||
| + | |||
| + | For the case of a stationary electron, this simplifies to: | ||
| + | |||
| + | <center><math>\left( \begin{matrix} E^* \\ p^*_{x} \\ p^*_{y} \\ p^*_{z}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^*\gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+m\\ 0 \\ 0 \\ p_{1(z)}+0\end{matrix} \right)</math></center> | ||
| + | |||
| + | |||
| + | which gives, | ||
| + | |||
| + | |||
| + | <center><math>\Longrightarrow\begin{cases} | ||
| + | E^*=\gamma^* (E_{1}+m)-\beta^* \gamma^* p_{1(z)} \\ | ||
| + | p^*_{z}=-\beta^* \gamma^*(E_{1}+m)+\gamma^* p_{1(z)} | ||
| + | \end{cases}</math></center> | ||
| + | |||
| + | |||
| + | Solving for <math>\beta^*</math>, with <math>p^*_{z}=0</math> | ||
| + | |||
| + | <center><math>\Longrightarrow \beta^* \gamma^*(E_{1}+m)=\gamma^* p_{1(z)}</math></center> | ||
| + | |||
| + | |||
| + | {| class="wikitable" align="center" | ||
| + | | style="background: gray" | <math>\Longrightarrow \beta^*=\frac{p_{1}}{(E_{1}+m)}</math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | Similarly, solving for <math>\gamma^*</math> by substituting in <math>\beta^*</math> | ||
| + | |||
| + | |||
| + | <center><math>E^*=\gamma^* (E_{1}+m)-\frac{p_{1}}{(E_{1}+m)} \gamma^* p_{1(z)}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>E^*=\gamma^* \frac{(E_{1}+m)^2}{(E_{1}+m)}-\gamma^*\frac{(p_{1(z)})^2}{(E_{1}+m)}</math></center> | ||
| + | |||
| + | |||
| + | Using the fact that <math>E^*=[(E_{1}+E_{2})^2-(\vec p_{1}+\vec p_{2})^2]^{1/2}</math> | ||
| + | |||
| + | |||
| + | <center><math>E^*=\gamma^* \frac{E^*\ ^2}{(E_{1}+m)}</math></center> | ||
| + | |||
| + | {| class="wikitable" align="center" | ||
| + | | style="background: gray" | <math>\Longrightarrow \gamma^*=\frac{(E_1+m)} {E^*}</math> | ||
| + | |} | ||
| − | + | ||
| + | Using the relation | ||
| + | |||
| + | <center><math>\left( \begin{matrix} E^*_{1}+E^*_{2} \\ p^*_{1(x)}+p^*_{2(x)} \\ p^*_{1(y)}+p^*_{2(y)} \\ p^*_{1(z)}+p^*_{2(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+m\\ 0 \\ 0 \\ p_{1(z)}+0\end{matrix} \right)</math></center> | ||
| Line 17: | Line 74: | ||
| + | <center><math>\Longrightarrow\begin{cases} | ||
| + | E^*_{2}=\gamma^* (m) \\ | ||
| + | p^*_{2(z)}=-\beta^* \gamma^* (m) | ||
| + | \end{cases}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\Longrightarrow\begin{cases} | ||
| + | E^*_{2}=\frac{(E_{1}+m)}{E^*} (m) \\ | ||
| + | p^*_{2(z)}=-\frac{p_{1}}{(E_{1}+m)} \frac{(E_{1}+m)}{E^*} (m_{2}) | ||
| + | \end{cases}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\Longrightarrow\begin{cases} | ||
| + | E^*_{2}=\frac{(11000 MeV+.511 MeV)}{106.031 MeV} (.511 MeV) \approx 53.015 MeV\\ | ||
| + | p^*_{2(z)}=-\frac{11000 MeV}{106.031 MeV} (.511 MeV) \approx -53.013 MeV | ||
| + | \end{cases}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\Longrightarrow \left( \begin{matrix} E^*_{1}\\ p^*_{1(x)} \\ p^*_{1(y)} \\ p^*_{1(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}\\ 0 \\ 0 \\ p_{1(z)}\end{matrix} \right)</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\Longrightarrow\begin{cases} | ||
| + | E^*_{1}=\gamma^* (E_{1})-\beta^* \gamma^* p_{1(z)} \\ | ||
| + | p^*_{1(z)}=-\beta^* \gamma^*(E_{1})+\gamma^* p_{1(z)} | ||
| + | \end{cases}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\Longrightarrow\begin{cases} | ||
| + | E^*_{1}=\frac{(E_{1}+m)}{E^*} (E_{1})-\frac{p_{1(z)}}{(E_{1}+m)} \frac{(E_{1}+m)}{E^*} p_{1(z)} \\ | ||
| + | p^*_{1(z)}=-\frac{p_{1}}{(E_{1}+m)} \frac{(E_{1}+m)}{E^*}(E_{1})+\frac{(E_{1}+m)}{E^*} p_{1(z)} | ||
| + | \end{cases}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\Longrightarrow\begin{cases} | ||
| + | E^*_{1}=\frac{(11000 MeV+.511 MeV)}{106.031 MeV} (11000 MeV)-\frac{11000 MeV}{106.031 MeV} 11000 MeV \approx 53.015 MeV\\ | ||
| + | p^*_{1(z)}=-\frac{11000 MeV}{106.031 MeV}(11000 MeV)+\frac{(11000 MeV+.511 MeV)}{106.031 MeV} 11000 MeV \approx 53.013 MeV | ||
| + | \end{cases}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>p^*_{1} =\sqrt {(p^*_{1(x)})^2+(p^*_{1(y)})^2+(p^*_{1(z)})^2} \Longrightarrow p^*_{1}=p^*_{1(z)}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>p^*_{2} =\sqrt {(p^*_{2(x)})^2+(p^*_{2(y)})^2+(p^*_{2(z)})^2} \Longrightarrow p^*_{2}=p^*_{2(z)}</math></center> | ||
| + | |||
| + | |||
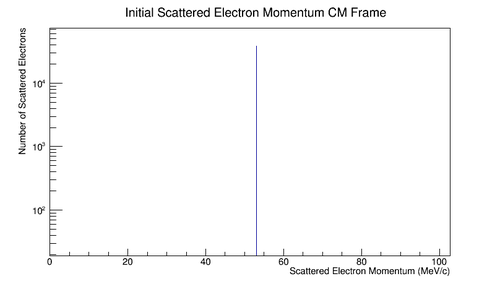
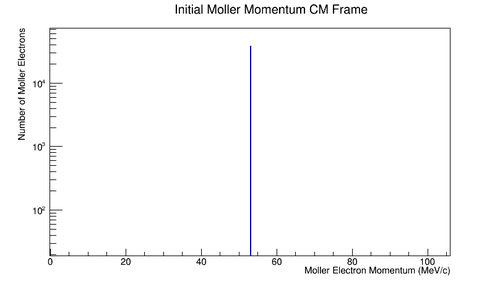
| + | This gives the momenta of the particles in the center of mass to have equal magnitude, but opposite directions. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <center><gallery widths=500px heights=400px> | ||
| + | File:Init_e_Mom_CM.png|'''Figure 5.1.3:''' Initial momentum for lab frame electron incident at 11GeV as seen in the center of mass frame. | ||
| + | File:Init_Mol_Mom_CM.png|'''Figure 5.1.4:''' Initial momentum for a lab frame stationary particle as seen in the center of mass frame. | ||
| + | </gallery></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <center><gallery widths=500px heights=400px> | ||
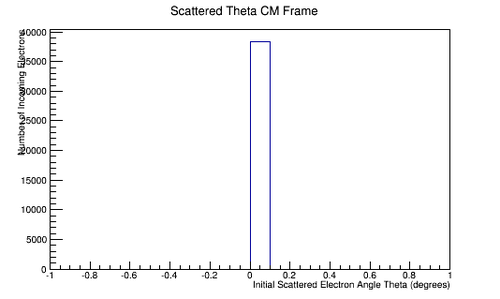
| + | File:Init_e_Theta_CM.png|'''Figure 5.1.5:''' Initial incoming angle theta for a lab frame electron incident at 11GeV as seen in the center of mass frame. | ||
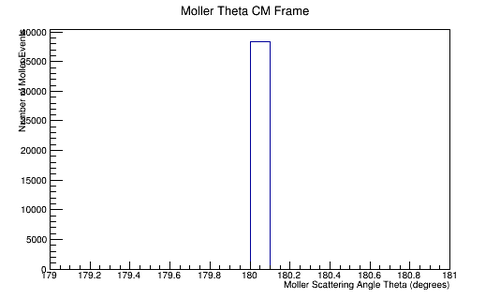
| + | File:Init_Mol_Theta_CM.png|'''Figure 5.1.6:''' Initial incoming angle theta for a lab frame stationary electron as seen in the center of mass frame. | ||
| + | </gallery></center> | ||
| − | |||
| + | ---- | ||
| − | |||
<center><math>\textbf{\underline{Navigation}}</math> | <center><math>\textbf{\underline{Navigation}}</math> | ||
| − | [[ | + | [[Uniform_distribution_in_Energy_and_Theta_LUND_files|<math>\vartriangleleft </math>]] |
| − | [[VanWasshenova_Thesis# | + | [[VanWasshenova_Thesis#Weighted_Isotropic_Distribution_in_Lab_Frame|<math>\triangle </math>]] |
| − | [[ | + | [[Phase_space_Limiting_Particles|<math>\vartriangleright </math>]] |
</center> | </center> | ||
Latest revision as of 18:36, 30 May 2017
4.1.1 Center of Mass for Stationary Target
For an incoming electron of 11GeV striking a stationary electron we would expect:
Inspecting the Lorentz transformation to the Center of Mass frame:
For the case of a stationary electron, this simplifies to:
which gives,
Solving for , with
Similarly, solving for by substituting in
Using the fact that
Using the relation
This gives the momenta of the particles in the center of mass to have equal magnitude, but opposite directions.