Difference between revisions of "Se PAA Reactions"

From New IAC Wiki
Jump to navigation Jump to search
 
(3 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
[[PAA_Selenium#Can_one_perform_PAA_measurements_of_Se-82_and_Se-76.3F]]
 
[[PAA_Selenium#Can_one_perform_PAA_measurements_of_Se-82_and_Se-76.3F]]
 +
==Single and double particle knockout reactions==
 +
 +
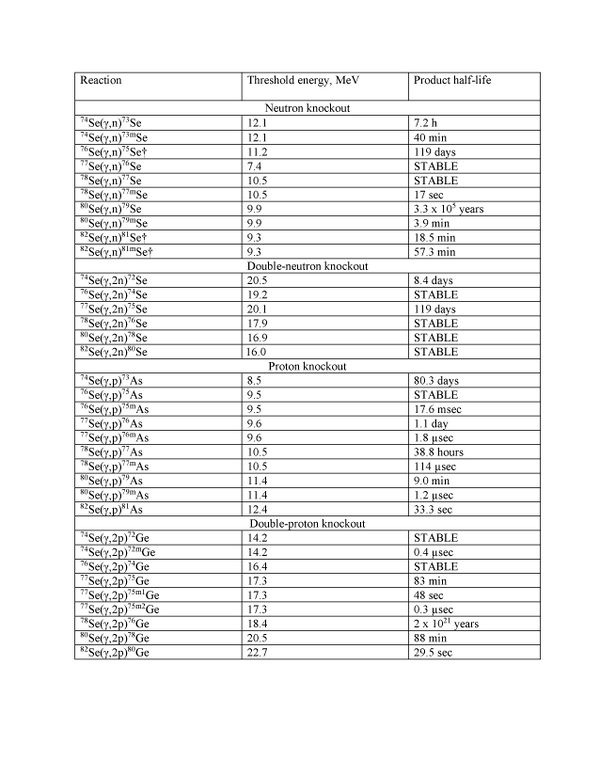
[[File:TableOfReactions.jpg|600px]]
 
==Neutron knockout of Se-82==
 
==Neutron knockout of Se-82==
 
If you knock a neutron out of Se-82 you produce the unstable isotope Se-81 which Beta emitts with half life of 18.45 min and a meta-state that emmits a 103 keV gamma with a 57.28 minute half life.  
 
If you knock a neutron out of Se-82 you produce the unstable isotope Se-81 which Beta emitts with half life of 18.45 min and a meta-state that emmits a 103 keV gamma with a 57.28 minute half life.  

Latest revision as of 16:57, 23 February 2018

PAA_Selenium#Can_one_perform_PAA_measurements_of_Se-82_and_Se-76.3F

Single and double particle knockout reactions

TableOfReactions.jpg

Neutron knockout of Se-82

If you knock a neutron out of Se-82 you produce the unstable isotope Se-81 which Beta emitts with half life of 18.45 min and a meta-state that emmits a 103 keV gamma with a 57.28 minute half life.

[math]{82 \atop 34\; }Se (\gamma,n){81 \atop \; }Se[/math]

Prominent decay photons from an IT are

276 keV and 290 keV for the 57 minute half life isotope, 566 & 828 have less than half the intensity of the 276 and 290

The minimum energy required to knock out a neutron from this isotope is

(Mass of Se-81)-(Mass of Se-82)+(Mass of 1 neutron)[MeV/c^2] = 73511.651 - 744442.2136 + 939.57 -> 9.0 MeV

you can see the line and half life in the root file /data/IAC/Se/Feb2017Run/Pure_Se_cat.root file on daq1 using the commands

MPA->Draw("-2.7285+0.815579*evt.Chan","evt.Chan>338 && evt.Chan < 344 && evt.ADCid==1");

MPA->Draw("evt.Sec/60","evt.Chan>338 && evt.Chan < 344 && evt.ADCid==1");

Neutron knockout of Se-76

If you knock a neutron out of Se-76 you produce the unstable isotope Se-75 which has a half life of 119 days.

[math]{76 \atop\; 34}Se (\gamma,n){75 \atop \; }Se[/math]

The prominent photons emitted have the following energies in order of high to low intensity

136, 264, and 279 keV

http://www.nucleide.org/DDEP_WG/Nuclides/Se-75_tables.pdf


The article below describes how plant material and soil contain Se-76 to Se-82 ratios that differ from other natural samples by 1.5%. They argue that it is due to the bacteria living in plant material.

File:Krouse CanJournChem 40 1962 p367.pdf

Plant material is a natural way to sample the selenium content to determine if there are difference isotopic ratios due to the impact of human activities on the environment.

The energy required to knock out a neutron from this isotope is

(Mass of Se-75) + (Mass of 1 neutron) - (Mass of Se-81)[MeV/c^2] = 69790.3321 + 939.57 - 70718.1 -> 11.8 MeV

Relative Yield Calculations

For this section, I am interested in finding the relative yield of Se-79 when compared to Se-81 and Se-75. Cross sections were found at this website: http://www-nds.indcentre.org.in/exfor/servlet/X4sSearch5?EntryID=220070

Cross-section

Below is a table of the cross sections for all of the reactions of interest (Se-76 -> Se-75, Se-82 -> Se-81, and Se-80 -> Se-79).

Energy (MeV) Se-80 -> Se-79 (mb) Se-76 -> Se- 75 (mb) Se-82 -> Se-81 (mb)
9.42 ** ** 5.58 +/- 0.5
9.62 ** ** 8.7 +/- 0.5
9.82 ** ** 10.8 +/- 0.5
10.02 7.1 +/- 0.2 ** 12.4 +/- 0.7
10.22 10.3 +/- 0.4 0.4 +/- 0.2 15 +/- 0.9
10.42 12.9 +/- 0.5 0.8 +/- 0.3 15.4 +/- 0.9
10.62 16.2 +/- 0.5 4.7 +/- 0.3 17.3 +/- 1.1
10.82 19.2 +/- 0.6 6.6 +/- 0.4 21 +/- 1.1
11.02 22 +/- 0.6 9.9 +/- 0.3 21.8 +/- 1.4
11.22 23.8 +/- 1 12.2 +/- 0.4 22.5 +/- 1.9
11.42 28 +/- 1 19.5 +/- 0.5 27.7 +/- 1.5
11.62 28.6 +/- 1.2 23.5 +/- 0.5 27.8 +/- 2
11.82 30.4 +/- 1.5 26.7 +/- 0.8 28.4 +/- 1.8
12.02 33 +/- 1.4 32 +/- 0.8 31.9 +/- 1.8
12.22 34.9 +/- 1.8 36.3 +/- 0.8 34.5 +/- 2.4
12.42 37.6 +/- 1.4 38.8 +/- 1.4 38.3 +/- 2.8
12.62 41.5 +/- 2 40.9 +/- 1.4 42.6 +/- 3
12.82 43.6 +/- 2.5 46.7 +/- 1.6 41 +/- 3.2
13.02 46.7 +/- 2.8 49.2 +/- 1.8 48.8 +/- 2.5
13.22 51.9 +/- 2.6 55.8 +/- 1.5 53.3 +/- 3.4
13.42 56.7 +/- 1.5 56 +/- 2.5 52.7 +/- 4.3
13.62 61.4 +/- 2.9 63.6 +/- 2.3 60.4 +/- 3.5
13.82 69.5 +/- 3.3 69.4 +/- 2.1 73.3 +/- 4.1
14.02 78.7 +/- 4.4 74.4 +/- 2.9 78.2 +/- 4.6
14.22 84.9 +/- 3.6 78 +/- 2.8 82.3 +/- 4.2
14.42 93.3 +/- 2.7 87.6 +/- 3.4 93 +/- 4.8
14.62 100.5 +/- 4 92.2 +/- 3.1 99.4 +/- 4.4
14.82 105.1 +/- 4.6 96.2 +/- 3 110.9 +/- 3.9
15.02 110.9 +/- 4.6 101.4 +/- 3.9 114.7 +/- 6.1
15.22 118.9 +/- 4.1 104.9 +/- 4.3 124.6 +/- 5.6
15.42 125.8 +/- 5.5 108.1 +/- 5.1 137.5 +/- 6.7
15.62 132.9 +/- 4.5 106.8 +/- 5 143.7 +/- 4.6
15.82 132.7 +/- 5.9 105.4 +/- 5.6 140.4 +/- 5
16.02 127.6 +/- 5.6 104.8 +/- 5 145.69 +/- 6.9
16.22 132.4 +/- 5.3 106.6 +/- 4.9 151.8 +/- 6.9
16.42 130 +/- 7.6 100.5 +/- 7.5 143 +/- 7.4
16.62 125.4 +/- 6.2 102.6 +/- 6.2 137.8 +/- 6.2
16.82 137.4 +/- 6.7 100.5 +/- 7.5 142.8 +/- 6
17.02 138.1 +/- 7.5 101 +/- 5.9 132.2 +/- 7.2
17.22 130.4 +/- 8.3 93.1 +/- 6.3 128.8 +/- 4.7
17.42 114.9 +/- 6 95.5 +/- 6.3 122.7 +/- 5.9
17.62 110.8 +/- 6 94.8 +/- 8 120.6 +/- 6.8
17.82 104.4 +/- 7.4 99.2 +/- 7.3 119.2 +/- 7.2
18.02 108.7 +/- 6.6 98.1 +/- 6.2 115.9 +/- 7
18.22 102.4 +/- 7.3 96.3 +/- 7.3 112.5 +/- 5.6
18.42 104.3 +/- 5.7 98.6 +/- 7.7 114.1 +/- 8.2
18.62 104.1 +/- 5.5 95.5 +/- 10 114.1 +/- 6.5
18.82 91.1 +/- 7.8 87.2 +/- 9.1 90.8 +/- 7.5
19.02 90.5 +/- 5.5 88.1 +/- 7.6 99.4 +/- 6.3
19.22 85.7 +/- 6.2 97 +/- 9.9 87.2 +/- 5.9
19.42 91.4 +/- 6.6 91.7 +/- 9.2 90.6 +/- 7.2
19.62 84.9 +/- 5.6 83.8 +/- 10 81.3 +/- 6.6
19.82 90.3 +/- 8.1 71.2 +/- 8 83.8 +/- 6.5
20.02 83 +/- 5.7 74.4 +/- 7.7 80 +/- 5.9
20.22 79.9 +/- 6.2 68.8 +/- 8 71.1 +/- 6.4
20.42 67.1 +/- 7.2 66.6 +/- 7 65 +/- 7.6
20.62 70.9 +/- 6.6 59.4 +/- 7.3 57 +/- 5.6
20.82 72.2 +/- 7.6 70.3 +/- 6.5 75.2 +/- 6.7
21.02 66.8 +/- 6.5 65.8 +/- 6.4 61.4 +/- 7.6
21.22 69.7 +/- 7 59.9 +/- 7.2 73.1 +/- 6.8
21.42 68.2 +/- 8.4 59.4 +/- 7 59 +/- 9.3
21.62 68.6 +/- 7.4 66.2 +/- 6.8 67.5 +/- 6.7
21.82 60.9 +/- 7.3 68 +/- 7.2 55 +/- 7.2
22.02 58.5 +/- 7.3 62.1 +/- 6.5 55.9 +/- 8.6
22.22 56 +/- 7.8 65.3 +/- 7 59.4 +/- 8.1
22.42 69.7 +/- 7.7 61.6 +/- 0.4 64 +/- 9.7
22.62 60.1 +/- 8.8 67.7 +/- 6.2 67 +/- 8.2
22.82 60.9 +/- 8.7 55.7 +/- 7.8 55.9 +/- 8.6
23.02 58.8 +/- 9.3 57.2 +/- 6.1 61.4 +/- 11.2
23.22 50.6 +/- 9.7 55.2 +/- 7.7 48.5 +/- 8.1
23.42 31.5 +/- 8.7 44.7 +/- 8.1 46.5 +/- 10.1
23.62 37.7 +/- 8.7 31.3 +/- 5.9 34 +/- 7.1
23.82 29.5 +/- 10.2 34.7 +/- 5.9 47.6 +/- 10.1
24.02 32.4 +/- 8.6 33 +/- 6.3 43.4 +/- 10.6
24.22 32.8 +/- 9.6 21.7 +/- 7.3 46.2 +/- 9.5

Similar data can be found in the link above. Below is the plot for all the reactions of interest.

Below is a plot of 3 different isotopes of selenium with their cross sections as a function of energy.

PhotonE vs XSect.png

Now to find the relative yields, I approximated the integral the above graph using a left hand Riemann sum with an interval width of 1 MeV and multiplied it by the natural abundance in the sample. Below is a table of the reactions and their integrated cross sections.


Reaction Abundance Integrated Cross Section (mb) [10->24 MeV]
Se-82(gamma,n)Se-81 8.82% 5429.19
Se-80(gamma,n)Se-79 49.8% 5249.6
Se-76(gamma,n)Se-75 9.23% 4703.1
Reaction Abundance Integrated Cross Section (mb) [10->18 MeV]
Se-82(gamma,n)Se-81 8.82% 3271.3
Se-80(gamma,n)Se-79 49.8% 3090.5
Se-76(gamma,n)Se-75 9.23% 2644.7

Below are the equations for the relative yield of each isotope.


[math]\frac{{76 \atop 34\; }Se (\gamma,n){75 \atop \;Se}}{{80 \atop 34\; }Se (\gamma,n){79 \atop \;Se}} = \frac{Abundance \times \int_{10.02}^{24.02}\sigma dE}{Abundance \times \int_{10.02}^{24.02}\sigma dE} = \frac{0.0923 \times 4703.1}{0.498 \times 5249.6} = 0.17 = \frac{\sigma_{Se-75}}{\sigma_{Se-79}}[/math]


[math]\frac{{82 \atop 34\; }Se (\gamma,n){81 \atop \;Se}}{{80 \atop 34\; }Se (\gamma,n){79 \atop \;Se}} = \frac{Abundance \times \int_{10.02}^{24.02}\sigma dE}{Abundance \times \int_{10.02}^{24.02}\sigma dE} = \frac{0.0882 \times 5429.19}{0.498 \times 5249.6} = 0.19[/math]


As of recently, the beam energy has been lowered to 18 MeV, so the relative yield for each isotope now becomes


[math]\frac{{76 \atop 34\; }Se (\gamma,n){75 \atop \;Se}}{{80 \atop 34\; }Se (\gamma,n){79 \atop \;Se}} = \frac{Abundance \times \int_{10.02}^{18.02}\sigma dE}{Abundance \times \int_{10.02}^{18.02}\sigma dE} = \frac{0.0923 \times 2644.7}{0.498 \times 3090.5} = 0.16 = \frac{\sigma_{Se-75}}{\sigma_{Se-79}}[/math]

[math]\frac{{82 \atop 34\; }Se (\gamma,n){81 \atop \;Se}}{{80 \atop 34\; }Se (\gamma,n){79 \atop \;Se}} = \frac{Abundance \times \int_{10.02}^{18.02}\sigma dE}{Abundance \times \int_{10.02}^{18.02}\sigma dE} = \frac{0.0882 \times 3271.3}{0.498 \times 3090.5} = 0.18[/math]

Activity Productions

Let

[math]N(t)[/math] = The number of activated atoms per cubic cm at time [math]t[/math]
[math]\mathcal{N}[/math] =The number density of the target = [math]\frac{\rho N_A}{A}[/math][ Atoms/cm^3]
[math]\rho[/math] = material density [g/cm^3]
[math]N_A[/math] = Avagadro's number = [math]6 \times 10^{23}[/math] g/mole
[math]A[/math] = Atomic Number
[math] \phi[/math] = incident photon flux ( photons/sec/cm/cm)


The rate of activated nuclei production is estimated by subtracting the rate of decay from the rate of production

[math]\frac{dN(t)}{dt} = N \sigma \phi - \lambda N(t)[/math]

where

[math]\lambda[/math] = half life of activated nucleus

[math]\Rightarrow N(t) = \frac{N \sigma \phi}{\lambda}\left ( 1 - e^{-\lambda t} \right )[/math]

The production rate ratio of Se-79 to Se-75 is

[math]\frac{N_{Se-79}}{N_{Se-75}} = \left ( \frac{\sigma_{Se-79}}{\sigma_{Se-75} }\right ) \left ( \frac{\lambda_{Se-75}}{\lambda_{Se-79}}\right ) = \left ( \frac{100}{15} \right ) \left ( \frac{119}{10^8} \right ) [/math]

Activity Productions

Although the investigation of provenance will involve a comparison of isotope ratios, one will need to determine the detection limit of measuring each of those isotopes.

The amount of activated nucleii, N(t), is governed by the production rate equation below.

[math]\Rightarrow N(t) = \frac{N \sigma \phi}{\lambda}\left ( 1 - e^{-\lambda t} \right )[/math]

The number of target uncle, N, is determine using

[math]N= n_T V_T \int \sigma \phi dE[/math]

[math]n_T[/math] is the number of target nucleii per volume, [math]V_T[/math] is the amount of volume irradiated


Our goal will be to determine [math]n_T[/math]

One can use Nickel as a normalization target to remove the photon flux [math](\phi)[/math] from the integral leaving just an integral over the cross section.

PAA_Selenium#Can_one_perform_PAA_measurements_of_Se-82_and_Se-76.3F

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Se_PAA_Reactions&oldid=121731"