Difference between revisions of "Wire Number Function"
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <center><math>\underline{\textbf{Navigation}}</math> | |
| + | |||
| + | [[Function_for_change_in_x%27,_Lab_frame|<math>\vartriangleleft </math>]] | ||
| + | [[VanWasshenova_Thesis#Determining_wire-theta_correspondence|<math>\triangle </math>]] | ||
| + | [[In_the_Detector_Frame|<math>\vartriangleright </math>]] | ||
| + | |||
| + | </center> | ||
| + | |||
| + | |||
| + | =Function for the wire number in the detector frame for change in <math>\phi</math> and constant <math>\theta</math> in the lab frame= | ||
Using the expression for wire number n in terms of <math>\theta</math> for the detector mid-plane where <math>\phi=0</math>: | Using the expression for wire number n in terms of <math>\theta</math> for the detector mid-plane where <math>\phi=0</math>: | ||
| Line 80: | Line 89: | ||
<center>[[File:DC_geom.png]]</center> | <center>[[File:DC_geom.png]]</center> | ||
| − | |||
| − | |||
| − | + | ---- | |
| + | |||
| + | |||
| + | <center><math>\underline{\textbf{Navigation}}</math> | ||
| + | |||
| + | [[Function_for_change_in_x%27,_Lab_frame|<math>\vartriangleleft </math>]] | ||
| + | [[VanWasshenova_Thesis#Determining_wire-theta_correspondence|<math>\triangle </math>]] | ||
| + | [[In_the_Detector_Frame|<math>\vartriangleright </math>]] | ||
| + | |||
| + | </center> | ||
Latest revision as of 20:29, 15 May 2018
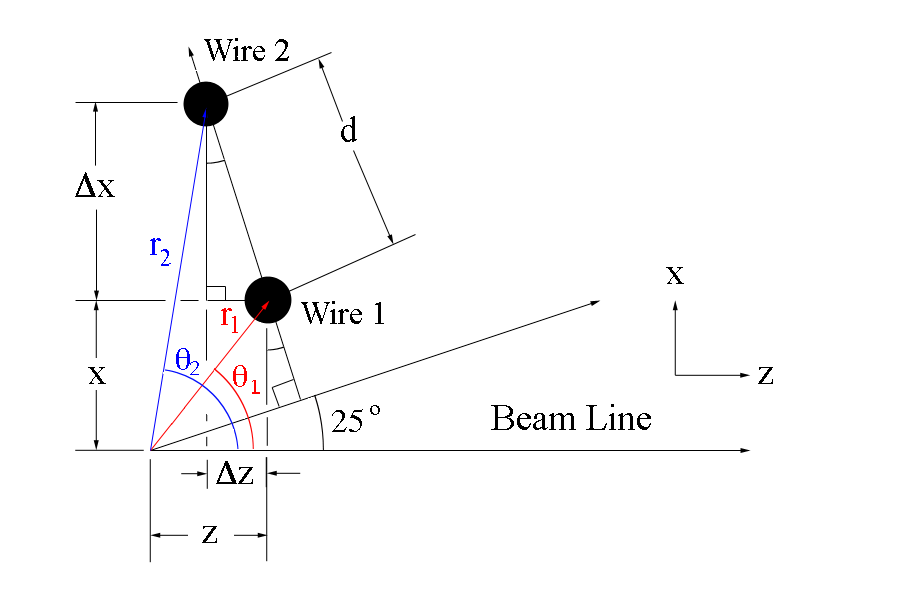
Function for the wire number in the detector frame for change in and constant in the lab frame
Using the expression for wire number n in terms of for the detector mid-plane where :
We can use the inverse of this function to find the neighboring wire's corresponding angle theta
We also know what the x' function must follow dependent on phi in the detector plane
We can take this point to be the x axis intercept and use the fact that each wire is titled by 6 degrees to the horizontal in the plane of the detector to create an equation
where the initial wire and x' position at the given theta is represented by
This equation can be solved for a hypothetical wire 0, which will allow the wire number to be the multiplicative factor for the change from the starting position.
Since each wire is separated by .01337 meters
Each wire becomes an equation of the form,
This agrees with CED simulation