Difference between revisions of "LB RunGroupC Vertex"

From New IAC Wiki
Jump to navigation Jump to search
 
(80 intermediate revisions by 2 users not shown)
Line 5: Line 5:
 
[[LB_GEMC2.4CJ2.4_Vertex]]
 
[[LB_GEMC2.4CJ2.4_Vertex]]
  
−
 
+
[[Phi angle gcard vs. LUND]]
  
  
Line 12: Line 12:
 
  Set all histogram ranges to -6,6 cm  and bin sizes of 0.1 cm
 
  Set all histogram ranges to -6,6 cm  and bin sizes of 0.1 cm
  
−
===Point target X,Y,Z=0 cm===
+
Below are some of the sample GEMC simulations as seen in the CED
−
 
 
−
 
 
−
 
 
−
Below are examples of the reconstruction for several line targets as seen in the CED
 
−
 
 
−
 
 
−
We should change it to +30,150,210, and 330 degrees so the electron is not going in between two drift chambers but rather into the center, keep 90 and 270.
 
  
  
Line 28: Line 21:
 
|-
 
|-
 
|}<br>
 
|}<br>
 +
 +
There is a bash script on lds2 that will create Vx,Vy, and Vz differences for a point target, 3 2 cm line targets (in X,Y, and Z), 2 2D targets (one XZ target where X = 2cm and Z = 6cm and another where Y = 2cm and Z = 6 cm), and one 3D target where X = Y = 2cm and Z = 6cm. A 6 GeV electron is fired at angles <math>\theta = 25</math> degrees and <math>\phi = 30</math> degrees. The path to the script is /home/lds/src/CLAS/GEMC/experiments/eg12/vertex and the file is called run.exe. To run it you must be in a tcsh and have the setup in the GEMC directory sourced. Then simply hit ./run.exe. Right now the number of events is small (100), but that can easily be changed within the script.
 +
 +
===Point target X,Y,Z=0 cm===
  
  
  
 
The histograms below are using a 6 GeV electron fired at an angles of 25 degrees in theta and 0 degrees in phi.
 
The histograms below are using a 6 GeV electron fired at an angles of 25 degrees in theta and 0 degrees in phi.
 +
 +
For the plots below, I used the following gcard, sample LUND file, and commands in GEMC 2.4, coat-java 2.4, and ROOT
 +
 +
gcard:
 +
 +
<gcard>
 +
 +
      <detector name="../../../../clas12/fc/forwardCarriage" factory="TEXT" variation="original"/>
 +
      <detector name="../../../../clas12/dc/dc"            factory="TEXT" variation="ccdb"/>
 +
      <detector name="../../../../clas12/ec/ec"            factory="TEXT" variation="original"/>
 +
      <detector name="../../../../clas12/ctof/ctof"            factory="TEXT" variation="original"/>
 +
      <detector name="../../../../clas12/ftof/ftof"            factory="TEXT" variation="java"/>
 +
      <detector name="../../../../clas12/htcc/htcc"            factory="TEXT" variation="original"/>
 +
      <detector name="../../../../clas12/pcal/pcal"            factory="TEXT" variation="javageom"/>
 +
      <detector name="../../../../clas12/magnets/solenoid" factory="TEXT" variation="original"/>
 +
      <option name="SCALE_FIELD" value="clas12-torus-big, -1"/>
 +
      <option name="HALL_FIELD"  value="clas12-solenoid"/>
 +
      <option name="OUTPUT" value="evio,eg12_sol_75k_No_Raster.ev"/>
 +
 +
</gcard>
 +
 +
Sample LUND File:
 +
 +
1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
 +
1      -1      1      11      0      0      0      2.53564      5.43788      6      0.000511      0      0      0
 +
1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
 +
1      -1      1      11      0      0      0      2.53564      5.43788      6      0.000511      0      0      0
 +
1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
 +
1      -1      1      11      0      0      0      2.53564      5.43788      6      0.000511      0      0      0
 +
 +
 +
GEMC Command:
 +
 +
~/src/CLAS/GEMC/source/gemc -USE_GUI=0 -INPUT_GEN_FILE="LUND,No_Raster.LUND" -N=75000 eg12_sol_No_Raster.gcard
 +
 +
Coat-Java 2.4 command:
 +
 +
~/src/CLAS/coatjava-2.4/bin/clas12-reconstruction -i ../files/vertex/vertex.evio -config GEOM::new=true -config MAG::torus=-1.0 -config MAG::solenoid=1.0 -o ../files/vertex/vertex_rec.evio -s DCHB:DCTB:EC:FTOF:EB -config DATA::mc=true -config DCTB::useRaster=true
 +
 +
Sample ROOT command:
 +
 +
clas12->Draw("GenPart.x - Event.x","abs(Event.x)<3");
 +
 +
 
{|border="5"
 
{|border="5"
 
! || No Rastering
 
! || No Rastering
Line 68: Line 109:
  
 
Two vertex variables are fixed at zero and the third vertex variable is altered. A 6 GeV electron was fired at angles of 25 degrees in theta and 0 degrees in phi.
 
Two vertex variables are fixed at zero and the third vertex variable is altered. A 6 GeV electron was fired at angles of 25 degrees in theta and 0 degrees in phi.
 +
 +
The gcard used had the same detector parts as above, but the filename and pathways were changed.
 +
 +
Below is a sample line from the LUND files:
 +
 +
For 2cm X Target: 1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
 +
1      -1      1      11      0      0      0      2.53564      5.43788      6      0.000511      0.999484      0      0
 +
 +
For 2cm Y Target: 1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
 +
1      -1      1      11      0      0      0      2.53564      5.43788      6      0.000511      0      0.999484      0
 +
 +
For 2cm Z Target: 1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
 +
1      -1      1      11      0      0      0      2.53564      5.43788      6      0.000511      0      0      2.99845
 +
 +
 +
Also, here are the GEMC, Coat-Java, and a sample ROOT command.
 +
 +
GEMC: ~/src/CLAS/GEMC/source/gemc -USE_GUI=0 -INPUT_GEN_FILE="LUND,test.LUND" -N=100 eg12.gcard
 +
 +
Coat-Java:~/src/CLAS/coatjava-2.4/bin/clas12-reconstruction -i ../files/vertex/vertex.evio -config GEOM::new=true -config MAG::torus=-1.0 -config MAG::solenoid=1.0 -o ../files/vertex/vertex_rec.evio -s DCHB:DCTB:EC:FTOF:EB -config DATA::mc=true -config DCTB::useRaster=true
 +
 +
Sample ROOT command: clas12->Draw("GenPart.x - Event.x","abs(Event.x)<2");
  
 
{|border="5"
 
{|border="5"
Line 86: Line 149:
  
 
=== Extended target -3 < Z < 3 cm ===
 
=== Extended target -3 < Z < 3 cm ===
−
{|border="5"
+
 
−
!  || 1cm X Raster || 1 cm Y Raster|| 1 cm X & Y Raster
+
For the plots below a 6 GeV electron was fired at angles theta = 25 degrees and phi = 0 degrees. There were 3 separate simulations ran for when -3 cm < Z < 3 cm. The first was a 2-D target with -3 cm < Z < 3 cm and -1 cm < X < 1 cm and Y = 0 cm, while the second had the same values for Z, but instead -1 cm < Y < 1cm and X = 0 cm. The final set of plots was created using -3 cm < Z < 3 cm , -1 cm < X < 1 cm, and -1 cm < Y < 1 cm.
−
|-
+
 
−
|| X Resolution (cm) || 0.2696 +/- 0.0009 || 0.2588 +/- 0.0009 || 0.2734 +/- 0.0009
+
Below are some of the sample LUND files used.
−
|-
+
 
−
|| Y Resolution (cm) || 0.6234 +/- 0.0014 || 0.6851 +/- 0.0014 || 0.6927 +/- 0.0013
+
For the XZ Target:
−
|-
+
 
−
|| Z Resolution (cm) || 1.136 +/- 0.002 || 1.361 +/- 0.002 || 1.381 +/- 0.003
+
1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
−
|-
+
1      -1      1      11      0      0      0       2.53564      5.43788      6      0.000511      -0.67418      0       2.99845
−
|| Generated Vx (cm) || [[File:3cm ZRaster 1cm XRaster GenX sol.png|200px]] || [[File:3cm ZRaster 1cm YRaster GenX sol.png|200px]] || [[File:3cm ZRaster 1cm XYRaster sol GenPartx.png|200px]]
+
1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
−
|-
+
1      -1      1      11      0      0      0       2.53564      5.43788      6      0.000511      0.894402      0      -1.30429
−
|| Generated Vy (cm) || [[File:3cm ZRaster 1cm XRaster GenY sol.png|200px]] || [[File:3cm ZRaster 1cm YRaster GenY sol.png|200px]] || [[File:3cm ZRaster 1cm XYRaster GenParty.png|200px]]
+
 
−
|-
+
For the YZ Target:
−
|| Generated Vz (cm) || [[File:3cm ZRaster 1cm XRaster GenZ sol.png|200px]] || [[File:3cm ZRaster 1cm YRaster GenZ sol.png|200px]] || [[File:3cm ZRaster 1cm XYRaster GenPartz sol.png|200px]]
+
 
−
|-
+
1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
−
|| Reconstructed Vx (cm) || [[File:3cm ZRaster 1cm XRaster EventX sol.png|200px]] || [[File:3cm ZRaster 1cm YRaster EventX sol.png|200px]] || [[File:3cm ZRaster 1cm XYRaster Eventx.png|200px]]
+
1      -1       1      11      0      0      0      2.53564      5.43788      6      0.000511      0      -0.67418      2.99845
−
|-
+
1       1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
−
|| Reconstructed Vy (cm) || [[File:3cm ZRaster 1cm XRaster EventY sol.png|200px]] || [[File:3cm ZRaster 1cm YRaster EventY sol.png|200px]] || [[File:3cm ZRaster 1cm XYRaster Eventy.png|200px]]
+
1      -1      1      11      0      0      0      2.53564      5.43788      6      0.000511      0      0.894402      -1.30429
−
|-
+
 
−
|| Reconstructed Vz (cm) || [[File:3cm ZRaster 1cm XRaster EventZ sol.png|200px]] || [[File:3cm ZRaster 1cm YRaster EventZ sol.png|200px]] || [[File:3cm ZRaster 1cm XYRaster eventz.png|200px]]
+
 
−
|-
+
For the XYZ Target:  
−
|| Vx Difference (cm) || [[File:XZRaster_VxDifference_1mmbins.png|200px]] || [[File:YZRaster_VxDifference_1mmbins.png|200px]] || [[ File:XYZRaster_VxDifference_1mmbins.png|200px]]
+
 
−
|-
+
1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
−
|| Vy Difference (cm) || [[File:XZRaster_VyDifference_1mmbins.png|200px]] || [[File:YZRaster_VyDifference_1mmbins.png|200px]] || [[File:XYZRaster_VyDifference_1mmbins.png|200px]]
+
1      -1      1      11      0      0      0      2.53564      5.43788      6      0.000511      -0.67418      -0.434764      2.99845
−
|-
+
1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
−
|| Vz Difference (cm) || [[File:XZRaster_VzDifference_1mmbins.png|200px]] || [[File:YZRaster_VzDifference_1mmbins.png|200px]] || [[File:XYZRaster_VzDifference_1mmbins.png|200px]]
+
1      -1      1      11      0      0      0      2.53564      5.43788      6      0.000511      -0.536687      -0.0300528      2.68321
−
|}<br>
+
1      1      1      1      1      1.00029 0.0718059      0.937771        1.48222 0.789865
 +
1      -1      1      11      0      0      0      2.53564      5.43788      6      0.000511      0.488611      0.0800873      2.74486
 +
 
 +
 
 +
The GEMC and Coat-Java command lines are similar to the previously seen commands. The only things that changed were the LUND file names, and the ev/evio filenames. The command lines can be seen at the top of the histograms.
 +
 
 +
[[VertREC_9-22-16_table_3ltZgt-3]]
  
 
=== Extended target in Z. Vy shift analysis ===
 
=== Extended target in Z. Vy shift analysis ===
Line 118: Line 187:
 
All Histograms below were created by simply making the target longer along the Z axis. Each case uses vertex points for X and Y ranging from -1cm to 1cm
 
All Histograms below were created by simply making the target longer along the Z axis. Each case uses vertex points for X and Y ranging from -1cm to 1cm
  
−
{|border="5"
+
[[VertREC_9-22-16_table_3ltZgt-3_1gtRlt-1]]
−
!  || 0.5cm Z Target || 1cm Z Target|| 2cm Z Target || 3cm Z Target || 4cm Z Target || 5cm Z Target
 
−
|-
 
−
|| X Resolution (cm) || 0.2705 +/- 0.0010 || 0.2726 +/- 0.0010 || 0.2716 +/- 0.0010 || 0.2731 +/- 0.0010 || 0.2702 +/- 0.0009 || 0.2736 +/- 0.0010
 
−
|-
 
−
|| Y Resolution (cm) || 0.2041 +/- 0.0010 || 0.2282 +/- 0.0011 || 0.3152 +/- 0.0014 || 0.433 +/- 0.002 || 0.5584 +/- 0.0018 || 0.6454 +/- 0.0015
 
−
|-
 
−
|| Z Resolution (cm) || 0.28 +/-0.00 || 0.3582 +/- 0.0013 || 0.5659 +/- 0.0018 || 0.7927 +/- 0.0023 || 1.034 +/- 0.003 || 1.253 +/-0.003 
 
−
|-
 
−
|| X Mean (cm) || 0.0139 +/- 0.001 || 0.0139 +/- 0.00107 || 0.01436 +/- 0.00104 || 0.01217 +/- 0.00107 || 0.00991 +/- 0.00104 || 0.009022 +/- 0.00105 
 
−
|-
 
−
|| Y Mean (cm) || -0.1893 +/- 0.0011 || -0.2004 +/- 0.0012 || -0.2379 +/- 0.0016 || -0.2936 +/- 0.0022 || -0.3648 +/- 0.0027 || -0.3871 +/- 0.0026
 
−
|-
 
−
|| Z Mean (cm) || 0.0928 +/- 0.0014 || 0.06464 +/- 0.0013 || -0.0337 +/- 0.0028 ||  -0.1582 +/- 0.0040 || -0.3016 +/- 0.0053 || -0.486 +/- 0.006
 
−
|-
 
−
|| Generated Vx (cm) || [[ File:05cmZTarg GenPartx.png|200 px]] || [[ File:1cmZTarg GenPartx.png|200px]]|| [[File:2cmZTarg GenPartx.png|200px]] ||[[ File:3cmZTarg GenPartx.png|200px]] || [[File:4cmZTarg GenPartx.png|200px]] || [[File:5cmZTarg GenPartx.png|200px]]
 
−
|-
 
−
|| Generated Vy (cm) || [[File:0.5ZTarg GenPartY.png|200px]] || [[File:1cmZTarg GenParty.png|200px]] || [[File:2cmZTarg GenPartY.png|200px]] || [[File:3cmZTarg GenParty.png|200px]] || [[File:4cmZTarg GenPartY.png|200px ]] || [[File:5cmZTarg GenPartY.png|200px]] 
 
−
|-
 
−
|| Generated Vz (cm) || [[File:05ZTarg GenPartz.png|200px]] || [[File:1cmZTarg GenPartz.png|200px]] || [[File:2cmZTarg GenPartz.png|200px]] || [[File:3cmZTarg GenPartz.png|200px]] || [[File:4cmZTarg GenPartz.png|200px]] || [[File:5cmZTarg GenPartz.png|200px]]
 
−
|-
 
−
|| Reconstructed Vx (cm) || [[File:0.5ZTarg Eventx.png|200px]] || [[File:1cmZTarg Eventx.png|200px]] || [[File:2cmZTarg Eventx.png|200px]] || [[File:3cmZTarg Eventx.png|200px]] || [[File:4cmZTarg Eventx.png|200px]] || [[File:5cmZTarg Eventx.png|200px]] 
 
−
|-
 
−
|| Reconstructed Vy (cm) || [[File:0.5ZTarg Eventy.png|200px]] || [[File:1cmZTarg Eventy.png|200px]] || [[File:2cmZTarg EventY.png|200px]] || [[File:3cmZTarg Eventy.png|200px]] || [[File:4cmZTarg Eventy.png|200px]] || [[ File:5cmZTarg EventY.png | 200px]]
 
−
|-
 
−
|| Reconstructed Vz (cm) || [[File:0.5ZTarg Eventz.png|200px]] || [[ File:1cmZTarg Eventz.png|200px]]|| [[ File:2cmZTarg Eventz.png|200px]]|| [[File:3cmZTarg Eventz.png|200px]] || [[File:4cmZTarg Eventz.png|200px]] || [[File:5cmZTarg Eventz.png|200px]]
 
−
|-
 
−
|| Vx Difference (cm) || [[File:0.5ZTarg VxDiff.png|200px]] || [[File:1cmZTarg VxDiff.png|200px]] || [[ File:2cmZTarg VxDiff.png|200px]]|| [[File:3cmZTarg VxDiff.png|200px]] || [[File:4cmZTarg VxDiff.png|200px]] || [[File:5cmZTarg VxDiff.png|200px]]
 
−
|-
 
−
|| Vy Difference (cm) || [[File:0.5ZTarg VyDiff.png|200px]] || [[File:1cmZTarg VyDiff.png|200px]] || [[ File:2cmZTarg VyDiff.png|200px]]|| [[File:3cmZTarg VyDiff.png|200px]] || [[File:4cmZTarg VyDiff.png|200px]] || [[File:5cmZTarg VyDiff.png|200px]]
 
−
|-
 
−
|| Vz Difference (cm) || [[File:0.5ZTarg VzDiff.png|200px]] || [[ File:1cmZTarg VzDiff.png|200px]]|| [[File:2cmZTarg VzDiff.png|200px]] || [[File:3cmZTarg VzDiff.png|200px]] || [[ File:4cmZTarg VzDiff.png|200px]] || [[File:5cmZTarg VzDiff.png|200px]]  
 
−
|}<br>
 
−
 
 
−
It would seem that increasing the length of the target in the Z direction has an effect on the resolution of the Y vertex position along with how far the center of the Gaussian peak will shift for the Y vertex differences.
 
  
 
=== Localized Vertex Resolution Investigation of Line Targets ===
 
=== Localized Vertex Resolution Investigation of Line Targets ===
Line 158: Line 193:
 
GEMC was ran to create electrons being produced in a line along certain axes. These include three separate 2cm targets centered at (0,0,0) in the X, Y , and Z directions. The final target is a line along the Z axis centered at (0,0,0) that is 6cm long. The generated electrons were shot at 25 degrees in theta and 0 degrees in phi at an energy of 6GeV.
 
GEMC was ran to create electrons being produced in a line along certain axes. These include three separate 2cm targets centered at (0,0,0) in the X, Y , and Z directions. The final target is a line along the Z axis centered at (0,0,0) that is 6cm long. The generated electrons were shot at 25 degrees in theta and 0 degrees in phi at an energy of 6GeV.
  
−
Here is an example of how the cuts were made. Consider the case of a 2cm line target in the Z direction centered at (0,0,0). Closed intervals begin at the end of the target and are 0.1cm long. So the first interval would be [-1.0,-0.9], then the next would be [-0.9, -0.8] and so on until the entire target is covered. The events in the EVENTHB bank were cut so that in any given interval there would be a margin of +/- 1cm to remove any outliers that may cause the histograms to have long tails.   
+
Here is an example of how the cuts were made. Consider the case of a 2cm line target in the Z direction centered at (0,0,0). Closed intervals begin at the end of the target and are 0.1cm long. So the first interval would be [-1.0,-0.9], then the next would be [-0.9, -0.8] and so on until the entire target is covered. The events in the EVENTHB bank were cut so that in any given interval there would be a margin of +/- 1cm from the end of the area of interest to remove any outliers that may cause the histograms to have long tails.   
  
  
Line 165: Line 200:
 
Below are the histograms for the 2cm line target in Y,X=0,Z=0. The electrons were fired with an energy of 6 GeV at 25 degrees in theta at 0 degrees in phi.
 
Below are the histograms for the 2cm line target in Y,X=0,Z=0. The electrons were fired with an energy of 6 GeV at 25 degrees in theta at 0 degrees in phi.
  
−
{|border="5"
+
[[2cm YLineTarg 0 Degree Rotation 09/23/16]]
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
+
 
−
|-
+
Below are the histograms for a 2cm target along the Y axis, X = 0 Z = 0. The electrons were fired with an energy of 6 GeV at 25 degrees in theta and 180 degrees in phi.
−
|| [[File:GenPart.x Local Vert.png|200px]] || [[File:GenPart.y Local Vert.png|200px]] || [[File:GenPart.z Local Vert.png|200px]] || [[ File:Event.x Local Vert.png|200px]] || [[File:Event.y Local Vert.png|200px]] || [[File:Event.z Local Vert.png|200px]]
+
 
−
|-
+
[[2cm YLineTarg 180 Degree Rotation 09/23/16]]
−
|}<br>
+
 
 +
Below are the Histograms for a 2cm long target in the X Direction with a 6GeV electron fired at 25 degrees in theta and 90 degrees in phi
 +
 
 +
[[2cm XLineTarg 90 Degree Rotation 09/23/16]]
 +
 
 +
Below are the Vx Differences using a 2cm target in X with incident 6 GeV electrons at 25 degrees in theta and 270 degrees in phi
 +
 
 +
 
 +
 
 +
[[2cm XLineTarg 270 Degree Rotation 09/23/16]]
 +
 
 +
 
 +
 
 +
Below are the histograms for a 6cm target in the Z direction using a 6 GeV electron fired at 25 degrees in theta and 0 degrees in phi.
 +
 
 +
 
 +
[[6cm ZLineTarg 0 Degree Rotation 09/23/16]]
 +
 
 +
Below are the histograms for a 6cm target in the Z direction using a 6 GeV electron fired at 25 degrees in theta and 90 degrees in phi.
 +
 
 +
 
 +
[[6cm ZLineTarg 90 Degree Rotation 09/23/16]]
 +
 
 +
 
 +
Below are the histograms for a 6 GeV electron fired at angles 25 degrees in theta and 270 degrees in phi. The target was 6cm in the Z direction.
 +
 
 +
 
 +
[[6cm ZLineTarg 270 Degree Rotation 09/23/16]]
 +
 
 +
 
 +
Below are the histograms for a 2cm target along the Y axis, X = 0 Z = 0. The electrons were fired with an energy of 6 GeV at 25 degrees in theta and 30 degrees in phi.
 +
 
 +
[[2cm YLineTarg 30 Degree Rotation 09/23/16]]
 +
 
 +
 
 +
Below are the histograms for a 2cm Y target with an incident electron energy of 6 GeV. The angles were theta = 25 degrees and phi = 210 degrees
 +
 
 +
 
 +
[[2cm YLineTarg 210 Degree Rotation 09/23/16]]
 +
 
 +
=== Localized Vertex Resolution Investigation of 2 Dimensional Targets ===
 +
The histograms below were created using a 6 GeV electron fired at 25 degrees in theta and 30 degrees in phi. To make the cuts I simply made circles of increasing radius centered at the origin. I used 0.1cm increments to make the 10 histograms for each vertex position.
 +
 
 +
Below are the Vx and Vy Differences for a 2cm XY target, Z=0.
 +
 
 +
[[2cm XYTarg Z=0 Vx and Vy Differences 09/23/16]]
  
−
{|border="5"
+
Below are the Vy and Vz differences for a 2cm target in Y and Z, X=0. The electrons were fired with an energy of 6 GeV and angles of 25 degrees in theta and 30 degrees in phi.
−
||Interval || Resolution (cm) || Vy Difference || *** || Interval || Resolution (cm) || Vy Difference
 
−
|-
 
−
||[-1.0,-0.9] || 0.09406 +/- 0.00128 ||[[ File:VyDiff--1.0,-0.9-.png|200px]]  || *** || [0.9,1.0] || 0.1001 +/- 0.0016 ||[[File:VyDiff-0.9,1.0-.png|200px]]
 
−
|-
 
−
||[-0.9,-0.8] || 0.0868 +/- 0.0013 || [[File:VyDiff--0.9,-0.8-.png|200px]] || *** || [0.8,0.9] || 0.1221 +/- 0.0018 ||[[File:VyDiff-0.8,0.9-.png|200px]]
 
−
|-
 
−
||[-0.8,-0.7] || 0.08961 +/- 0.00128 ||[[File:VyDiff--0.8,-0.7-.png|200px]] || *** || [0.7,0.8] || 0.1144 +/- 0.0017 || [[File:VyDiff-0.7,0.8-.png|200px]]
 
−
|-
 
−
||[-0.7,-0.6] || 0.09853 +/- 0.00148 ||[[File:VyDiff--0.7,-0.6-.png|200px]] || *** || [0.6,0.7] || 0.169 +/- 0.003 || [[File:VyDiff-0.6,0.7-.png|200px]]
 
−
|-
 
−
||[-0.6,-0.5] || 0.1038 +/- 0.0016 ||[[File:VyDiff--0.6,-0.5-.png|200px]] || *** || [0.5,0.6] || 0.171 +/- 0.003 ||[[File:VyDiff-0.5,0.6-.png|200px]]
 
−
|-
 
−
||[-0.5,-0.4] || 0.1202 +/- 0.0018 || [[File:VyDiff--0.5,-0.4-.png|200px]]|| *** || [0.4,0.5] || 0.1105 +/- 0.0016 ||[[File:VyDiff-0.4,0.5-.png|200px]]
 
−
|-
 
−
||[-0.4,-0.3] || 0.1755 +/- 0.0026 || [[File:VyDiff--0.4,-0.3-.png|200px]]|| *** || [0.3,0.4] || 0.09508 +/- 0.00137 ||[[File:VyDiff-0.3,0.4-.png|200px]]
 
−
|-
 
−
||[-0.3,-0.2] || 0.1847 +/- 0.0028 ||[[File:VyDiff--0.3,-0.2-.png|200px]] || *** || [0.2,0.3] || 0.09065 +/- 0.0140 ||[[File:VyDiff-0.2,0.3-.png|200px]]
 
−
|-
 
−
||[-0.2,-0.1] || 0.1255 +/- 0.0019 || [[File:VyDiff--0.2,-0.1-.png|200px]]|| *** || [0.1,0.2] || 0.093002 +/- 0.0013 ||[[ File:VyDiff-0.1,0.2-.png|200px]]
 
−
|-
 
−
||[-0.1,0.0] || 0.09663 +/- 0.00160 ||[[File:VyDiff--0.1,0.0-.png|200px]] || *** || [0.0,0.1] || 0.09008 +/- 0.0012 ||[[File:VyDiff-0.0,0.1-.png|200px]]
 
−
|-
 
−
|}<br>
 
  
−
Below are the histograms for a 2cm target along the Y axis, X = 0 Z = 0. The electrons were fired with an energy of 6 GeV at 25 degrees in theta and 180 degrees in phi.
 
  
−
{|border="5"
+
[[2cm YZTarg X=0 Vz and Vy Difference 09/23/16]]
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
−
|-
 
−
|| [[File:GenPart.x 180DegRot.png|200px]] || [[File:GenPart.y 180DegRot.png|200px]] || [[File:GenPart.z 180DegRot.png|200px|200px]] || [[File:Event.x 180DegRot.png|200px]] || [[File:Event.y 180DegRot.png|200px]] || [[File:Event.z 180DegRot.png|200px]]
 
−
|-
 
−
|}<br>
 
  
−
{|border="5"
+
Below are the Vx and Vz differences for a 2cm XZ target, Y = 0. The electrons were fired with an energy of 6 GeV at angles theta = 25 degrees and phi = 30 degrees.
−
||Interval || Resolution (cm) || Vy Difference || *** || Interval || Resolution (cm) || Vy Difference
 
−
|-
 
−
||[-1.0,-0.9] || 0.07741 +/- 0.00166 ||[[File:VyDiff--1.0,-0.9- 180Deg.png|200px]] || *** || [0.9,1.0] || 0.2319 +/- 0.0189 ||[[File:VyDiff-0.9,1.0- 180DegRot.png|200px]]
 
−
|-
 
−
||[-0.9,-0.8] || 0.0976 +/- 0.0017 ||[[File:VyDiff--0.9,-0.8- 180Deg.png|200px]] || *** || [0.8,0.9] || 0.2147 +/- 0.0185 ||[[File:VyDiff-0.8,0.9- 180DegRot.png|200px]]
 
−
|-
 
−
||[-0.8,-0.7] || 0.09924 +/- 0.00150 ||[[File:VyDiff--0.8,-0.7- 180Deg.png|200px]] || *** || [0.7,0.8] || 0.2364 +/- 0.0188 ||[[File:VyDiff-0.7,0.8- 180Deg.png|200px]]
 
−
|-
 
−
||[-0.7,-0.6] || 0.1386 +/- 0.0024 ||[[File:VyDiff--0.7,-0.6- 180Deg.png|200px]] || *** || [0.6,0.7] || 0.2323 +/- 0.0189 ||[[File:VyDiff-0.6,0.7- 180Deg.png|200px]]
 
−
|-
 
−
||[-0.6,-0.5] || 0.1278 +/- 0.0027 ||[[File:VyDiff--0.6,-0.5- 180Deg.png|200px]] || *** || [0.5,0.6] || 0.06016 +/- 0.00299 ||[[File:VyDiff-0.5,0.6- 180Deg.png|200px]]
 
−
|-
 
−
||[-0.5,-0.4] || 0.09882 +/- 0.00142 ||[[File:VyDiff--0.5,-0.4- 180Deg.png|200px]] || *** || [0.4,0.5] || 0.3986 +/- 0.00104 || [[File:VyDiff-0.4,0.5- 180Deg.png|200px]]
 
−
|-
 
−
||[-0.4,-0.3] || 0.09322 +/- 0.0013 ||[[File:VyDiff--0.4,-0.3- 180Deg.png|200px]] || *** || [0.3,0.4] || 0.3056 +/- 0.0047 ||[[File:VyDiff-0.3,0.4- 180Deg.png|200px]]
 
−
|-
 
−
||[-0.3,-0.2] || 0.09399 +/- 0.00145 ||[[File:VyDiff--0.3,-0.2- 180Deg.png|200px]] || *** || [0.2,0.3] || 0.1097 +/- 0.0029 ||[[File:VyDiff-0.2,0.3- 180Deg.png|200px]]
 
−
|-
 
−
||[-0.2,-0.1] || 0.08935 +/- 0.00131 ||[[File:VyDiff--0.2,-0.1- 180Deg.png|200px]] || *** || [0.1,0.2] || 0.1146 +/- 0.0025 ||[[File:VyDiff-0.1,0.2- 180Deg.png|200px]]
 
−
|-
 
−
||[-0.1,0.0] || 0.08913 +/- 0.00130 ||[[File:VyDiff--0.1,0.0- 180Deg.png|200px]] || *** || [0.0,0.1] || 0.09557 +/- 0.0015 ||[[File:VyDiff-0.0,0.1- 180Deg.png|200px]]
 
−
|-
 
−
|}<br>
 
  
  
 +
[[2cm XZTarg Y=0 Vx and Vz Differences 09/23/16]]
  
−
Below are the Histograms for a 2cm long target in the X Direction with a 6GeV electron fired at 25 degrees in theta and 90 degrees in phi
+
===Localized Vertex Resolution of 3 Dimensional targets===
  
−
{|border="5"
 
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
−
|-
 
−
|| [[File:GenPart.x 90DegRot.png|200px]] || [[File:GenPart.y 90DegRot.png|200px]] || [[File:GenPart.z 90DegRot.png|200px]] || [[File:Event.x 90DegRot.png|200px]] || [[File:Event.y 90DegRot.png|200px]] || [[File:Event.z 90DegRot.png|200px]]
 
−
|-
 
−
|}<br>
 
  
−
{|border="5"
+
For the plots below, a 6 GeV electron was fired at angles 25 degrees in theta and 30 degrees in phi. The target has an XY radius of 1cm and a length in the Z direction of 6cm. Setting GenPart.z = 0cm, the resolution was investigated as a function of the target's XY radius along with a table for the values.
−
||Interval || Resolution (cm) || Vx Difference || *** || Interval || Resolution (cm) || Vx Difference
 
−
|-
 
−
||[-1.0,-0.9] ||0.1341 +/- 0.0140  ||[[File:VxDiff--1.0,-0.9-.png|200px]] || *** || [0.9,1.0] || 0.01572 +/- 0.0002 ||[[File:VxDiff-0.9,1.0-.png|200px]]
 
−
|-
 
−
||[-0.9,-0.8] || 0.1304 +/- 0.0051 ||[[File:VxDiff--0.9,-0.8-.png|200px]] || *** || [0.8,0.9] || 0.01844 +/- 0.00031 ||[[File:VxDiff-0.8,0.9-.png|200px]]
 
−
|-
 
−
||[-0.8,-0.7] || 0.1182 +/- 0.0036 ||[[File:VxDiff--0.8,-0.7-.png|200px]] || *** || [0.7,0.8] || 0.01722 +/- 0.0028 ||[[File:VxDiff-0.7,0.8-.png|200px]]
 
−
|-
 
−
||[-0.7,-0.6] || 0.09062 +/- 0.0031 ||[[File:VxDiff--0.7,-0.6-.png|200px]] || *** || [0.6,0.7] || 0.02386 +/- 0.00088 ||[[File:VxDiff-0.6,0.7-.png|200px]]
 
−
|-
 
−
||[-0.6,-0.5] || 0.06816 +/- 0.00191 || [[File:VxDiff--0.6,-0.5-.png|200px]]|| *** || [0.5,0.6] || 0.024 +/- 0.001 ||[[File:VxDiff-0.5,0.6-.png|200px]]
 
−
|-
 
−
||[-0.5,-0.4] || n/a ||[[File:VxDiff--0.5,-0.4-.png|200px]] || *** || [0.4,0.5] || 0.04406 +/- 0.00182 ||  [[File:VxDiff-0.4,0.5-.png|200px]]
 
−
|-
 
−
||[-0.4,-0.3] || 0.0635 +/- 0.0013 ||[[File:VxDiff--0.4,-0.3-.png|200px]] || *** || [0.3,0.4] || 0.04517 +/- 0.00118 || [[File:VxDiff-0.3,0.4-.png|200px]]
 
−
|-
 
−
||[-0.3,-0.2] || 0.0618 +/- 0.0012 || [[File:VxDiff--0.3,-0.2-.png|200px]] || *** || [0.2,0.3] || 0.04722 +/- 0.00107 ||[[File:VxDiff-0.2,0.3-.png|200px]]
 
−
|-
 
−
||[-0.2,-0.1] || 0.07473 +/- 0.00178 ||[[File:VxDiff--0.2,-0.1-.png|200px]] || *** || [0.1,0.2] || 0.05667 +/- 0.00106 ||[[File:VxDiff-0.1,0.2-.png|200px]]
 
−
|-
 
−
||[-0.1,0.0] || 0.08787 +/- 0.00132 ||[[File:VxDiff--0.1,0.0-.png|200px]] || *** || [0.0,0.1] || 0.08356 +/- 0.00159 ||[[File:VxDiff-0.0,0.1-.png|200px]]
 
−
|-
 
−
|}<br>
 
  
−
Below are the Vx Differences using a 2cm target in X with incident 6 GeV electrons at 25 degrees in theta and 270 degrees in phi
+
In this section, concentric rings with a thickness of 0.1cm were created within the target. For example these plots would include a ring centered at x=y=z=0 and include all GenPart.x and GenPart.y from (0.0 cm, 0.1 cm), then another ring would include all Genpart.x and GenPart.y events from (0.1 cm, 0.2 cm) and so on until we reach the edge of the target. Below is a visualization of the cuts as seen in a 2D cross section of the target.
  
 +
[[File:2DTargAnnularCuts.png|200px]]
  
 +
[[File:AnnularRad vs Sigma z=0.png|200px]]
  
−
{|border="5"
+
clas12->Draw("Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.95 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.85");
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
−
|-
 
−
|| [[ File:GenPart.x 270DegRot.png|200px]] || [[ File:GenPart.y 270DegRot.png|200px]] || [[File:GenPart.z 270DegRot.png|200px]] || [[File:Event.x 270DegRot.png|200px]] || [[File:Event.y 270DegRot.png|200px]] || [[File:Event.z 270DegRot.png|200px]]
 
−
|-
 
−
|}<br>
 
  
 
{|border="5"
 
{|border="5"
−
||Interval || Resolution (cm) || Vx Difference || *** || Interval || Resolution (cm) || Vx Difference
 
−
|-
 
−
||[-1.0,-0.9] || 0.01571 +/- 0.0002 ||[[File:VxDiff--1.0,-0.9- 270Deg.png|200px]] || *** || [0.9,1.0] || 0.1257 +/- 0.0100 ||[[File:VxDiff-0.9,1.0- 270Deg.png|200px]]
 
−
|-
 
−
||[-0.9,-0.8] || 0.0163 +/- 0.0003 ||[[File:VxDiff--0.9,-0.8- 270Deg.png|200px]] || *** || [0.8,0.9] || 0.112 +/- 0.004 ||[[File:VxDiff-0.8,0.9- 270Deg.png|200px]]
 
−
|-
 
−
||[-0.8,-0.7] || 0.01821 +/- 0.0003 ||[[File:VxDiff--0.8,-0.7- 270Deg.png|200px]] || *** || [0.7,0.8] || 0.1162 +/- 0.0034 ||[[File:VxDiff-0.7,0.8- 270Deg.png|200px]]
 
−
|-
 
−
||[-0.7,-0.6] || 0.03065 +/- .000163 ||[[File:VxDiff--0.7,-0.6- 270Deg.png|200px]] || *** || [0.6,0.7] || 0.08958 +/- 0.00316 ||[[File:VxDiff-0.6,0.7- 270Deg.png|200px]]
 
−
|-
 
−
||[-0.6,-0.5] || 0.02109 +/- 0.00217 ||[[File:VxDiff--0.6,-0.5- 270Deg.png|200px]] || *** || [0.5,0.6] || 0.07347 +/- 0.00210 ||[[File:VxDiff-0.5,0.6- 270Deg.png|200px]]
 
−
|-
 
−
||[-0.5,-0.4] || 0.03772 +/- 0.00133 ||[[File:VxDiff--0.5,-0.4- 270Deg.png|200px]] || *** || [0.4,0.5] || 0.07271 +/- 0.00159 ||[[File:VxDiff-0.4,0.5- 270Deg.png|200px]] 
 
−
|-
 
−
||[-0.4,-0.3] || 0.04817 +/- 0.00125 ||[[File:VxDiff--0.4,-0.3- 270Deg.png|200px]] || *** || [0.3,0.4] || 0.06196 +/- 0.00146 || [[File:VxDiff-0.3,0.4- 270Deg.png|200px]]
 
−
|-
 
−
||[-0.3,-0.2] || 0.05154 +/- 0.00113 || [[File:VxDiff--0.3,-0.2- 270Deg.png|200px]] || *** || [0.2,0.3] || 0.06087 +/- 0.00114 ||[[File:VxDiff-0.2,0.3- 270Deg.png|200px]]
 
 
|-
 
|-
−
||[-0.2,-0.1] || 0.05677 +/- 0.00106 ||[[File:VxDiff--0.2,-0.1- 270Deg.png|200px]] || *** || [0.1,0.2] || 0.07298 +/- 0.00149 ||[[File:VxDiff-0.1,0.2- 270Deg.png|200px]]
+
||R (cm) || 0.05 +/- 0.05 || 0.15 +/- 0.05 || 0.25 +/- 0.05 || 0.35 +/- 0.05  || 0.45 +/- 0.05 ||0.55 +/- 0.05||0.65 +/- 0.05||0.75 +/- 0.05||0.85 +/- 0.05||0.95 +/- 0.05
 
|-
 
|-
−
||[-0.1,0.0] || 0.08348 +/- 0.00144 ||[[File:VxDiff--0.1,0.0- 270Deg.png|200px]] || *** || [0.0,0.1] || 0.09017 +/- 0.00128 ||[[File:VxDiff-0.0,0.1- 270Deg.png|200px]]
+
||Width (cm) || 0.05094 +/- 0.0019 || 0.07812 +/- 0.0018 || 0.3688 +/- 0.0063 || 0.5231 +/- 0.0077 || 0.718 +/- 0.012 || 0.7987 +/- 0.0092 || 0.8709 +/- 0.0085 || 1.038 +/- 0.01 || 1.183 +/- 0.012 || 1.296 +/- 0.013
 
|-
 
|-
 
|}<br>
 
|}<br>
  
 +
For the next set of plots, the GEMC simulations had the same energy and angles as above. To construct scatter plots, similar annular cuts in the radius were made (similar to above), but this time the thickness of each ring was 0.2 cm (to ensure enough events were present). In addition, the target will become extended in Z. Cuts were made in Z by restricting GenPart.z to be within a range of certain values. Each "washer" shape has a thickness of 0.5 cm in the Z direction. Histograms were created using the following command line as an example
  
 +
clas12->Draw("GenPart.z - Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.2 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.0 && GenPart.z > 0.0 && GenPart.z < 0.5");
  
  
−
Below are the histograms for a 6cm target in the Z direction using a 6 GeV electron fired at 25 degrees in theta and 0 degrees in phi.
+
Below is a plot and a table for the Radius vs. Sigma of GenPart.z - Event.z for several cuts in Z. For the plot each Radius is centered at the point plotted with a width of +/- 0.1 cm.
  
 +
[[File:Radius vs sigma pos half.png|200px]]
  
 
{|border="5"
 
{|border="5"
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
 
|-
 
|-
−
||[[File:GenPart.x 6cmZTarg NoRot.png|200px]] || [[File:GenPart.y 6cmZTarg NoRot.png|200px]] || [[File:GenPart.z 6cmZTarg NoRot.png|200px]] || [[File:Event.x 6cmZTarg NoRot.png|200px]] || [[File:Event.y 6cmZTarg NoRot.png|200px]] || [[ File:Event.z 6cmZTarg NoRot.png|200px]]
+
|| Z = (0.0 cm, 0.5 cm)
 
|-
 
|-
−
|}<br>
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
−
 
 
−
{|border="5"
 
−
||Interval || Resolution (cm) || Vz Difference || *** || Interval || Resolution (cm) || Vz Difference
 
 
|-
 
|-
−
||[-3.0,-2.5] || 0.1427 +/- 0.0009  || [[File:VzDiff--3.0,-2.5- NoRot.png|200px]]  || *** || [2.5,3.0] || 0.1467 +/- 0.0008 || [[File:VzDiff-2.5,3.0- NoRot.png|200px]]
+
||Sigma (cm) || 0.1548 +/- 0.0106 || 0.1825 +/- 0.0086 || 0.2167 +/- 0.0078 || 0.26 +/- 0.01 || 0.2774 +/- 0.0075
 
|-
 
|-
−
||[-2.5,-2.0] || 0.1412 +/- 0.0008 || [[File:VzDiff--2.5,-2.0- NoRot.png|200px]] || *** || [2.0,2.5] || 0.1419 +/- 0.0009  || [[File:VzDiff-2.0,2.5- NoRot.png|200px]]
+
||*******************************************
 
|-
 
|-
−
||[-2.0,-1.5] || 0.1365 +/- 0.0007 || [[ File:VzDiff--2.0,-1.5- NoRot.png|200px]]|| *** || [1.5,2.0] || 0.1372 +/- 0.0008  || [[ File:VzDiff-1.5,2.0- NoRot.png|200px]]
+
|| Z = (0.5 cm, 1.0 cm)
 
|-
 
|-
−
||[-1.5,-1.0] || 0.1439 +/- 0.0008 || [[File:VzDiff--1.5,-1.0- NoRot.png|200px]] || *** || [1.0,1.5] || 0.1394 +/- 0.0008  || [[File:VzDiff-1.0,1.5- NoRot.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
−
||[-1.0,-0.5] || 0.1429 +/- 0.0008 || [[File:VzDiff--1.0,-0.5- NoRot.png|200px]] || *** || [0.5,1.0] || 0.1584 +/- 0.0010 ||  [[File:VzDiff-0.5,1.0- NoRot.png|200px]]
+
||Sigma (cm) || 0.1672 +/- 0.0109 || 0.1636 +/- 0.0064 || 0.2277 +/- 0.0075 || 0.3203 +/- 0.0107 || 0.3287 +/- 0.0082
−
|-
 
−
||[-0.5,0.0] || 0.1332 +/- 0.0007  || [[File:VzDiff--0.5,0.0- NoRot.png|200px]] || *** || [0.0,0.5] || 0.1378 +/- 0.0009 || [[File:VzDiff-0.0,0.5- NoRot.png|200px]]
 
−
|-
 
−
|}<br>
 
−
 
 
−
 
 
−
Below are the histograms for a 6cm target in the Z direction using a 6 GeV electron fired at 25 degrees in theta and 90 degrees in phi.
 
−
 
 
−
 
 
−
{|border="5"
 
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
−
|-
 
−
|| [[ File:GenPart.x 90DegRot 6cmZTarg.png|200px]] || [[File:GenPart.y 90DegRot 6cmZTarg.png|200px]] ||[[File:GenPart.z 90DegRot 6cmZTarg.png|200px]]  || [[File:Event.x 90DegRot 6cmZTarg.png|200px]] || [[File:Event.y 90DegRot 6cmZTarg.png|200px]] || [[ File:Event.z 90DegRot 6cmZTarg.png|200px]]
 
−
|-
 
−
|}<br>
 
−
 
 
−
{|border="5"
 
−
||Interval || Resolution (cm) || Vz Difference || *** || Interval || Resolution (cm) || Vz Difference
 
 
|-
 
|-
−
||[-3.0,-2.5] || 0.1192 +/- 0.0005 || [[File:VzDiff--3.0,-2.5- 90DegRot.png|200px]]  || *** || [2.5,3.0] || 0.1211 +/- 0.0005 || [[File:VzDiff-2.5,3.0- 90DegRot.png|200px]]
+
||*******************************************
 
|-
 
|-
−
||[-2.5,-2.0] || 0.1205 +/- 0.0005 || [[File:VzDiff--2.5,-2.0- 90DegRot.png|200px]] || *** || [2.0,2.5] || 0.1251 +/- 0.0005 || [[File:VzDiff-2.0,2.5- 90DegRot.png|200px]]
+
||Z = (1.0 cm, 1.5 cm)
 
|-
 
|-
−
||[-2.0,-1.5] || 0.122 +/- 0.001 || [[File:VzDiff--2.0,-1.5- 90DegRot.png|200px]] || *** || [1.5,2.0] || 0.1312 +/- 0.0006 || [[File:VzDiff-1.5,2.0- 90DegRot.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
−
||[-1.5,-1.0] || 0.1249 +/- 0.0006 || [[File:VzDiff--1.5,-1.0- 90DegRot.png|200px]] || *** || [1.0,1.5] || 0.1233 +/- 0.0005 || [[File:VzDiff-1.0,1.5- 90DegRot.png|200px]]
+
||Sigma (cm) || 0.1282 +/- 0.0068 || 0.1551 +/- 0.0042 || 0.1842 +/- 0.0052 || 0.2172 +/- 0.0069 || 0.2587 +/- 0.0072
 
|-
 
|-
−
||[-1.0,-0.5] || 0.1278 +/- 0.0006 || [[File:VzDiff--1.0,-0.5- 90DegRot.png|200px]] || *** || [0.5,1.0] || 0.1254 +/- 0.0005 || [[File:VzDiff-0.5,1.0- 90DegRot.png|200px]]
+
||*******************************************
 
|-
 
|-
−
||[-0.5,0.0] || 0.1289 +/- 0.0006 || [[File:VzDiff--0.5,.0.0- 90DegRot.png|200px]] || *** || [0.0,0.5] || 0.1237 +/- 0.0005 || [[ File:VzDiff-0.0,0.5- 90DegRot.png|200px]]
+
||Z = (1.5 cm, 2.0 cm)
 
|-
 
|-
−
|}<br>
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
−
 
 
−
 
 
−
Below are the histograms for a 6 GeV electron fired at angles 25 degrees in theta and 270 degrees in phi. The target was 6cm in the Z direction.
 
−
{|border="5"
 
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
 
|-
 
|-
−
|| [[File:GenPart.x 6cm ZTarg 270DegRot.png|200px]] || [[File:GenPart.y 6cm ZTarg 270DegRot.png|200px]] || [[File:GenPart.z 6cm ZTarg 270DegRot.png|200px]] || [[File:Event.x 6cm ZTarg 270Rot.png|200px]] || [[File:Event.y 6cm ZTarg 270DegRot.png|200px]] || [[File:Event.z 6cm ZTarg 270DegRot.png|200px]]
+
||Sigma (cm) || 0.1264 +/- 0.0071 || 0.1558 +/- 0.0042 || 0.1795 +/- 0.0043 || 0.2034 +/- 0.0049 || 0.2391 +/- 0.0055
 
|-
 
|-
−
|}<br>
+
||*******************************************
−
 
 
−
{|border="5"
 
−
||Interval || Resolution (cm) || Vz Difference || *** || Interval || Resolution (cm) || Vz Difference
 
 
|-
 
|-
−
||[-3.0,-2.5] || 0.1171 +/- 0.0008 || [[File:VzDiff--3.0,-2.5- 270DegRot.png|200px]]  || *** || [2.5,3.0] || 0.1186 +/- 0.0008 || [[File:VzDiff-2.5,3.0- 270DegRot.png|200px]]
+
||Z = (2.0 cm, 2.5 cm)
 
|-
 
|-
−
||[-2.5,-2.0] || 0.1162 +/- 0.0008 || [[File:VzDiff--2.5,-2.0- 270DegRot.png|200px]] || *** || [2.0,2.5] || 0.1226 +/- 0.0009 || [[File:VzDiff-2.0,2.5- 270DegRot.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
−
||[-2.0,-1.5] || 0.1207 +/- 0.0009 ||[[File:VzDiff--2.0,-1.5- 270DegRot.png|200px]] || *** || [1.5,2.0] || 0.1317 +/- 0.0010  || [[File:VzDiff-1.5,2.0- 270DegRot.png|200px]]
+
||Sigma (cm) || 0.1723 +/- 0.0120 || 0.1519 +/- 0.0038 || 0.1896 +/- 0.0048 || 0.2033 +/- 0.0043 || 0.2361 +/- 0.0048
 
|-
 
|-
−
||[-1.5,-1.0] || 0.1294 +/- 0.0010 || [[File:VzDiff--1.5,-1.0- 270DegRot.png|200px]] || *** || [1.0,1.5] || 0.1239 +/- 0.0009 || [[File:VzDiff-1.0,1.5- 270DegRot.png|200px]]
+
||*******************************************
 
|-
 
|-
−
||[-1.0,-0.5] || 0.131 +/- 0.001 || [[File:VzDiff--1.0,-0.5- 270DegRot.png|200px]] || *** || [0.5,1.0] || 0.1256 +/- 0.0009 || [[File:VzDiff-0.5,1.0- 270DegRot.png|200px]]
+
||Z = (2.5 cm, 3.0 cm)
 
|-
 
|-
−
||[-0.5,0.0] || 0.131 +/- 0.001 || [[File:VzDiff--0.5,0.0- 270DegRot.png|200px]] || *** || [0.0,0.5] || 0.1261 +/- 0.0010 || [[File:VzDiff-0.0,0.5- 270DegRot.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
 +
||Sigma (cm) || 0.1273 +/- 0.0054 || 0.1665 +/- 0.0057 || 0.1936 +/- 0.0041 || 0.2143 +/- 0.0042 || 0.2337 +/- 0.0050
 
|}<br>
 
|}<br>
  
 +
Here is where the problem of a bimodal distribution become relevant as seen below in the histogram.
 +
 +
[[File:GenPart.z - Event.z bimodal example.png|200px]]
 +
 +
For now I will simply fit the larger peak to hopefully get rid of the muddling of the resolution, but this must be noted and investigated further later.
 +
 +
Below is the plot and the table for the negative half of the target.
 +
 +
[[File:Radius vs sigma neg half.png|200px]]
  
  
−
Below are the histograms for a 6 GeV electron fired at 25 degrees in theta and 0 degrees in phi. The target is 2cm long on the Y axis.
 
−
{|border="5"
 
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
−
|-
 
−
|| [[File:GenPart.x Local Vert.png|200px]] || [[File:GenPart.y Local Vert.png|200px]] || [[File:GenPart.z Local Vert.png|200px]] || [[ File:Event.x Local Vert.png|200px]] || [[File:Event.y Local Vert.png|200px]] || [[File:Event.z Local Vert.png|200px]]
 
−
|-
 
−
|}<br>
 
  
 
{|border="5"
 
{|border="5"
−
||Interval || Resolution (cm) || Vy Difference || *** || Interval || Resolution (cm) || Vy Difference
 
 
|-
 
|-
−
||[-1.0,-0.9] || 0.09406 +/- 0.00128 ||[[ File:VyDiff--1.0,-0.9-.png|200px]]  || *** || [0.9,1.0] || 0.1001 +/- 0.0016 ||[[File:VyDiff-0.9,1.0-.png|200px]]
+
|| Z = (-0.5 cm, 0.0 cm)
 
|-
 
|-
−
||[-0.9,-0.8] || 0.0868 +/- 0.0013 || [[File:VyDiff--0.9,-0.8-.png|200px]] || *** || [0.8,0.9] || 0.1221 +/- 0.0018 ||[[File:VyDiff-0.8,0.9-.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
−
||[-0.8,-0.7] || 0.08961 +/- 0.00128 ||[[File:VyDiff--0.8,-0.7-.png|200px]] || *** || [0.7,0.8] || 0.1144 +/- 0.0017 || [[File:VyDiff-0.7,0.8-.png|200px]]
+
||Sigma (cm) || 0.1666 +/- 0.0128 || 0.1722 +/- 0.0078 || 0.1983 +/- 0.0067 || 0.2193 +/- 0.0060 || 0.2554 +/- 0.0068
 
|-
 
|-
−
||[-0.7,-0.6] || 0.09853 +/- 0.00148 ||[[File:VyDiff--0.7,-0.6-.png|200px]] || *** || [0.6,0.7] || 0.169 +/- 0.003 || [[File:VyDiff-0.6,0.7-.png|200px]]
+
||*******************************************
 
|-
 
|-
−
||[-0.6,-0.5] || 0.1038 +/- 0.0016 ||[[File:VyDiff--0.6,-0.5-.png|200px]] || *** || [0.5,0.6] || 0.171 +/- 0.003 ||[[File:VyDiff-0.5,0.6-.png|200px]]
+
|| Z = (-1.0 cm, -0.5 cm)
 
|-
 
|-
−
||[-0.5,-0.4] || 0.1202 +/- 0.0018 || [[File:VyDiff--0.5,-0.4-.png|200px]]|| *** || [0.4,0.5] || 0.1105 +/- 0.0016 ||[[File:VyDiff-0.4,0.5-.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
−
||[-0.4,-0.3] || 0.1755 +/- 0.0026 || [[File:VyDiff--0.4,-0.3-.png|200px]]|| *** || [0.3,0.4] || 0.09508 +/- 0.00137 ||[[File:VyDiff-0.3,0.4-.png|200px]]
+
||Sigma (cm) || 0.1435 +/- 0.0069 || 0.1708 +/- 0.0068 || 0.2008 +/- 0.0069 || 0.2094 +/- 0.0058 || 0.2544 +/- 0.0065
 
|-
 
|-
−
||[-0.3,-0.2] || 0.1847 +/- 0.0028 ||[[File:VyDiff--0.3,-0.2-.png|200px]] || *** || [0.2,0.3] || 0.09065 +/- 0.0140 ||[[File:VyDiff-0.2,0.3-.png|200px]]
+
||*******************************************
 
|-
 
|-
−
||[-0.2,-0.1] || 0.1255 +/- 0.0019 || [[File:VyDiff--0.2,-0.1-.png|200px]]|| *** || [0.1,0.2] || 0.093002 +/- 0.0013 ||[[ File:VyDiff-0.1,0.2-.png|200px]]
+
||Z = (-1.5 cm, -1.0 cm)
 
|-
 
|-
−
||[-0.1,0.0] || 0.09663 +/- 0.00160 ||[[File:VyDiff--0.1,0.0-.png|200px]] || *** || [0.0,0.1] || 0.09008 +/- 0.0012 ||[[File:VyDiff-0.0,0.1-.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
−
|-
 
−
|}<br>
 
−
 
 
−
Below are the histograms for a 2cm target along the Y axis, X = 0 Z = 0. The electrons were fired with an energy of 6 GeV at 25 degrees in theta and 30 degrees in phi.
 
−
 
 
−
{|border="5"
 
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
 
|-
 
|-
−
|| [[File:GenPart.x 2cmYTarg 30DegRot.png|200px]] || [[File:GenPart.y 2cmYTarg 30DegRot.png|200px]] || [[File:GenPart.z 2cmYTarg 30DegRot.png|200px]]  || [[File:Event.x 2cmYTarg 30DegRot.png|200px]] || [[File:Event.y 2cmYTarg 30DegRot.png|200px]] || [[File:Event.z 2cmYTarg 30DegRot.png|200px]]
+
||Sigma (cm) || 0.1418 +/- 0.0073 || 0.1551 +/- 0.0047 || 0.2342 +/- 0.0092 || 0.2286 +/- 0.0066 || 0.2459 +/- 0.0066
 
|-
 
|-
−
|}<br>
+
||*******************************************
−
 
 
−
{|border="5"
 
−
||Interval || Resolution (cm) || Vy Difference || *** || Interval || Resolution (cm) || Vy Difference
 
 
|-
 
|-
−
||[-1.0,-0.9] || 0.069 +/- 0.002 || [[File:VyDiff--1.0,-0.9- 30DegRot.png|200px]] || *** || [0.9,1.0] || 0.04936 +/- 0.00068  || [[File:VyDiff-0.9,1.0- 30DegRot.png|200px]]
+
||Z = (-2.0 cm, -1.5 cm)
 
|-
 
|-
−
||[-0.9,-0.8] || 0.08185 +/- 0.00218 ||[[File:VyDiff--0.9,-0.8- 30DegRot.png|200px]] || *** || [0.8,0.9] || 0.05797 +/- 0.00094 || [[File:VyDiff-0.8,0.9- 30DegRot.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9  
 
|-
 
|-
−
||[-0.8,-0.7] || 0.08764 +/- 0.00212 || [[File:VyDiff--0.8,-0.7- 30DegRot.png|200px]] || *** || [0.7,0.8] || 0.05896 +/- 0.00086 || [[File:VyDiff-0.7,0.8- 30DegRot.png|200px]]
+
||Sigma (cm) || 0.1562 +/- 0.0091 || 0.1628 +/- 0.0045 || 0.2115 +/- 0.0076 || 0.2061 +/- 0.0056 || 0.2335 +/- 0.0077
 
|-
 
|-
−
||[-0.7,-0.6] || 0.09158 +/- 0.00258 ||[[File:VyDiff--0.7,-0.6- 30DegRot.png|200px]] || *** || [0.6,0.7] || 0.05895 +/- 0.00091 || [[File:VyDiff-0.6,0.7- 30DegRot.png|200px]]
+
||*******************************************
 
|-
 
|-
−
||[-0.6,-0.5] || 0.07913 +/- 0.00166 || [[File:VyDiff--0.6,-0.5- 30DegRot.png|200px]] || *** || [0.5,0.6] || 0.05943 +/- 0.00096 || [[File:VyDiff-0.5,0.6- 30DegRot.png|200px]]
+
||Z = (-2.5 cm, -2.0 cm)
 
|-
 
|-
−
||[-0.5,-0.4] || 0.0774 +/- 0.0014 || [[File:VyDiff--0.5,-0.4- 30DegRot.png|200px]] || *** || [0.4,0.5] || 0.06227 +/- 0.00118 || [[File:VyDiff-0.4,0.5- 30DegRot.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
−
||[-0.4,-0.3] || 0.07978 +/- 0.00157 || [[File:VyDiff--0.4,-0.3- 30DegRot.png|200px]] || *** || [0.3,0.4] || 0.08115 +/- 0.00186 || [[File:VyDiff-0.3,0.4- 30DegRot.png|200px]]
+
||Sigma (cm) || 0.1312 +/- 0.0059 || 0.1517 +/- 0.0040 || 0.2061 +/- 0.0049 || 0.257 +/- 0.008 || 0.2484 +/- 0.005
 
|-
 
|-
−
||[-0.3,-0.2] || 0.08193 +/- 0.00235 || [[ File:VyDiff--0.3,-0.2- 30DegRot.png|200px]]|| *** || [0.2,0.3] || 0.01028 +/- 0.0029 || [[File:VyDiff-0.2,0.3- 30DegRot.png|200px]]
+
||*******************************************
 
|-
 
|-
−
||[-0.2,-0.1] || 0.1812 +/- 0.0025 || [[File:VyDiff--0.2,-0.1- 30DegRot.png|200px]] || *** || [0.1,0.2] || 0.136 +/- 0.003 || [[File:VyDiff-0.1,0.2- 30DegRot.png|200px]]
+
||Z = (-3.0 cm, -2.5 cm)
 
|-
 
|-
−
||[-0.1,0.0] || 0.1503 +/- 0.0021 || [[File:VyDiff--0.1,0.0- 30DegRot.png|200px]] || *** || [0.0,0.1] || 0.2052 +/- 0.0033  || [[File:VyDiff-0.0,0.1- 30DegRot.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
 +
||Sigma (cm) || 0.1339 +/- 0.0065 || 0.1539 +/- 0.0038 || 0.202 +/- 0.004 || 0.2537 +/- 0.0061 || 0.2517 +/- 0.0062
 
|}<br>
 
|}<br>
  
 +
It would seem that the bimodal distribution is having an effect on the results. It is counterintuitive that the resolution would get better the farther away from zero the events are. To begin investigating this, I made a Radius vs. Sigma plot for several values of Z. Here are some sample command lines in ROOT to get the width of the Gaussian peak.
  
−
Below are the histograms for a 2cm Y target with an incident electron energy of 6 GeV. The angles were theta = 25 degrees and phi = 210 degrees
+
 
 +
clas12->Draw("Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<1.0 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.8 && GenPart.z = 0");
 +
 
 +
clas12->Draw("GenPart.z - Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.6 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.4 && GenPart.z > 0.1 && GenPart.z < 0.5");
 +
 
 +
clas12->Draw("GenPart.z - Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.6 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.4 && GenPart.z > 0.5 && GenPart.z < 1.0");
 +
 
 +
 
 +
 
 +
 
 +
[[File:Radius vs Sigma Bimodal Investigation.png|200px]]
  
  
 
{|border="5"
 
{|border="5"
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
 
|-
 
|-
−
|| [[ File:GenPart.x YTarg 210DegRot.png|200px]] || [[File:GenPart.y YTarg 210DegRot.png|200px]] || [[File:GenPart.z YTarg 210DegRot.png|200px]]  || [[ File:Event.x YTarg 210DegRot.png|200px]] || [[File:Event.y YTarg 210DegRot.png|200px]] || [[ File:Event.z YTarg 210DegRot.png|200px]]
+
|| Z = 0.0 cm
−
|-
 
−
|}<br>
 
−
 
 
−
{|border="5"
 
−
||Interval || Resolution (cm) || Vy Difference || *** || Interval || Resolution (cm) || Vy Difference
 
 
|-
 
|-
−
||[-1.0,-0.9] || 0.04815 +/- 0.00067 || [[File:VyDiff--1.0,-0.9- YTarg 210DegRot.png|200px]] || *** || [0.9,1.0] || 0.07184 +/- 0.00181 || [[File:VyDiff-0.9,1.0- YTarg 210DegRot.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
−
||[-0.9,-0.8] || 0.05734 +/- 0.00091 || [[File:VyDiff--0.9,-0.8- YTarg 210DegRot.png|200px]] || *** || [0.8,0.9] || 0.08837 +/- 0.00268 || [[File:VyDiff-0.8,0.9- YTarg 210DegRot.png|200px]]
+
||Sigma (cm) || 0.2873 +/- 0.0035 || 0.3457 +/- 0.0026 || 0.4045 +/- 0.0026 || 0.4466 +/- 0.0026 || 0.5359 +/- 0.0033
 
|-
 
|-
−
||[-0.8,-0.7] || 0.05873 +/- 0.00085 || [[File:VyDiff--0.8,-0.7- YTarg 210DegRot.png|200px]] || *** || [0.7,0.8] || 0.0982 +/- 0.0024 || [[File:VyDiff-0.7,0.8- YTarg 210DegRot.png|200px]]
+
||*******************************************
 
|-
 
|-
−
||[-0.7,-0.6] || 0.05868 +/- 0.00089 || [[File:VyDiff--0.7,-0.6- YTarg 210DegRot.png|200px]] || *** || [0.6,0.7] || 0.09622 +/- 0.00305 || [[ File:VyDiff-0.6,0.7- YTarg 210DegRot.png|200px]]
+
|| Z = (0.1 cm, 0.5 cm)
 
|-
 
|-
−
||[-0.6,-0.5] || 0.05962 +/- 0.00098 || [[File:VyDiff--0.6,-0.5- YTarg 210DegRot.png|200px]] || *** || [0.5,0.6] || 0.08028 +/- 0.00156 || [[File:VyDiff-0.5,0.6- YTarg 210DegRot.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
−
||[-0.5,-0.4] || 0.0645 +/- 0.0014 || [[File:VyDiff--0.5,-0.4- YTarg 210DegRot.png|200px]] || *** || [0.4,0.5] || 0.07917 +/- 0.00163 || [[File:VyDiff-0.4,0.5- YTarg 210DegRot.png|200px]]
+
||Sigma (cm) || 0.141 +/- 0.010 || 0.1651 +/- 0.0086 || 0.1991 +/- 0.0082 || 0.2572 +/- 0.0093 || 0.2676 +/- 0.0081
 
|-
 
|-
−
||[-0.4,-0.3] || 0.0861 +/- 0.0020 || [[File:VyDiff--0.4,-0.3- YTarg 210DegRot.png|200px]] || *** || [0.3,0.4] || 0.08056 +/- 0.00159 || [[File:VyDiff-0.3,0.4- YTarg 210DegRot.png|200px]]
+
||*******************************************
 
|-
 
|-
−
||[-0.3,-0.2] || 0.1003 +/- 0.0024 || [[File:VyDiff--0.3,-0.2- YTarg 210DegRot.png|200px]] || *** || [0.2,0.3] || 0.08939 +/- 0.00201 || [[ File:VyDiff-0.2,0.3- YTarg 210DegRot.png|200px]]
+
||Z = (0.5 cm, 1.0 cm)
 
|-
 
|-
−
||[-0.2,-0.1] || 0.1305 +/- 0.0024 || [[File:VyDiff--0.2,-0.1- YTarg 210DegRot.png|200px]] || *** || [0.1,0.2] || 0.186 +/- 0.003 || [[File:VyDiff-0.1,0.2- YTarg 210DegRot.png|200px]]
+
||R (cm) || 0.1 || 0.3 || 0.5 || 0.7 || 0.9
 
|-
 
|-
−
||[-0.1,0.0] || 0.2042 +/- 0.0033 || [[ File:VyDiff--0.1,0.0- YTarg 210DegRot.png|200px]] || *** || [0.0,0.1] || 0.1476 +/- 0.0021  || [[File:VyDiff-0.0,0.1- YTarg 210DegRot.png|200px]]
+
||Sigma (cm) || 0.1672 +/- 0.0109 || 0.1636 +/- 0.0064 || 0.2277 +/- 0.0075 || 0.3203 +/- 0.0107 || 0.3287 +/- 0.0082
 
|-
 
|-
 
|}<br>
 
|}<br>
  
−
=== Localized Vertex Resolution Investigation of 2 Dimensional Targets ===
 
−
The histograms below were created using a 6 GeV electron fired at 25 degrees in theta and 30 degrees in phi. To make the cuts I simply made circles of increasing radius centered at the origin. I used 0.1cm increments to make the 10 histograms for each vertex position.
 
  
−
Below are the Vx and Vy Differences for a 2cm XY target, Z=0.
+
To investigate the mystery as to why the resolution seems to get better as we move away from Z = 0 cm, I will plot create radius vs. sigma plots for different values of Z to try and pinpoint the problem.
 +
 
 +
Below is a link to the histograms for Z = 0 cm. A sample command line used is shown.
 +
 
 +
root [5] clas12->Draw("GenPart.z - Event.z >> (120,-6,6)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.1 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.0 && GenPart.z = 0");
 +
 
 +
[[Histograms for Increasing Radii, Z = 0cm]]
 +
 
 +
[[File:Radius vs Sig GenPart.z=0.png|200px]]
 +
 
 +
Now that the Z = 0cm case has been done, the annular cuts will start to have a thickness of 0.25 cm in the Z direction. A sample command line in root is provided below. Notice that the annular thickness has been increased from 0.05 cm to 0.1 cm to increase the number of events in each histogram.
 +
 
 +
 
 +
root [5] clas12->Draw("GenPart.z - Event.z >> (120,-6,6)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.05 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.0 && GenPart.z > 0 && GenPart.z < 0.25");
  
−
{|border="5"
+
[[Histograms for Increasing Radii, Z = (0.0cm,0.25cm)]]
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
−
|-
 
−
|| [[ File:GenPart.x XYTarg 30DegRot.png|200px]] || [[File:GenPart.y XYTarg 30DegRot.png|200px]] || [[File:GenPart.z XYTarg 30DegRot.png|200px]] || [[File:Event.x XYTarg 30DegRot.png|200px]] || [[File:Event.y XYTarg 30DegRot.png|200px]] || [[File:Event.z XYTarg 30DegRot.png|200px]]  
 
−
|-
 
−
|}<br>
 
  
−
{|border="5"
+
It would seem that the resolution when 0.6cm<R<0.7cm has failed completely. To double check on lds3 go to
−
||Radius (cm)|| Resolution (cm) || Vx Difference || *** || Radius (cm) || Resolution (cm) || Vx Difference
 
−
|-
 
−
|| 0.1 || 0.2309 +/- 0.0091 ||[[File:VxDiff R=0.1 XYTarg 30DegRot.png|200px]] || *** || 0.6 || 0.259 +/- 0.001 || [[File:VxDiff R=0.6 XYTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.2 || 0.235 +/- 0.004 ||[[File:VxDiff R=0.2 XYTarg 30DegRot.png|200px]] || *** || 0.7 || 0.2769 +/- 0.0014 || [[File:VxDiff R=0.7 XYTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.3 || 0.2242 +/- 0.0028 || [[File:VxDiff R=0.3 XYTarg 30.png|200px]] || *** || 0.8 || 0.2927 +/- 0.0013 || [[File:VxDiff R=0.8 XYTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.4 || 0.2272 +/- 0.0020 || [[File:VxDiff R=0.4 XYTarg 30DegRot.png|200px]] || *** || 0.9 || 0.3074 +/- 0.0013 || [[File:VxDiff R=0.9 XYTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.5 || 0.2422 +/- 0.0016 || [[File:VxDiff R=0.5 XYTarg 30DegRot.png|200px]] || *** ||1.0|| 0.3237 +/- 0.0014 || [[ File:VxDiff R=1.0 XYTarg 30DegRot.png|200px]]
 
−
|}<br>
 
  
−
{|border="5"
+
/home/lds/src/CLAS/GEMC/experiments/eg12/vertex/XYZRaster/Solenoid_On/30DegRot
−
||Radius (cm)|| Resolution (cm) || VyDifference || *** || Radius (cm) || Resolution (cm) || Vy Difference
 
−
|-
 
−
|| 0.1 || 0.162 +/- 0.006 || [[ File:VyDiff R=0.1 XYTarg 30DegRot.png|200px]]|| *** || 0.6 || 0.1733 +/- 0.0020 || [[ File:VyDiff R=0.6 XYTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.2 || 0.1798 +/- 0.0031 || [[File:VyDiff R=0.2 XYTarg 30DegRot.png|200px]] || *** || 0.7 || 0.1661 +/- 0.0017 || [[File:VyDiff R=0.7 XYTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.3 || 0.1947 +/- 0.0028 || [[File:VyDiff R=0.3 XYTarg 30DegRot.png|200px]] || *** || 0.8 || 0.1615 +/- 0.0015 || [[File:VyDiff R=0.8 XYTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.4 || 0.1959 +/- 0.0033 || [[File:VyDiff R=0.4 XYTarg 30DegRot.png|200px]] || *** || 0.9 || 0.1578 +/- 0.0013 || [[File:VyDiff R=0.9 XYTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.5 || 0.1861 +/- 0.0027 || [[File:VyDiff R=0.5 XYTarg 30DegRot.png|200px]] || *** ||1.0|| 0.4832 +/- 0.0035 || [[ File:VyDiff R=1.0 XYTarg 30DegRot.png|200px]]
 
−
|}<br>
 
  
−
Below are the Vy and Vz differences for a 2cm target in Y and Z, X=0. The electrons were fired with an energy of 6 GeV and angles of 25 degrees in theta and 30 degrees in phi.
+
root -l eg12_sol_75k_2cm_XYRaster_6cm_ZRaster_30DegRot_rec_cat.root
  
 +
then use the command
  
−
{|border="5"
+
clas12->Draw("GenPart.z - Event.z>>(120,-6,6)","sqrt(GenPart.x*GenPart.x + GenPart.y*GenPart.y)>0.60 && sqrt(GenPart.x*GenPart.x + GenPart.y*GenPart.y)<0.70 && GenPart.z > 0.0 && GenPart.z<0.25");
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z  
 
−
|-
 
−
|| [[ File:GenPart.x 2cmYZTarg 30DegRot.png|200px]] || [[File:GenPart.y 2cmYZTarg 30DegRot.png|200px]] || [[File:GenPart.z 2cmYZTarg 30DegRot.png|200px]] || [[File:Event.x 2cmYZTarg 30DegRot.png|200px]] || [[File:Event.y 2cmYZTarg 30DegRot.png|200px]] || [[File:Event.z 2cmYZTarg 30DegRot.png|200px]]
 
−
|-
 
−
|}<br>
 
  
−
{|border="5"
+
Then by doing a Gaussian fit, the problem will appear.
−
||Radius (cm)|| Resolution (cm) || Vy Difference || *** || Radius (cm) || Resolution (cm) || Vy Difference
 
−
|-
 
−
|| 0.1 || 0.1722 +/- 0.0065 || [[File:VyDiff R=0.1 YZTarg 30DegRot.png|200px]] || *** || 0.6 || 0.1806 +/- 0.0017 || [[File:VyDiff R=0.6 YZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.2 || 0.1773 +/- 0.0037 || [[File:VyDiff R=0.2 YZTarg 30DegRot.png|200px]] || *** || 0.7 || 0.1868 +/- 0.0015 || [[ File:VyDiff R=0.7 YZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.3 || 0.1781 +/- 0.0031 || [[File:VyDiff R=0.3 YZTarg 30DegRot.png|200px]] || *** || 0.8 || 0.1974 +/- 0.0014 || [[File:VyDiff R=0.8 YZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.4 || 0.1734 +/- 0.0024 || [[File:VyDiff R=0.4 YZTarg 30DegRot.png|200px]] || *** || 0.9 || 0.2028 +/- 0.0013 || [[File:VyDiff R=0.9 YZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.5 || 0.1764 +/- 0.0020 || [[File:VyDiff R=0.5 YZTarg 30DegRot.png|200px]] || *** ||1.0|| 0.221 +/- 0.001 || [[File:VyDiff R=1.0 YZTarg 30DegRot.png|200px]]
 
−
|}<br>
 
  
−
{|border="5"
+
[[Histograms for Increasing Radii, Z = (0.0cm,0.25cm)]]
−
||Radius (cm)|| Resolution (cm) || Vz Difference || *** || Radius (cm) || Resolution (cm) || Vz Difference
 
−
|-
 
−
|| 0.1 || 0.07095 +/- 0.00239 || [[File:VzDiff R=0.1 YZTarg 30DegRot.png|200px]] || *** || 0.6 || 0.261 +/- 0.001 || [[File:VzDiff R=0.6 YZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.2 || 0.1063 +/- 0.0015 || [[File:VzDiff R=0.2 YZTarg 30DegRot.png|200px]] || *** || 0.7 || 0.2874 +/- 0.0010 || [[File:VzDiff R=0.7 YZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.3 || 0.146 +/- 0.001 || [[File:VzDiff R=0.3 YZTarg 30DegRot.png|200px]] || *** || 0.8 || 0.3232 +/- 0.0011 || [[File:VzDiff R=0.8 YZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.4 || 0.1833 +/- 0.0012 || [[File:VzDiff R=0.4 YZTarg 30DegRot.png|200px]] || *** || 0.9 || 0.3528 +/- 0.0010 || [[File:VzDiff R=0.9 YZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.5 || 0.2222 +/- 0.0012 || [[File:VzDiff R=0.5 YZTarg 30DegRot.png|200px]] || *** ||1.0|| 0.3847 +/- 0.0010 || [[File:VzDiff R=1.0 YZTarg 30DegRot.png|200px]]  
 
−
|}<br>
 
  
−
Below are the Vx and Vz differences for a 2cm XZ target, Y = 0. The electrons were fired with an energy of 6 GeV at angles theta = 25 degrees and phi = 30 degrees.
+
[[Histograms for Increasing Radii, Z = (0.25cm,0.5cm)]]
  
 +
[[Histograms for Increasing Radii, Z = (0.5cm,0.75cm)]]
  
−
{|border="5"
+
[[Histograms for Increasing Radii, Z = (0.75cm,1.0cm)]]
−
|| GenPart.x || GenPart.y || GenPart.z || Event.x || Event.y || Event.z
 
−
|-
 
−
|| [[File:GenPart.x 2cmXZTarg 30DegRot.png|200px]] || [[File:GenPart.y 2cmXZTarg 30DegRot.png|200px]] || [[File:GenPart.z 2cmXZTarg 30DegRot.png|200px]] || [[File:Event.x 2cmXZTarg 30DegRot.png|200px]] || [[File:Event.y 2cmXZTarg 30DegRot.png|200px]] || [[File:Event.z 2cmXZTarg 30DegRot.png|200px]]
 
−
|-
 
−
|}<br>
 
  
−
{|border="5"
+
[[Histograms for Increasing Radii, Z = (1.0cm,1.25cm)]]
−
||Radius (cm)|| Resolution (cm) || Vz Difference || *** || Radius (cm) || Resolution (cm) || Vz Difference
 
−
|-
 
−
|| 0.1 || 0.06193 +/- 0.00199 || [[File:VzDiff R=0.1 XZTarg 30DegRot.png|200px]] || *** || 0.6 || 0.2495 +/- 0.0012 || [[File:VzDiff R=0.6 XZTarg 30DegRot.png|200px]] 
 
−
|-
 
−
||0.2 || 0.1059 +/- 0.0015 || [[File:VzDiff R=0.2 XZTarg 30DegRot.png|200px]] || *** || 0.7 || 0.2862 +/- 0.0011 || [[File:VzDiff R=0.7 XZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.3 || 0.1412 +/- 0.0013 || [[File:VzDiff R=0.3 XZTarg 30DegRot.png|200px]] || *** || 0.8 || 0.3172 +/- 0.001 || [[File:VzDiff R=0.8 XZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.4 || 0.1704 +/- 0.0012 || [[File:VzDiff R=0.4 XZTarg 30DegRot.png|200px]] || *** || 0.9 || 0.3512 +/- 0.0012 || [[File:VzDiff R=0.9 XZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.5 || 0.2183 +/- 0.0013 || [[File:VzDiff R=0.5 XZTarg 30DegRot.png|200px]] || *** ||1.0|| 0.4066 +/- 0.0013 || [[File:VzDiff R=1.0 XZTarg 30DegRot.png|200px]]  
 
−
|}<br>
 
  
 +
[[Histograms for Increasing Radii, Z = (1.25cm,1.5cm)]]
  
−
{|border="5"
+
[[Histograms for Increasing Radii, Z = (1.5cm,1.75cm)]]
−
||Radius (cm)|| Resolution (cm) || Vx Difference || *** || Radius (cm) || Resolution (cm) || Vx Difference
 
−
|-
 
−
|| 0.1 || 0.2125 +/- 0.0090 || [[File:VxDiff R=0.1 XZTarg 30DegRot.png|200px]] || *** || 0.6 || 0.2365 +/- 0.0016 || [[File:VxDiff R=0.6 XZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.2 || 0.2392 +/- 0.0044 || [[File:VxDiff R=0.2 XZTarg 30DegRot.png|200px]] || *** || 0.7 || 0.2307 +/- 0.0013 || [[File:VxDiff R=0.7 XZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.3 || 0.251 +/- 0.003 || [[ File:VxDiff R=0.3 XZTarg 30DegRot.png|200px]]|| *** || 0.8 || 0.2251 +/- 0.0012 || [[File:VxDiff R=0.8 XZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.4 || 0.2494 +/- 0.0023 || [[File:VxDiff R=0.4 XZTarg 30DegRot.png|200px]] || *** || 0.9 || 0.222 +/- 0.001 || [[File:VxDiff R=0.9 XZTarg 30DegRot.png|200px]]
 
−
|-
 
−
||0.5 || 0.2439 +/- 0.0019 || [[File:VxDiff R=0.5 XZTarg 30DegRot.png|200px]] || *** ||1.0|| 0.2193 +/- 0.0010 || [[ File:VxDiff R=1.0 XZTarg 30DegRot.png|200px]]
 
−
|}<br>
 
  
 +
[[Histograms for Increasing Radii, Z = (1.75cm,2.0cm)]]
  
−
===Localized Vertex Resolution of 3 Dimensional targets===
+
[[Histograms for Increasing Radii, Z = (2.0cm,2.25cm)]]
−
For the plots below, a 6 GeV electron was fired at angles 25 degrees in theta and 30 degrees in phi. The target has an XY radius of 1cm and a length in the Z direction of 6cm. Setting GenPart.z = 0cm, the resolution was investigated as a function of the target's XY radius along with a table for the values.
 
  
−
[[ File:TargetRadius vs Width Z=0.png|200px]]
+
[[Histograms for Increasing Radii, Z = (2.25cm,2.5cm)]]
  
−
clas12->Draw("Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.95 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.85");
+
[[Histograms for Increasing Radii, Z = (2.5cm,2.75cm)]]
  
−
{|border="5"
+
[[Histograms for Increasing Radii, Z = (2.75cm,3.0cm)]]
−
|-
 
−
||R (cm) || 0.1 || 0.2 || 0.3 || 0.4  ||0.5||0.6||0.7||0.8||0.9||1.0
 
−
|-
 
−
||Width (cm) ||0.068 +/-  0.002 || 0.073 +/- 0.001 ||  0.1764 +/- 2.6134 || 0.59  +/-  0.0082 || 0.74 +/-    0.009 || 0.785 +/- 0.004 || 0.8713 +/- 0.0043 || 1.003 +/- 0.005 || 1.26 +/-    0.012
 
−
|-
 
−
|}<br> 
 
  
−
Here is the Radius vs Width plot for when abs(GenPart.z) <= 0.5cm along with a table of values.
+
In the histograms for increasing radii for Z = (-0.25cm,0.0cm) (not here yet), the histogram for 0.4cm<R<0.5cm seems very odd, but I verified it with root. Do a gaussian fit with the file eg12_sol_75k_2cm_XYRaster_6cm_ZRaster_30DegRot_rec_cat.root
  
−
[[File:Radius vs Width Z=1 30DegRot.png|200px]]
+
and use the command line
  
−
{|border="5"
+
root [1] clas12->Draw("GenPart.z - Event.z>>(120,-6,6)","sqrt(GenPart.x*GenPart.x + GenPart.y*GenPart.y)>0.4 && sqrt(GenPart.x*GenPart.x + GenPart.y*GenPart.y)<0.5 && GenPart.z > -0.25 && GenPart.z<0.0");
−
|-
 
−
||R (cm) || 0.1 || 0.2 || 0.3 ||  0.4 ||0.5||0.6||0.7||0.8||0.9||1.0
 
−
|-
 
−
||Width (cm) || 0.345 +/- 0.032 || 0.2889 +/- 0.0101 || 0.2704 +/- 0.0053 ||  || 0.2821 +/- 0.0042 || 0.2782 +/- 0.0035 || 0.287 +/- 0.003 || 0.294 +/- 0.003 || 0.294 +/- 0.003 || 0.2967 +/- 0.003
 
−
|-
 
−
|}<br>
 
  
−
Here is the Radius vs Width plot for when abs(GenPart.z) <= 1.0 cm along with a table of values.
 
−
 
−
[[File:Radius vs width z=2cm.png|200px]]
 
  
−
{|border="5"
+
Below are the plots of the Annular Radius vs. Sigma for the negative half of the target.
−
|-
 
−
||R (cm) || 0.1 || 0.2 || 0.3 || 0.4 || 0.4 ||0.5||0.6||0.7||0.8||0.9||1.0
 
−
|-
 
−
||Width (cm) || 0.5467 +/- 0.0351 || 0.4475 +/- 0.0102 || 0.4976 +/- 0.0084 || 0.505 +/- 0.006 || 0.4966 +/- 0.0055 || 0.4884 +/- 0.0045 || 0.502 +/- 0.004 || 0.5033 +/- 0.0038 || 0.4788 +/- 0.0029 || 0.4766 +/- 0.0026
 
−
|-
 
−
|}<br>
 
  
 +
[[File:AnnularRad vs Sigma Z=(-1.0,0.0).png|200px]]
 +
[[File:AnnularRad vs Sigma Z=(-2.0,-1.0).png|200px]]
 +
[[File:AnnularRad vs Sigma Z=-3.0,-2.0.png|200px]]
  
−
For this section I created a target that is 2cm in X and Y, and 6cm in Z. To produce the histograms I made a cut in the radius of a cylinder (R=0.1cm, R=0.2cm, .... , R=1.0cm) and also cut Z (Z=1cm, Z=2cm,...,Z=6cm) so that for each fixed radius there will be 6 histograms corresponding to changes in Z. For example, assume I am using R=0.1cm. There will be 6 histograms for X,Y,and Z corresponding to changing Z from 1cm to 6cm in 1cm increments. I also placed a cut for the reconstructed events using the commands abs(Event.z) <= 4.0 and sqrt(Event.x*Event.x+Event.y*Event.y) <=1.
+
Here are the histograms for the positive half of the target
  
−
For the plots below, a 6 GeV electron was fired at angles 25 degrees in theta and 30 degrees in phi. The target has an XY radius of 1cm and a length in the Z direction of 6cm. Setting GenPart.z = 0cm, the resolution was investigated as a function of the target's XY radius along with a table for the values.
+
[[File:AnnularRad vs sigma Z=0.0,1.0.png|200px]]
 +
[[File:Rad vs Sigma z=1.0,2.0.png|200px]]
 +
[[File:Rad vs Sigma Z=2.0,3.0.png|200px]]
  
 +
Now using GEMC 2.5 I will attempt to recreate the plots as seen in the JLAB wiki created by Dr. Forest.
  
−
Below are the Vx Differences for R=1.0cm as an example.
+
[[Recreation of Plots Using GEMC 2.5]]
  
−
{|border="5"
+
[[Investigation of Centroid Shift in Vz Differences]]
−
||Z (cm)|| Resolution (cm) || Vx Difference || *** || Z (cm) || Resolution (cm) || Vx Difference
 
−
|-
 
−
|| 1.0 || 0.305 +/- 0.003 || [[File:VxDiff R=1.0 Z=1 30DegRot.png.png|200px]] || *** || 4.0 || 0.3459 +/- 0.0018 || [[ File:VxDiff R=1.0 Z=4 30DegRot.png|200px]]
 
−
|-
 
−
||2.0 || 0.307 +/- 0.003 || [[File:VxDiff R=1.0 z=2 30DegRot.png|200px]] || *** || 5.0 || 0.3688 +/- 0.0016 || [[File:VxDiff R=1.0 Z=5 30DegRot.png|200px]] 
 
−
|-
 
−
||3.0 || 0.3214 +/- 0.0021 || [[File:VxDiff R=1.0 Z=3 30DegRot.png|200px]] || *** || 6.0 || 0.3877 +/- 0.0015 || [[File:VxDiff R=1.0 Z=6 30DegRot.png|200px]]
 
−
|}<br>
 
  
 
=Elastic electron proton GEMC 2.4 & Coatjava 2.4=
 
=Elastic electron proton GEMC 2.4 & Coatjava 2.4=

Latest revision as of 16:39, 11 November 2016

Vertex Reconstruction studies

Inclusive electron GEMC 2.4 & Coatjava 2.4

LB_GEMC2.4CJ2.4_Vertex

Phi angle gcard vs. LUND


Summary

Set all histogram ranges to -6,6 cm  and bin sizes of 0.1 cm

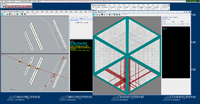
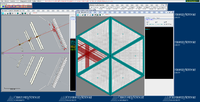
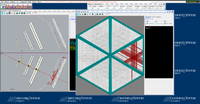
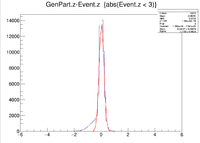
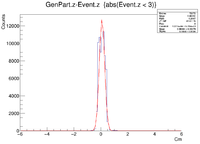
Below are some of the sample GEMC simulations as seen in the CED


6cm Z Target, No Rotation 6cm Z Target, 270 Degree Rotation 6cm Z Target, 90 Degree Rotation 2cm Y Target, 30 Degree Rotation 2cm Y Target, 180 Degree Rotation 2cm X Target, 90 Degree Rotation 2cm X Target, 270 Degree Rotation
Ced ZRaster 0DegRot.png 6cm ZTarg 270DegRot CED.png Ced ZRaster 90DegRot.png 2cm YRaster 30DegRot ced.png Ced YRaster 180DegRot.png Ced XRaster 90DegRot.png Ced XRaster 270DegRot.png


There is a bash script on lds2 that will create Vx,Vy, and Vz differences for a point target, 3 2 cm line targets (in X,Y, and Z), 2 2D targets (one XZ target where X = 2cm and Z = 6cm and another where Y = 2cm and Z = 6 cm), and one 3D target where X = Y = 2cm and Z = 6cm. A 6 GeV electron is fired at angles [math]\theta = 25[/math] degrees and [math]\phi = 30[/math] degrees. The path to the script is /home/lds/src/CLAS/GEMC/experiments/eg12/vertex and the file is called run.exe. To run it you must be in a tcsh and have the setup in the GEMC directory sourced. Then simply hit ./run.exe. Right now the number of events is small (100), but that can easily be changed within the script.

Point target X,Y,Z=0 cm

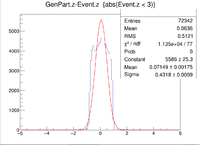
The histograms below are using a 6 GeV electron fired at an angles of 25 degrees in theta and 0 degrees in phi.

For the plots below, I used the following gcard, sample LUND file, and commands in GEMC 2.4, coat-java 2.4, and ROOT

gcard:

<gcard> 

      <detector name="../../../../clas12/fc/forwardCarriage" factory="TEXT" variation="original"/>
      <detector name="../../../../clas12/dc/dc"            factory="TEXT" variation="ccdb"/>
      <detector name="../../../../clas12/ec/ec"            factory="TEXT" variation="original"/>
      <detector name="../../../../clas12/ctof/ctof"            factory="TEXT" variation="original"/>
      <detector name="../../../../clas12/ftof/ftof"            factory="TEXT" variation="java"/>
      <detector name="../../../../clas12/htcc/htcc"            factory="TEXT" variation="original"/>
      <detector name="../../../../clas12/pcal/pcal"            factory="TEXT" variation="javageom"/>
      <detector name="../../../../clas12/magnets/solenoid" factory="TEXT" variation="original"/>
      <option name="SCALE_FIELD" value="clas12-torus-big, -1"/>
      <option name="HALL_FIELD"  value="clas12-solenoid"/>
      <option name="OUTPUT" value="evio,eg12_sol_75k_No_Raster.ev"/>

</gcard>

Sample LUND File:

1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 0 0 0 1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 0 0 0 1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 0 0 0


GEMC Command:

~/src/CLAS/GEMC/source/gemc -USE_GUI=0 -INPUT_GEN_FILE="LUND,No_Raster.LUND" -N=75000 eg12_sol_No_Raster.gcard

Coat-Java 2.4 command:

~/src/CLAS/coatjava-2.4/bin/clas12-reconstruction -i ../files/vertex/vertex.evio -config GEOM::new=true -config MAG::torus=-1.0 -config MAG::solenoid=1.0 -o ../files/vertex/vertex_rec.evio -s DCHB:DCTB:EC:FTOF:EB -config DATA::mc=true -config DCTB::useRaster=true

Sample ROOT command:

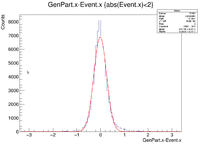
clas12->Draw("GenPart.x - Event.x","abs(Event.x)<3");


No Rastering
Vx Difference 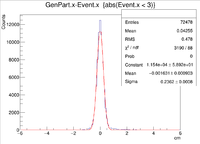NoRaster VxDifference sol.png
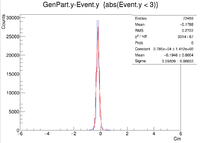
Vy Difference NoRaster VyDifference sol.png
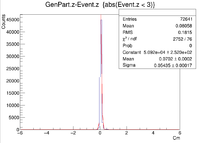
Vz Difference NoRaster VzDifference sol.png
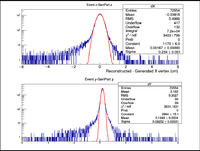
X Resolution (cm) 0.2362 +/- 0.0008
Y Resolution(cm) 0.09809 +/- 0.00033
Z Resolution (cm) 0.05435 +/- 0.00017


These histograms raise some questions. To begin I created a LUND file with 6 GeV incident electrons at 25 degrees in theta and 0 degrees in phi. All of the vertex positions were set to 0. I then ran GEMC 2.4 using the command line ~/src/CLAS/GEMC/source/gemc -USE_GUI=0 -INPUT_GEN_FILE="LUND,No_Raster.LUND" -N=75000 eg12_sol_No_Raster.gcard

which created an output file called eg12_sol_75k_No_Raster.ev. After that the reconstruction command line used was

~/src/CLAS/coatjava-2.4/bin/clas12-reconstruction -i eg12_sol_75k_No_Raster.ev-config GEOM::new=true -config MAG::torus=-1.0 -config MAG::solenoid=1.0 -o eg12_sol_75k_No_Raster_rec.evio -s DCHB:DCTB:EC:FTOF:EB -config DATA::mc=true -config DCTB::useRaster=true

After the reconstruction a root file was created using

~/src/CLAS/evio2root/bin/evio2root eg12_sol_75k_No_Raster_rec.evio eg12_sol_75k_No_Raster_rec.root 75000

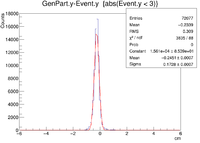
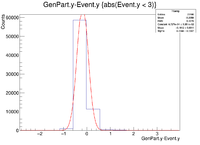
A plot was then created to show the X Vertex and Y Vertex Differences

NoRaster Vx YDifference.png

The first question is why is there a shift in the Y Difference. What would make X more centered around 0? The next question is when rastering begins, why do the resolutions in the X Vertices remain unchanged while the resolutions in the Y Vertices change?

Point in 2-D but extended target in 1-D

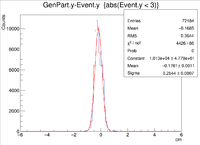
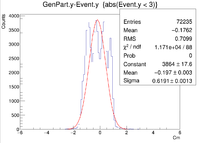
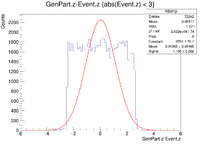
Two vertex variables are fixed at zero and the third vertex variable is altered. A 6 GeV electron was fired at angles of 25 degrees in theta and 0 degrees in phi.

The gcard used had the same detector parts as above, but the filename and pathways were changed.

Below is a sample line from the LUND files:

For 2cm X Target: 1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 0.999484 0 0

For 2cm Y Target: 1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 0 0.999484 0

For 2cm Z Target: 1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 0 0 2.99845


Also, here are the GEMC, Coat-Java, and a sample ROOT command.

GEMC: ~/src/CLAS/GEMC/source/gemc -USE_GUI=0 -INPUT_GEN_FILE="LUND,test.LUND" -N=100 eg12.gcard

Coat-Java:~/src/CLAS/coatjava-2.4/bin/clas12-reconstruction -i ../files/vertex/vertex.evio -config GEOM::new=true -config MAG::torus=-1.0 -config MAG::solenoid=1.0 -o ../files/vertex/vertex_rec.evio -s DCHB:DCTB:EC:FTOF:EB -config DATA::mc=true -config DCTB::useRaster=true

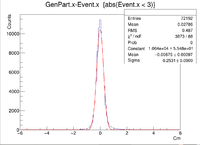
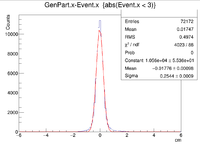
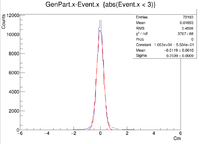
Sample ROOT command: clas12->Draw("GenPart.x - Event.x","abs(Event.x)<2");

2cm X Raster, Y=0,Z=0 2 cm Y Raster, X=0,Z=0 2 cm Z Raster ,X=0,Y=0 6 cm Z Raster ,X=0,Y=0
Vx Difference 1cm XRaster VxDifference sol 75k.png 1cm YRaster VxDifference sol.png 2cm ZRaster VxDifference sol.png 3cm ZRaster VxDifference sol.png
Vy Difference 1cm XRaster VyDifference sol.png YRaster Eventy.png 2cm ZRaster VyDifference sol.png 3cm ZRaster VyDifference sol.png
Vz Difference 1cm XRaster VzDifference sol.png 1cm YRaster VzDifference sol.png 2cm ZRaster VzDifference.png 3cm ZRaster VZDifference sol 75k.png
X Resolution (cm) 0.2658 +/- 0.0010 0.2531 +/- 0.0009 0.2544 +/- 0.0009 0.2539 +/- 0.0009
Y Resolution(cm) 0.1728 +/- 0.0007 0.2368 +/- 0.0007 0.2644 +/- 0.0007 0.6191 +/- 0.0013
Z Resolution (cm) 0.1792 +/- 0.0006 0.1998 +/- 0.0004 0.4318 +/- 0.0009 1.105 +/- 0.002


Extended target -3 < Z < 3 cm

For the plots below a 6 GeV electron was fired at angles theta = 25 degrees and phi = 0 degrees. There were 3 separate simulations ran for when -3 cm < Z < 3 cm. The first was a 2-D target with -3 cm < Z < 3 cm and -1 cm < X < 1 cm and Y = 0 cm, while the second had the same values for Z, but instead -1 cm < Y < 1cm and X = 0 cm. The final set of plots was created using -3 cm < Z < 3 cm , -1 cm < X < 1 cm, and -1 cm < Y < 1 cm.

Below are some of the sample LUND files used.

For the XZ Target:

1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 -0.67418 0 2.99845 1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 0.894402 0 -1.30429

For the YZ Target:

1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 0 -0.67418 2.99845 1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 0 0.894402 -1.30429


For the XYZ Target:

1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 -0.67418 -0.434764 2.99845 1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 -0.536687 -0.0300528 2.68321 1 1 1 1 1 1.00029 0.0718059 0.937771 1.48222 0.789865 1 -1 1 11 0 0 0 2.53564 5.43788 6 0.000511 0.488611 0.0800873 2.74486


The GEMC and Coat-Java command lines are similar to the previously seen commands. The only things that changed were the LUND file names, and the ev/evio filenames. The command lines can be seen at the top of the histograms.

VertREC_9-22-16_table_3ltZgt-3

Extended target in Z. Vy shift analysis

All Histograms below were created by simply making the target longer along the Z axis. Each case uses vertex points for X and Y ranging from -1cm to 1cm

VertREC_9-22-16_table_3ltZgt-3_1gtRlt-1

Localized Vertex Resolution Investigation of Line Targets

GEMC was ran to create electrons being produced in a line along certain axes. These include three separate 2cm targets centered at (0,0,0) in the X, Y , and Z directions. The final target is a line along the Z axis centered at (0,0,0) that is 6cm long. The generated electrons were shot at 25 degrees in theta and 0 degrees in phi at an energy of 6GeV.

Here is an example of how the cuts were made. Consider the case of a 2cm line target in the Z direction centered at (0,0,0). Closed intervals begin at the end of the target and are 0.1cm long. So the first interval would be [-1.0,-0.9], then the next would be [-0.9, -0.8] and so on until the entire target is covered. The events in the EVENTHB bank were cut so that in any given interval there would be a margin of +/- 1cm from the end of the area of interest to remove any outliers that may cause the histograms to have long tails.



Below are the histograms for the 2cm line target in Y,X=0,Z=0. The electrons were fired with an energy of 6 GeV at 25 degrees in theta at 0 degrees in phi.

2cm YLineTarg 0 Degree Rotation 09/23/16

Below are the histograms for a 2cm target along the Y axis, X = 0 Z = 0. The electrons were fired with an energy of 6 GeV at 25 degrees in theta and 180 degrees in phi.

2cm YLineTarg 180 Degree Rotation 09/23/16

Below are the Histograms for a 2cm long target in the X Direction with a 6GeV electron fired at 25 degrees in theta and 90 degrees in phi

2cm XLineTarg 90 Degree Rotation 09/23/16

Below are the Vx Differences using a 2cm target in X with incident 6 GeV electrons at 25 degrees in theta and 270 degrees in phi


2cm XLineTarg 270 Degree Rotation 09/23/16


Below are the histograms for a 6cm target in the Z direction using a 6 GeV electron fired at 25 degrees in theta and 0 degrees in phi.


6cm ZLineTarg 0 Degree Rotation 09/23/16

Below are the histograms for a 6cm target in the Z direction using a 6 GeV electron fired at 25 degrees in theta and 90 degrees in phi.


6cm ZLineTarg 90 Degree Rotation 09/23/16


Below are the histograms for a 6 GeV electron fired at angles 25 degrees in theta and 270 degrees in phi. The target was 6cm in the Z direction.


6cm ZLineTarg 270 Degree Rotation 09/23/16


Below are the histograms for a 2cm target along the Y axis, X = 0 Z = 0. The electrons were fired with an energy of 6 GeV at 25 degrees in theta and 30 degrees in phi.

2cm YLineTarg 30 Degree Rotation 09/23/16


Below are the histograms for a 2cm Y target with an incident electron energy of 6 GeV. The angles were theta = 25 degrees and phi = 210 degrees


2cm YLineTarg 210 Degree Rotation 09/23/16

Localized Vertex Resolution Investigation of 2 Dimensional Targets

The histograms below were created using a 6 GeV electron fired at 25 degrees in theta and 30 degrees in phi. To make the cuts I simply made circles of increasing radius centered at the origin. I used 0.1cm increments to make the 10 histograms for each vertex position.

Below are the Vx and Vy Differences for a 2cm XY target, Z=0.

2cm XYTarg Z=0 Vx and Vy Differences 09/23/16

Below are the Vy and Vz differences for a 2cm target in Y and Z, X=0. The electrons were fired with an energy of 6 GeV and angles of 25 degrees in theta and 30 degrees in phi.


2cm YZTarg X=0 Vz and Vy Difference 09/23/16

Below are the Vx and Vz differences for a 2cm XZ target, Y = 0. The electrons were fired with an energy of 6 GeV at angles theta = 25 degrees and phi = 30 degrees.


2cm XZTarg Y=0 Vx and Vz Differences 09/23/16

Localized Vertex Resolution of 3 Dimensional targets

For the plots below, a 6 GeV electron was fired at angles 25 degrees in theta and 30 degrees in phi. The target has an XY radius of 1cm and a length in the Z direction of 6cm. Setting GenPart.z = 0cm, the resolution was investigated as a function of the target's XY radius along with a table for the values.

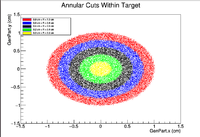
In this section, concentric rings with a thickness of 0.1cm were created within the target. For example these plots would include a ring centered at x=y=z=0 and include all GenPart.x and GenPart.y from (0.0 cm, 0.1 cm), then another ring would include all Genpart.x and GenPart.y events from (0.1 cm, 0.2 cm) and so on until we reach the edge of the target. Below is a visualization of the cuts as seen in a 2D cross section of the target.

2DTargAnnularCuts.png

AnnularRad vs Sigma z=0.png

clas12->Draw("Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.95 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.85");

R (cm) 0.05 +/- 0.05 0.15 +/- 0.05 0.25 +/- 0.05 0.35 +/- 0.05 0.45 +/- 0.05 0.55 +/- 0.05 0.65 +/- 0.05 0.75 +/- 0.05 0.85 +/- 0.05 0.95 +/- 0.05
Width (cm) 0.05094 +/- 0.0019 0.07812 +/- 0.0018 0.3688 +/- 0.0063 0.5231 +/- 0.0077 0.718 +/- 0.012 0.7987 +/- 0.0092 0.8709 +/- 0.0085 1.038 +/- 0.01 1.183 +/- 0.012 1.296 +/- 0.013


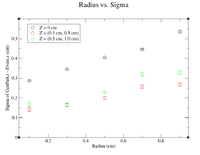
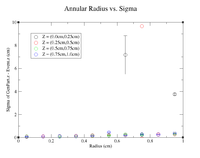
For the next set of plots, the GEMC simulations had the same energy and angles as above. To construct scatter plots, similar annular cuts in the radius were made (similar to above), but this time the thickness of each ring was 0.2 cm (to ensure enough events were present). In addition, the target will become extended in Z. Cuts were made in Z by restricting GenPart.z to be within a range of certain values. Each "washer" shape has a thickness of 0.5 cm in the Z direction. Histograms were created using the following command line as an example

clas12->Draw("GenPart.z - Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.2 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.0 && GenPart.z > 0.0 && GenPart.z < 0.5");


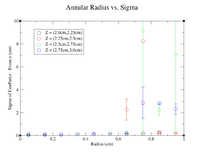
Below is a plot and a table for the Radius vs. Sigma of GenPart.z - Event.z for several cuts in Z. For the plot each Radius is centered at the point plotted with a width of +/- 0.1 cm.

Radius vs sigma pos half.png

Z = (0.0 cm, 0.5 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1548 +/- 0.0106 0.1825 +/- 0.0086 0.2167 +/- 0.0078 0.26 +/- 0.01 0.2774 +/- 0.0075
*******************************************
Z = (0.5 cm, 1.0 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1672 +/- 0.0109 0.1636 +/- 0.0064 0.2277 +/- 0.0075 0.3203 +/- 0.0107 0.3287 +/- 0.0082
*******************************************
Z = (1.0 cm, 1.5 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1282 +/- 0.0068 0.1551 +/- 0.0042 0.1842 +/- 0.0052 0.2172 +/- 0.0069 0.2587 +/- 0.0072
*******************************************
Z = (1.5 cm, 2.0 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1264 +/- 0.0071 0.1558 +/- 0.0042 0.1795 +/- 0.0043 0.2034 +/- 0.0049 0.2391 +/- 0.0055
*******************************************
Z = (2.0 cm, 2.5 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1723 +/- 0.0120 0.1519 +/- 0.0038 0.1896 +/- 0.0048 0.2033 +/- 0.0043 0.2361 +/- 0.0048
*******************************************
Z = (2.5 cm, 3.0 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1273 +/- 0.0054 0.1665 +/- 0.0057 0.1936 +/- 0.0041 0.2143 +/- 0.0042 0.2337 +/- 0.0050


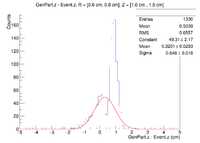
Here is where the problem of a bimodal distribution become relevant as seen below in the histogram.

GenPart.z - Event.z bimodal example.png

For now I will simply fit the larger peak to hopefully get rid of the muddling of the resolution, but this must be noted and investigated further later.

Below is the plot and the table for the negative half of the target.

Radius vs sigma neg half.png


Z = (-0.5 cm, 0.0 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1666 +/- 0.0128 0.1722 +/- 0.0078 0.1983 +/- 0.0067 0.2193 +/- 0.0060 0.2554 +/- 0.0068
*******************************************
Z = (-1.0 cm, -0.5 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1435 +/- 0.0069 0.1708 +/- 0.0068 0.2008 +/- 0.0069 0.2094 +/- 0.0058 0.2544 +/- 0.0065
*******************************************
Z = (-1.5 cm, -1.0 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1418 +/- 0.0073 0.1551 +/- 0.0047 0.2342 +/- 0.0092 0.2286 +/- 0.0066 0.2459 +/- 0.0066
*******************************************
Z = (-2.0 cm, -1.5 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1562 +/- 0.0091 0.1628 +/- 0.0045 0.2115 +/- 0.0076 0.2061 +/- 0.0056 0.2335 +/- 0.0077
*******************************************
Z = (-2.5 cm, -2.0 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1312 +/- 0.0059 0.1517 +/- 0.0040 0.2061 +/- 0.0049 0.257 +/- 0.008 0.2484 +/- 0.005
*******************************************
Z = (-3.0 cm, -2.5 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1339 +/- 0.0065 0.1539 +/- 0.0038 0.202 +/- 0.004 0.2537 +/- 0.0061 0.2517 +/- 0.0062


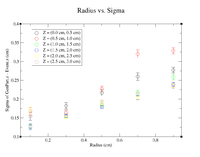
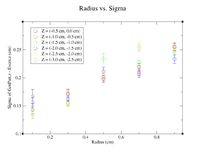
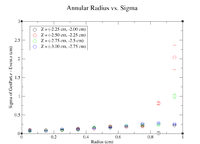
It would seem that the bimodal distribution is having an effect on the results. It is counterintuitive that the resolution would get better the farther away from zero the events are. To begin investigating this, I made a Radius vs. Sigma plot for several values of Z. Here are some sample command lines in ROOT to get the width of the Gaussian peak.


clas12->Draw("Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<1.0 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.8 && GenPart.z = 0");

clas12->Draw("GenPart.z - Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.6 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.4 && GenPart.z > 0.1 && GenPart.z < 0.5");

clas12->Draw("GenPart.z - Event.z >> (100,-5,5)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.6 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.4 && GenPart.z > 0.5 && GenPart.z < 1.0");



Radius vs Sigma Bimodal Investigation.png


Z = 0.0 cm
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.2873 +/- 0.0035 0.3457 +/- 0.0026 0.4045 +/- 0.0026 0.4466 +/- 0.0026 0.5359 +/- 0.0033
*******************************************
Z = (0.1 cm, 0.5 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.141 +/- 0.010 0.1651 +/- 0.0086 0.1991 +/- 0.0082 0.2572 +/- 0.0093 0.2676 +/- 0.0081
*******************************************
Z = (0.5 cm, 1.0 cm)
R (cm) 0.1 0.3 0.5 0.7 0.9
Sigma (cm) 0.1672 +/- 0.0109 0.1636 +/- 0.0064 0.2277 +/- 0.0075 0.3203 +/- 0.0107 0.3287 +/- 0.0082



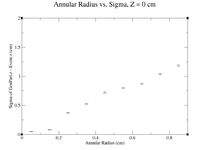
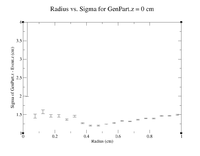
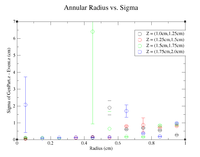
To investigate the mystery as to why the resolution seems to get better as we move away from Z = 0 cm, I will plot create radius vs. sigma plots for different values of Z to try and pinpoint the problem.

Below is a link to the histograms for Z = 0 cm. A sample command line used is shown.

root [5] clas12->Draw("GenPart.z - Event.z >> (120,-6,6)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.1 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.0 && GenPart.z = 0");

Histograms for Increasing Radii, Z = 0cm

Radius vs Sig GenPart.z=0.png

Now that the Z = 0cm case has been done, the annular cuts will start to have a thickness of 0.25 cm in the Z direction. A sample command line in root is provided below. Notice that the annular thickness has been increased from 0.05 cm to 0.1 cm to increase the number of events in each histogram.


root [5] clas12->Draw("GenPart.z - Event.z >> (120,-6,6)","sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)<0.05 && sqrt(GenPart.x*GenPart.x+GenPart.y*GenPart.y)>0.0 && GenPart.z > 0 && GenPart.z < 0.25");

Histograms for Increasing Radii, Z = (0.0cm,0.25cm)

It would seem that the resolution when 0.6cm<R<0.7cm has failed completely. To double check on lds3 go to

/home/lds/src/CLAS/GEMC/experiments/eg12/vertex/XYZRaster/Solenoid_On/30DegRot

root -l eg12_sol_75k_2cm_XYRaster_6cm_ZRaster_30DegRot_rec_cat.root

then use the command

clas12->Draw("GenPart.z - Event.z>>(120,-6,6)","sqrt(GenPart.x*GenPart.x + GenPart.y*GenPart.y)>0.60 && sqrt(GenPart.x*GenPart.x + GenPart.y*GenPart.y)<0.70 && GenPart.z > 0.0 && GenPart.z<0.25");

Then by doing a Gaussian fit, the problem will appear.

Histograms for Increasing Radii, Z = (0.0cm,0.25cm)

Histograms for Increasing Radii, Z = (0.25cm,0.5cm)

Histograms for Increasing Radii, Z = (0.5cm,0.75cm)

Histograms for Increasing Radii, Z = (0.75cm,1.0cm)

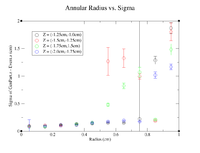
Histograms for Increasing Radii, Z = (1.0cm,1.25cm)

Histograms for Increasing Radii, Z = (1.25cm,1.5cm)

Histograms for Increasing Radii, Z = (1.5cm,1.75cm)

Histograms for Increasing Radii, Z = (1.75cm,2.0cm)

Histograms for Increasing Radii, Z = (2.0cm,2.25cm)

Histograms for Increasing Radii, Z = (2.25cm,2.5cm)

Histograms for Increasing Radii, Z = (2.5cm,2.75cm)

Histograms for Increasing Radii, Z = (2.75cm,3.0cm)

In the histograms for increasing radii for Z = (-0.25cm,0.0cm) (not here yet), the histogram for 0.4cm<R<0.5cm seems very odd, but I verified it with root. Do a gaussian fit with the file eg12_sol_75k_2cm_XYRaster_6cm_ZRaster_30DegRot_rec_cat.root

and use the command line

root [1] clas12->Draw("GenPart.z - Event.z>>(120,-6,6)","sqrt(GenPart.x*GenPart.x + GenPart.y*GenPart.y)>0.4 && sqrt(GenPart.x*GenPart.x + GenPart.y*GenPart.y)<0.5 && GenPart.z > -0.25 && GenPart.z<0.0");


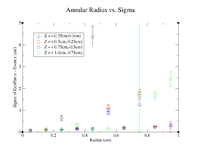
Below are the plots of the Annular Radius vs. Sigma for the negative half of the target.

AnnularRad vs Sigma Z=(-1.0,0.0).png AnnularRad vs Sigma Z=(-2.0,-1.0).png AnnularRad vs Sigma Z=-3.0,-2.0.png

Here are the histograms for the positive half of the target

AnnularRad vs sigma Z=0.0,1.0.png Rad vs Sigma z=1.0,2.0.png Rad vs Sigma Z=2.0,3.0.png

Now using GEMC 2.5 I will attempt to recreate the plots as seen in the JLAB wiki created by Dr. Forest.

Recreation of Plots Using GEMC 2.5

Investigation of Centroid Shift in Vz Differences

Elastic electron proton GEMC 2.4 & Coatjava 2.4

References

https://clasweb.jlab.org/wiki/index.php/TF_EG12_Vertex#Z_resolution_With_micro-megas

EG12#Vertex_Studies

Retrieved from "https://wiki.iac.isu.edu/index.php?title=LB_RunGroupC_Vertex&oldid=110074"