|
|
| (15 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | GEANT4 predicts that scattered electrons, photons, and positrons (mostly scattered electrons) deposit
| + | Niowave Positron Project Progress for November 2015 |
| | | | |
| − |
| |
| − | {| border="1"
| |
| − | | [[File:BeamPipeDepEmev_34.8_082915.png |200px]] || [[File:MCNPXBeamPipeDepEmev_34.8_090315.png |200px]]
| |
| − | |+ Energy deposited (MeV) in a 1 m long 3.48 cm diameter beam pipe surrounding a 2 mm target located at Z=-900 mm.
| |
| − | |}
| |
| − |
| |
| − | According to the above figure, GEANT4 predicts a total of <math>3.08\times 10^7</math> MeV (the integral adds up the energy in each 1cm bin) of energy will be deposited in
| |
| − | a 1m long beam pipe surrounding a 2 mm thick PbBi target located at Z=-902 mm when 20 million electrons impinge the target. The peak energy deposition is 0.3 MeV/e<math>^-</math>
| |
| − |
| |
| − | If this energy were uniformly distributed along the 5 mm thick beam pipe having a diameter of 3.48 cm then I would see
| |
| − |
| |
| − | :<math>3.08 \times 10^{10} \mbox{keV} \times \frac{1}{100 \mbox{cm}}\times \frac{1}{ \pi \times 3.48 \mbox {cm} } \times \frac{1}{2 \times 10^7 \mbox{e}^-}=3.5\frac{\mbox{keV}}{\mbox{cm}^2 \;\;\mbox{e}^-}</math>
| |
| | | | |
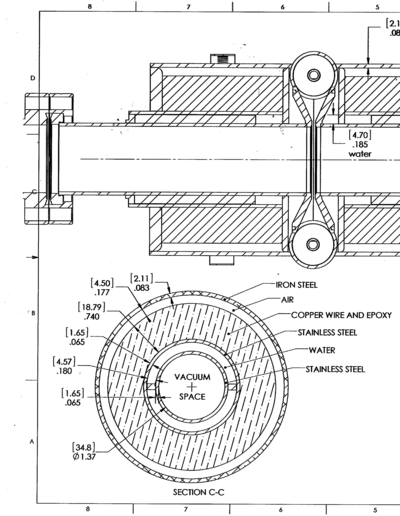
| | + | The next step in the positron project, after determining the PbBi thickness for maximum positron production, was to estimate the heat that would be deposited from the primary electron beam on the beam pipe. Electrons scattered by the PbBi target will intersect a beam pipe used to transport the desired positrons. Electrons traversing the beam pipe can deposit energy that will heat the beam pipe. The goal of this simulation was to estimate the amount of the deposited energy to determine if there is sufficient cooling to prevent a beam pipe breach. Below is a preliminary design of the beam pipe dimensions. |
| | | | |
| | | | |
| − | if you assume a 1 mA beam of electrons then this becomes
| |
| − |
| |
| − | <math>\left ( \frac{3.5 \; \mbox{W} }{ \mbox{cm}^2 } \right) </math>
| |
| − |
| |
| − | I converted the above histogram to deposited power by 1000 mA, divide by the number of incident electrons, divide by the circumference of the beam pipe, convert the number of electrons to Coulombs, and use a unit conversion from MeV to W-s per MeV.
| |
| − |
| |
| − | <math>\left(Counts \frac{\mbox{MeV}}{\mbox{cm}}\right) \times \left( \frac{1}{2 \times 10^{7} \mbox{e}^-} \right ) \times \left( \frac{1}{ \pi \times 3.48 \mbox{cm}} \right ) \times \left( \frac{1. \times 10^{-3}\mbox{ C}}{\mbox{s} }\right )\times \left( \frac{\mbox{e}^- }{1.6 \times 10^{-19}\mbox{ C}}\right ) \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right ) \times </math>
| |
| − |
| |
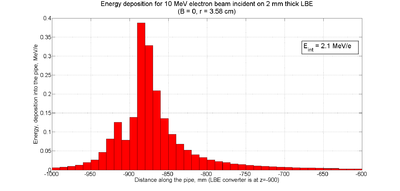
| − | If you use the above factors to weight the histogram, then the figure below shows that GEANT4 predicts a power deposition density of <math>= 4 \frac{W}{cm^2}</math>, 1 cm downstream of the target.
| |
| − | Back scattered electrons appear to create the hottest spot of <math>= 15 \frac{W}{cm^2}</math> about 1cm upstream of the target.
| |
| − |
| |
| | {| border="1" | | {| border="1" |
| − | | [[File:BeamPipeDepE_34.8mmA_082815.png| 200 px]] ||[[File:BeamPipeDepE_34.8mmB_082815.png| 200 px]]
| |
| | |- | | |- |
| − | | Power Deposition Zoomed in and 902 mm offset applied ||Power deposition over the 1 m long beam pipe | + | [[File:TF_Niowave_SolenoidDesign_9-3-15.png | 400 px]] |
| | |- | | |- |
| − | |} | + | |Element || dimension |
| − | | + | |- |
| − | | + | | Inner beam pipe radius || 1.74 cm |
| − | | + | |- |
| − | The energy deposited by electrons scattered into a 3.48 diameter stainless steel beam pipe (1.65 mm thick) from a PbBi target as a function of a uniform Solenoidal magnetic field.
| + | | Inner beam pipe thickness || 0.165 cm |
| − | | + | |- |
| − | | + | |water jacket thickness || 0.457 cm |
| − | {| border="1"
| |
| − | {| border="1"
| |
| − | | B-field (Tesla) || Hot Spot (<math>MeV/e^-</math>) | |
| | |- | | |- |
| − | | 0.0 || 0.35 | + | | outer beam pipe radius || 2.362 cm |
| − | |-
| |
| − | | 0.3 || 0.35
| |
| − | |-
| |
| − | | 1.0 || 0.35
| |
| − | |-
| |
| − | | 1.5 || 0.22
| |
| − | |-
| |
| − | | 2.0 || 0.10
| |
| − | |-
| |
| − | | 4.0 || 0.002
| |
| − | |+
| |
| − | |}
| |
| − | | |
| − | | |
| − | To convert this deposited energy per incident electron on the target to a heat load in the pipe you need to divide by the area of the pipe.
| |
| − | | |
| − | A histogram is filled with 1 cm bins along the Z axis. The surface area becomes <math>1 cm \times 2 \pi 3.48/2 = 10.933 cm^2</math>. The beam pipe diameter assumed is 3.48 cm.
| |
| − | | |
| − | When filling the histogram binned 1 cm in Z, you should weight it by the amount of depositred energy divided by the circumference of the pipe and divided by the number of incident electrons on the target (5 million). The energy units are converted to keV by multiplying the numberator by 100 or in this case dividing by 5000 instead of 5 million.
| |
| − | | |
| − | | |
| − | TH1F *T00N=new TH1F("T00N","T00N",100,-1000.5,-0.5)
| |
| − | | |
| − | Electrons->Draw("evt.EoutPosZ>>T00N","evt.DepE/10.088/5000")
| |
| − | | |
| − | | |
| − | | |
| − | To convert From Mev/ e- to kW/cm^2 assuming a current of 1mA (10^-3 C/s) you
| |
| − | | |
| − | <math>\left( \frac{\mbox{MeV}}{\mbox{cm}^2 \mbox{e}^-}\right) \times \left( \frac{ \mbox{e}^-}{1.6 \times 10^{-19}\mbox{C}} \right ) \times \left( \frac{1 \times 10^{-3} \mbox{C}}{\mbox{s}} \right ) \times \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right )</math>
| |
| − | | |
| − | <math>\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )</math>
| |
| − | | |
| − | | |
| − | | |
| − |
| |
| − | {| border="1"
| |
| − | | [[File:BeamPipeDepEmev-vs-B.png |200px]] || [[File:BeamPipeDepPower-vs-B.png |200px]]|| [[File:BeamPipeDepPower-vs-lowB.png |200px]] | |
| − | |+ Energy deposited (MeV) along a 1 m long beam pipe of stainless steel 1.65 mm thick.
| |
| − | |}
| |
| − | | |
| − | With SS windows
| |
| − | Positrons->Draw("sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)","evt.BeamPosMomZ>0 && evt.BeamPosPosZ>-500 && sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)<97.4/2");
| |
| − | | |
| − | Positron Collection rates with '''60 cm''' long Solenoid
| |
| − |
| |
| − | {| border="1"
| |
| − | | [[File:PositronEventWithSolenoid_09-16-15A.png|200px]] ||[[File:PositronEventWith0.3Solenoid_09-16-15A.png|200px]]
| |
| − | |-
| |
| − | | When the solenoid is 1.5 Tesla, a 10 MeV electron produces a 6.5 MeV photon that pair produces a 4.4 MeV positron and a 1 MeV electron || Same Event but this time the solenoid is 0.3 Tesla and the positron hits the beam pipe, annihilates and makes two 511 keV photons
| |
| − | |+ Sample Positron Production Events
| |
| − | |}
| |
| − |
| |
| − | {| border="1"
| |
| − | | [[File:PositronEventWithSolenoid_09-16-15B.png|200px]] ||[[File:PositronEventWith0.3Solenoid_09-16-15B.png|200px]]
| |
| − | |-
| |
| − | | When the solenoid is set to 1.5 Tesla, a 10 MeV electron produces three photons less than 1 MeV in the target, two of them compton scatter in the beam pipe || The same event but this time the electron produces only 1 photon than ionizes in the target
| |
| − | |+ Sample Brem event producing no positrons
| |
| − | |}
| |
| − | | |
| − | | |
| − | With SS windows
| |
| − | Positrons->Draw("sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)","evt.BeamPosMomZ>0 && evt.BeamPosPosZ>-500 && sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)<97.4/2");
| |
| − | | |
| − | | |
| − | {| border="1"
| |
| − | {| border="1"
| |
| − | | B-field (Tesla) || || 34.8 mm diameter pipe || 47.5 || 60.2 || 72.9 || 97.4
| |
| | |- | | |- |
| − | | 0.0 || 0.35 || 1,2,4,4,5 || 2,3,4,4,6 || 4,4,6,7,9 || 6,8,9,10,11 || 16,14,15,16,17 | + | | outer beam pipe thickness || 0.165 cm |
| | |- | | |- |
| − | | 0.1 || ||225,236,250,246,249=241<math> \pm</math> 10 || 282,282,293,294,306=291<math> \pm</math> 10 || 373,366,370,364,373=369<math> \pm</math> 4 || 451,437,440,438,451=443<math> \pm</math> 7 || 602,584,563,558,570=575<math> \pm</math> 18 | + | | Solenoid inner radius || 2.527 cm |
| − | |-
| |
| − | | 0.3 || 0.35 || 626,619,596,619,611 =614<math> \pm</math> 11|| 720,726,706,730,717=720<math> \pm</math> 9|| 871,864,840,841,834 =850<math> \pm</math> 16|| 987,968,939,943,952 =958<math> \pm</math> 20|| 1118,1106,1069,1067,1080=1088<math> \pm</math> 23
| |
| | |- | | |- |
| − | | 0.6 || ||929,935,949,969,961=949<math> \pm</math> 17 ||1022,1031,1046,1059,1052 =1042<math> \pm</math> 15 || 1120,1130,1152,1154,1146 =1140<math> \pm</math> 15|| 1168,1184,1210,1221,1206 =1198<math> \pm</math> 21|| 1212, 1218,1240,1254,1242=1233<math> \pm</math> 18 | + | | Solenoid outer radius || 4.406 cm |
| − | |-
| |
| − | | 1.0 || 0.35 ||1117,1085,1083,1061,1085=1086<math> \pm</math> 20 || 1188,1154,1140,1111,1134=1145<math> \pm</math> 28||1225,1190,1178,1149,1172 =1183<math> \pm</math> 28||1243.1208,1195,1164,1184=1199<math> \pm</math> 30|| 1252,1219,1206,1178,1200=1211<math> \pm</math> 27
| |
| − | |-
| |
| − | | 1.5 || 0.22 ||
| |
| − | |-
| |
| − | | 2.0 || 0.10 ||1198,1210,1215,1223,1176=1204<math> \pm</math> 18 || 1216,1227,1235,1241,1196 =1223<math> \pm</math> 18|| 1237,1243,1252,1257,1214=1241<math> \pm</math> 17|| 1249,1252,1262,1266,1225 =1251<math> \pm</math> 16|| 1257,1262,1270,1276,1234=1260<math> \pm</math> 16
| |
| − | |-
| |
| − | | 4.0 || 0.002 ||
| |
| − | |+
| |
| | |} | | |} |
| | | | |
| − | | + | A comparison between the prediction from MCNPX and GEANT4 was once again performed. |
| | + | A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target. The target is positioned at Z = -902 mm. |
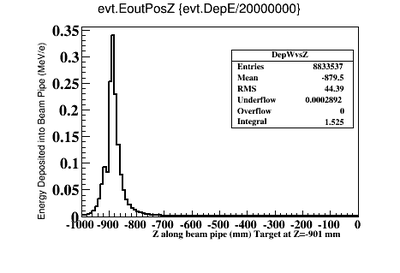
| | + | As shown in the figure below, GEANT4 predicts a peak energy deposition of 0.35 MeV/e while MCNPX predicts about 0.38 MeV/e. GEANT4 predicts a total of <math>3.08\times 10^7</math> MeV (the integral adds up the energy in each 1cm bin) of energy will be deposited in |
| | + | a 1m long beam pipe surrounding a 2 mm thick PbBi target located at Z=-902 mm when 20 million electrons impinge the target. The next step is to repeat his calculation in the presence of a solenoid surrounding the target. |
| | | | |
| | {| border="1" | | {| border="1" |
| − | | [[File:PositronRates-vs-SolenoidField_10-1-15.png |200px]] | + | | [[File:BeamPipeDepEmev_34.8_082915.png |400px]] || [[File:MCNPXBeamPipeDepEmev_34.8_090315.png |400px]] |
| − | |+ Positron Rates -vs- Solenoid Field for 2mm thick PbBi target and several Beam pipe diameters | + | |+ Energy deposited (MeV) in a 1 m long 3.48 cm diameter beam pipe surrounding a 2 mm target located at Z=-900 mm. |
| | |} | | |} |