Difference between revisions of "Niowave 12-2015"
(Created page with "The energy deposited by electrons scattered into a 3.48 diameter stainless steel beam pipe (1.65 mm thick) from a PbBi target as a function of a uniform Solenoidal magnetic fiel…") |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | + | Niowave Positron Project Progress for December 2015 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The energy deposited by electrons scattered into a 1.65 mm thick stainless steel beam pipe from the PbBi target as a function of a uniform solenoidal magnetic field was investigated for a 3.48 diameter stainless steel beam pipe. The simulation program GEANT4 was used to determine the amount of energy an electron lost in the stainless steel beam pipe. The beam pipe surface was divided into unit squares that were a centimeter in length and the energy deposited by a sample of 5 million electrons was summed for each unit square. The left side figure below shows a predicted peak energy deposition of 0.35 MeV/e^- in the 1.65 mm thick stainless steel beam pipe per 10 MeV electron impinging the 2 mm thick LBE target that has been sandwiched between two 0.25 mm thick stainless steel windows. | ||
| − | + | The energy deposited in the beam pipe can be converted to an average heat load if a average beam current is assumed. | |
| + | Under the assumption of a 1mA (10^-3 C/s) average beam current, the deposited energy (E_{dep}) per cm^2 per electron can be converted to the deposited power (P) per area using the equation | ||
| − | + | <math>P= E_{dep} \left( \frac{\mbox{MeV}}{\mbox{cm}^2 \mbox{e}^-}\right) \times \left( \frac{ \mbox{e}^-}{1.6 \times 10^{-19}\mbox{C}} \right ) \times \left( \frac{1 \times 10^{-3} \mbox{C}}{\mbox{s}} \right ) \times \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right ).</math> | |
| − | + | In other words, the energy deposited in units of keV/cm^2/e by a 1 mA electron beam is equivalent to a heat load in the units of Watts per cm^2. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<math>\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )</math> | <math>\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )</math> | ||
| − | + | Based on this observation the peak heat load, as shown in the figure below on the right, for a 1 mA electron beam is 35 W/cm^2. The electrons will begin to intersect a 3.48 diameter beam pipe less when the solenoidal magnetic field strength increases beyond one Tesla. A solenoidal field between two and four Tesla would substantially reduce the electron heat load on the beam pipe and place the positrons in a tight helical orbit for transportation. | |
{| border="1" | {| border="1" | ||
| − | | [[File:BeamPipeDepEmev-vs-B.png | | + | | [[File:BeamPipeDepEmev-vs-B.png |400px]] || [[File:BeamPipeDepPower-vs-B.png |400px]] |
|+ Energy deposited (MeV) along a 1 m long beam pipe of stainless steel 1.65 mm thick. | |+ Energy deposited (MeV) along a 1 m long beam pipe of stainless steel 1.65 mm thick. | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
Latest revision as of 15:19, 13 April 2016
Niowave Positron Project Progress for December 2015
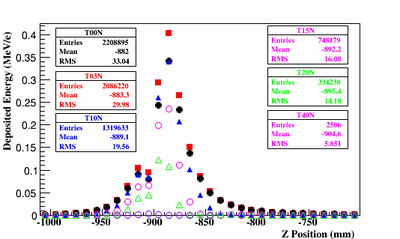
The energy deposited by electrons scattered into a 1.65 mm thick stainless steel beam pipe from the PbBi target as a function of a uniform solenoidal magnetic field was investigated for a 3.48 diameter stainless steel beam pipe. The simulation program GEANT4 was used to determine the amount of energy an electron lost in the stainless steel beam pipe. The beam pipe surface was divided into unit squares that were a centimeter in length and the energy deposited by a sample of 5 million electrons was summed for each unit square. The left side figure below shows a predicted peak energy deposition of 0.35 MeV/e^- in the 1.65 mm thick stainless steel beam pipe per 10 MeV electron impinging the 2 mm thick LBE target that has been sandwiched between two 0.25 mm thick stainless steel windows.
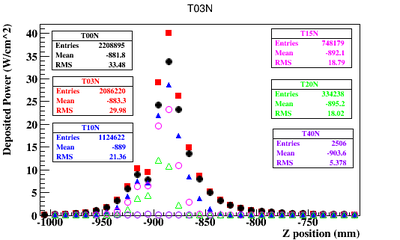
The energy deposited in the beam pipe can be converted to an average heat load if a average beam current is assumed. Under the assumption of a 1mA (10^-3 C/s) average beam current, the deposited energy (E_{dep}) per cm^2 per electron can be converted to the deposited power (P) per area using the equation
In other words, the energy deposited in units of keV/cm^2/e by a 1 mA electron beam is equivalent to a heat load in the units of Watts per cm^2.
Based on this observation the peak heat load, as shown in the figure below on the right, for a 1 mA electron beam is 35 W/cm^2. The electrons will begin to intersect a 3.48 diameter beam pipe less when the solenoidal magnetic field strength increases beyond one Tesla. A solenoidal field between two and four Tesla would substantially reduce the electron heat load on the beam pipe and place the positrons in a tight helical orbit for transportation.
 |
|