Difference between revisions of "Looking at effects of Solenoid on Phi Shifts"

From New IAC Wiki
Jump to navigation Jump to search
(Undo revision 105796 by Vanwdani (Talk))
 
(39 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
=[[Using Moller Data to alter energy range]]=
 
=[[Using Moller Data to alter energy range]]=
 +
 +
Using the Moller event file MollerScattering_NH3_4e8incident.dat, we can use the fact that GEMC will only recreate a particle based on the Moller electron.  While the data for the scattered electron is passed within a LUND file, kinematically this electron doesn't leave the beam line, and thus never enters the detectors to be recreated.  Since the solenoid's purpose is draw electrons trajectories closer the the beam line any electron close the the beam line will be drawn even closer, ensuring that it is never recreated in a GEMC simulation.
 +
 +
We can alter the energy conversion from MollerScattering_NH3_4e8incident.dat to investigate the energy-phi shift relationship
 +
 +
<center>[[File:FinalTheta.jpg]]</center>
 +
 +
 +
Plotting Scattering angle Theta vs. Total Energy for the Moller and scattered electron in the Lab frame.
 +
 +
<center>[[File:Theta_Energy_Lab.png]]</center>
 +
 +
 +
For the scattered electrons at theta of 90 degrees, these particles will not enter the detector and as a result are of no concern.  Zooming in on the Moller electron in the scattering angle theta vs. energy:
 +
 +
<center>[[File:Moller_Theta_E_lab.png]]</center>
 +
 +
 +
Using the fact that the minimum momentum of MollerScattering_NH3_4e8incident.dat is about 2 MeV,
 +
 +
<pre>
 +
awk 'NR == 1 {line = $0; min = $15} NR >1 && $15 < min {line =$0; min =$15} END{print line}' MollerScattering_NH3_4e8incident.dat
 +
 +
11000    0    0    11000.5    0    0    0    10997.9    1.42548    -0.177032    10998.4    0    0    0    2.01929    -1.42548    0.177032    2.01939    0    0    0 </pre>
 +
 +
and the maximum of about 5500 MeV,
 +
<pre>
 +
awk 'NR == 1 {line = $0; max = $15} NR >1 && $15 > max {line =$0; max =$15} END{print line}' MollerScattering_NH3_4e8incident.dat
 +
 +
11000    0    0    11000.5    0    0    0    5500.31    28.1338    -44.9298    5500.56    0    0    0    5498.52    -28.1338    44.9298    5498.78    0    0    0</pre>
 +
 +
At this energy for the scattered electron:
 +
 +
Relativistically, the x and y components remain the same in the conversion from the Lab frame to the Center of Mass frame, since the direction of motion is only in the z direction.
 +
 +
 +
 +
{| class="wikitable" align="center"
 +
| style="background: gray"      | <math>p^*_{2(x)}\Leftrightarrow p_{2(x)}'</math>
 +
|}
 +
 +
 +
{| class="wikitable" align="center"
 +
| style="background: gray"  | <math>p^*_{2(y)}\Leftrightarrow p_{2(y)}'</math>
 +
|}
 +
 +
 +
 +
{| class="wikitable" align="center"
 +
| style="background: gray"  | <math>p^*_{2(z)}=\sqrt {(p^*_2)^2-(p^*_{2(x)})^2-(p^*_{2(y)})^2}</math>
 +
|}
 +
 +
 +
 +
 +
<center>[[File:xz_lab.png | 400 px]]</center>
 +
<center>'''Figure 2: Definition of Moller electron variables in the Lab Frame in the x-z plane.'''</center>
 +
 +
 +
<center><math>\theta '_2\equiv \arccos \left(\frac{p^'_{2(z)}}{p^'_{2}}\right) = \arccos \left(\frac{28.1338}{5500.8154}\right) \approx 1.5</math> degrees</center>
 +
 +
This is still within the 7 degrees of the detector "cone" with respect to the beam line.
 +
 +
 +
We can alter the lines
 +
<pre>
 +
    Px=evt.FnlMom[0]/1000;
 +
                Py=evt.FnlMom[1]/1000;
 +
                Pz=evt.FnlMom[2]/1000;               
 +
                px=evt.MolMom[0]/1000;
 +
                py=evt.MolMom[1]/1000;
 +
                pz=evt.MolMom[2]/1000;
 +
               
 +
                KE=evt.FnlKE/1000;
 +
                ke=evt.MolKE/1000;
 +
</pre>
 +
 +
Dividing by 1 will give us a distribution of 2GeV-5500 GeV.
 +
 +
Divinding by 10 will give us a distribution of 0.2GeV-550 GeV
 +
 +
Dividing by 100 will give us a distribution of 0.02GeV-55 GeV
  
 
=[[Solenoid_effect_in_ 2_GeV_and_up_range|Solenoid effect > 2GeV]]=
 
=[[Solenoid_effect_in_ 2_GeV_and_up_range|Solenoid effect > 2GeV]]=
 +
 +
The number of of reconstructed GEMC events  registering a shift in their phi angle due to the magnetic field of the solenoid are recorded.  This is repeated for each of the five unique LUND files for each of the 7 magnetic fields being investigated.  A similar process of recording the number of phi shifts is repeated for each magnetic field.  Each quantity of phi shifts for non-zero magnetic fields  is normalized with respect to the number of phi shifts at with the corresponding LUND file for 0T (<math>x_i</math>).  This information is used to find the corrected sample standard deviation:
 +
 +
<center><math>\sigma \equiv \sqrt{\frac{1}{N-1} \sum_{k=1}^N (x_i+\bar{x})^2}</math></center>
 +
 +
 +
Creating a dat file with the magnetic field, phi shift, and the corrected sample standard deviation:
 +
 +
{| border=1 align=center
 +
  |+ Phi Change vs. Magnetic Field of Solenoid for 2-11GeV Moller Electrons
 +
|-
 +
  ! Magnetic Field (T)
 +
  ! <math>\Delta \ \phi </math>(degrees)
 +
  ! <math>\sigma</math>(degrees)
 +
|-
 +
  | -5
 +
  | 0.748315
 +
  | 0.0164881
 +
|-
 +
  | -2
 +
  | 0.899798
 +
  | 0.0147794
 +
|-
 +
  | 0
 +
  | 1
 +
  | 0
 +
|-
 +
  | 2
 +
  | 0.895382
 +
  | 0.0235786
 +
|-
 +
  | 4
 +
  | 0.809941
 +
  | 0.00795766
 +
|-
 +
  | 5
 +
  |  0.740047
 +
  | 0.0201546
 +
|-
 +
  | 6
 +
  | 0.708541
 +
  | 0.0172073
 +
|}
 +
 
 +
Xmgrace can be used to plot this:
 +
<center>[[File:GeV.png]]</center>
 +
 +
Investigating a plot of the distribution of the particles energy as a function of the change in the angle phi for the different magnetic fields.
 +
 +
<center>[[File:Composite_Fields.png]]</center>
  
 
=[[Solenoid effect in 200 MeV and up range|Solenoid effect > 200 MeV]]=
 
=[[Solenoid effect in 200 MeV and up range|Solenoid effect > 200 MeV]]=
 +
 +
Creating a dat file with the magnetic field, phi shift, and the corrected sample standard deviation:
 +
 +
{| border=1 align=center
 +
  |+ Phi Change vs. Magnetic Field of Solenoid for 2-11GeV Moller Electrons
 +
|-
 +
  ! Magnetic Field (T)
 +
  ! <math>\Delta \ \phi </math>(degrees)
 +
  ! <math>\sigma</math>(degrees)
 +
|-
 +
  | -5
 +
  | 0.0585341
 +
  | 0.00740803
 +
|-
 +
  | -2
 +
  | 0.138686
 +
  | 0.0308416
 +
|-
 +
  | 0
 +
  | 1
 +
  | 0
 +
|-
 +
  | 2
 +
  | 0.131325
 +
  | 0.0234678
 +
|-
 +
  | 4
 +
  | 0.0646613
 +
  | 0.0133132
 +
|-
 +
  | 5
 +
  |  0.059031
 +
  | 0.0122767
 +
|-
 +
  | 6
 +
  | 0.051293
 +
  | 0.00876825
 +
|}
 +
 
 +
Xmgrace can be used to plot this:
 +
<center>[[File:MeV.png]]</center>
  
 
=[[Solenoid effect  20 MeV and up|Solenoid effect > 20MeV]]=
 
=[[Solenoid effect  20 MeV and up|Solenoid effect > 20MeV]]=
  
−
 
+
No Phi shifts for Energies in this range where found in the simulation.
  
  

Latest revision as of 22:26, 14 April 2016

Using Moller Data to alter energy range

Using the Moller event file MollerScattering_NH3_4e8incident.dat, we can use the fact that GEMC will only recreate a particle based on the Moller electron. While the data for the scattered electron is passed within a LUND file, kinematically this electron doesn't leave the beam line, and thus never enters the detectors to be recreated. Since the solenoid's purpose is draw electrons trajectories closer the the beam line any electron close the the beam line will be drawn even closer, ensuring that it is never recreated in a GEMC simulation.

We can alter the energy conversion from MollerScattering_NH3_4e8incident.dat to investigate the energy-phi shift relationship

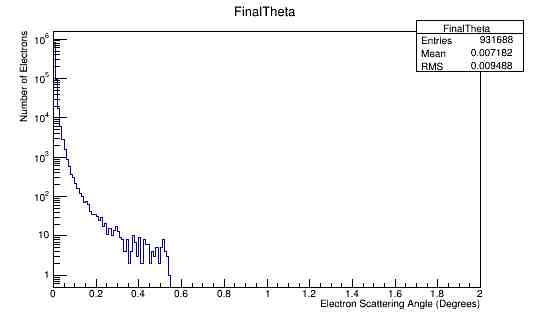
FinalTheta.jpg


Plotting Scattering angle Theta vs. Total Energy for the Moller and scattered electron in the Lab frame.

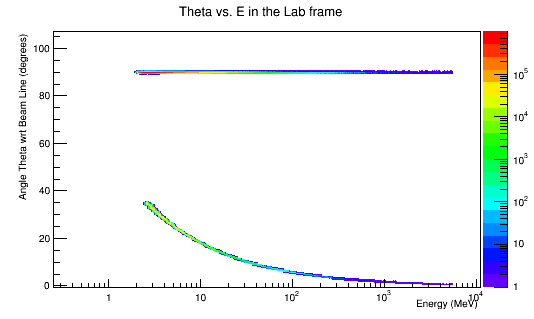
Theta Energy Lab.png


For the scattered electrons at theta of 90 degrees, these particles will not enter the detector and as a result are of no concern. Zooming in on the Moller electron in the scattering angle theta vs. energy:

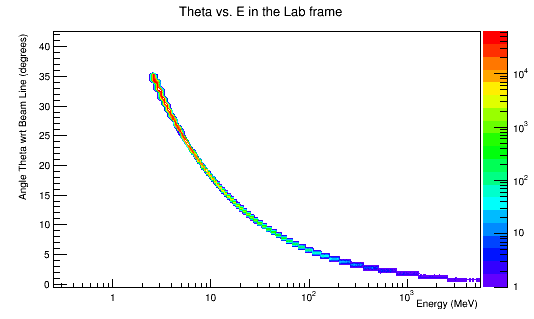
Moller Theta E lab.png


Using the fact that the minimum momentum of MollerScattering_NH3_4e8incident.dat is about 2 MeV, 

awk 'NR == 1 {line = $0; min = $15} NR >1 && $15 < min {line =$0; min =$15} END{print line}' MollerScattering_NH3_4e8incident.dat

11000    0     0     11000.5     0     0     0     10997.9     1.42548     -0.177032     10998.4     0     0     0     2.01929     -1.42548     0.177032     2.01939     0     0     0

and the maximum of about 5500 MeV, 

awk 'NR == 1 {line = $0; max = $15} NR >1 && $15 > max {line =$0; max =$15} END{print line}' MollerScattering_NH3_4e8incident.dat

11000    0     0     11000.5     0     0     0     5500.31     28.1338     -44.9298     5500.56     0     0     0     5498.52     -28.1338     44.9298     5498.78     0     0     0

At this energy for the scattered electron:

Relativistically, the x and y components remain the same in the conversion from the Lab frame to the Center of Mass frame, since the direction of motion is only in the z direction.


[math]p^*_{2(x)}\Leftrightarrow p_{2(x)}'[/math]


[math]p^*_{2(y)}\Leftrightarrow p_{2(y)}'[/math]


[math]p^*_{2(z)}=\sqrt {(p^*_2)^2-(p^*_{2(x)})^2-(p^*_{2(y)})^2}[/math]



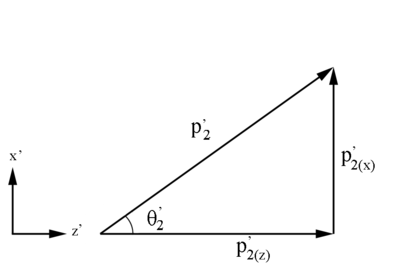
Xz lab.png
Figure 2: Definition of Moller electron variables in the Lab Frame in the x-z plane.


[math]\theta '_2\equiv \arccos \left(\frac{p^'_{2(z)}}{p^'_{2}}\right) = \arccos \left(\frac{28.1338}{5500.8154}\right) \approx 1.5[/math] degrees

This is still within the 7 degrees of the detector "cone" with respect to the beam line.


We can alter the lines 

    Px=evt.FnlMom[0]/1000;
                Py=evt.FnlMom[1]/1000;
                Pz=evt.FnlMom[2]/1000;                
                px=evt.MolMom[0]/1000;
                py=evt.MolMom[1]/1000;
                pz=evt.MolMom[2]/1000;
                
                KE=evt.FnlKE/1000;
                ke=evt.MolKE/1000;

Dividing by 1 will give us a distribution of 2GeV-5500 GeV.

Divinding by 10 will give us a distribution of 0.2GeV-550 GeV

Dividing by 100 will give us a distribution of 0.02GeV-55 GeV

Solenoid effect > 2GeV

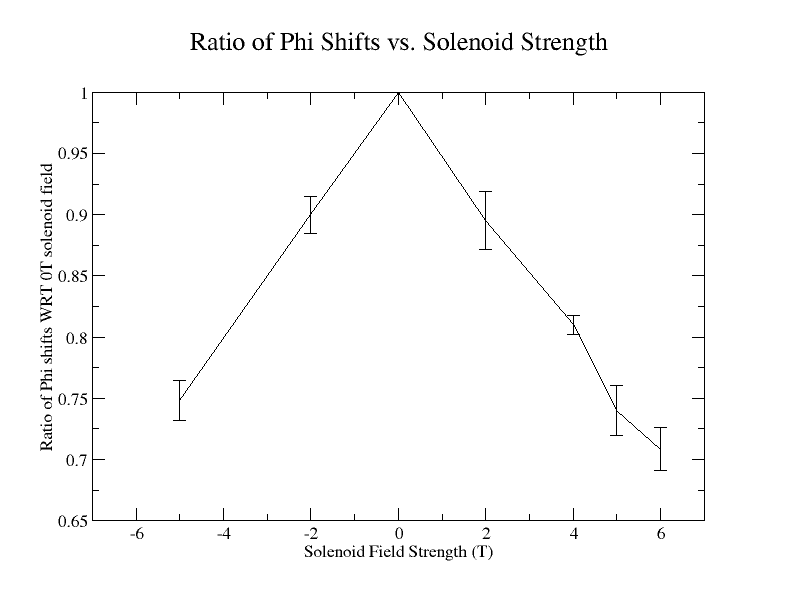
The number of of reconstructed GEMC events registering a shift in their phi angle due to the magnetic field of the solenoid are recorded. This is repeated for each of the five unique LUND files for each of the 7 magnetic fields being investigated. A similar process of recording the number of phi shifts is repeated for each magnetic field. Each quantity of phi shifts for non-zero magnetic fields is normalized with respect to the number of phi shifts at with the corresponding LUND file for 0T ([math]x_i[/math]). This information is used to find the corrected sample standard deviation:

[math]\sigma \equiv \sqrt{\frac{1}{N-1} \sum_{k=1}^N (x_i+\bar{x})^2}[/math]


Creating a dat file with the magnetic field, phi shift, and the corrected sample standard deviation:

Phi Change vs. Magnetic Field of Solenoid for 2-11GeV Moller Electrons
Magnetic Field (T) [math]\Delta \ \phi [/math](degrees) [math]\sigma[/math](degrees)
-5 0.748315 0.0164881
-2 0.899798 0.0147794
0 1 0
2 0.895382 0.0235786
4 0.809941 0.00795766
5 0.740047 0.0201546
6 0.708541 0.0172073

Xmgrace can be used to plot this:

GeV.png

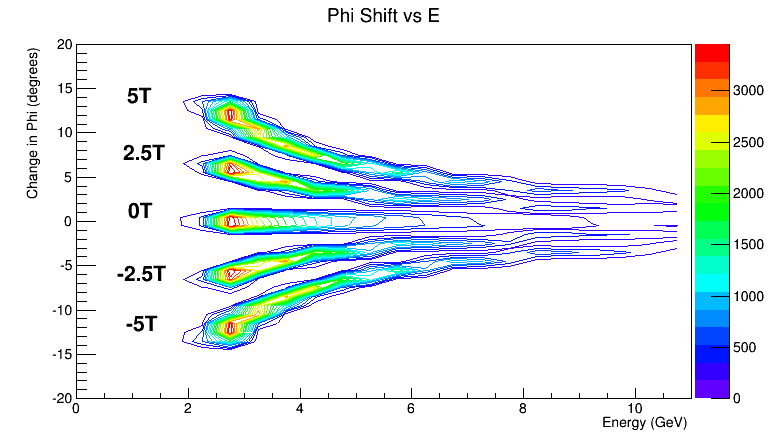
Investigating a plot of the distribution of the particles energy as a function of the change in the angle phi for the different magnetic fields.

Composite Fields.png

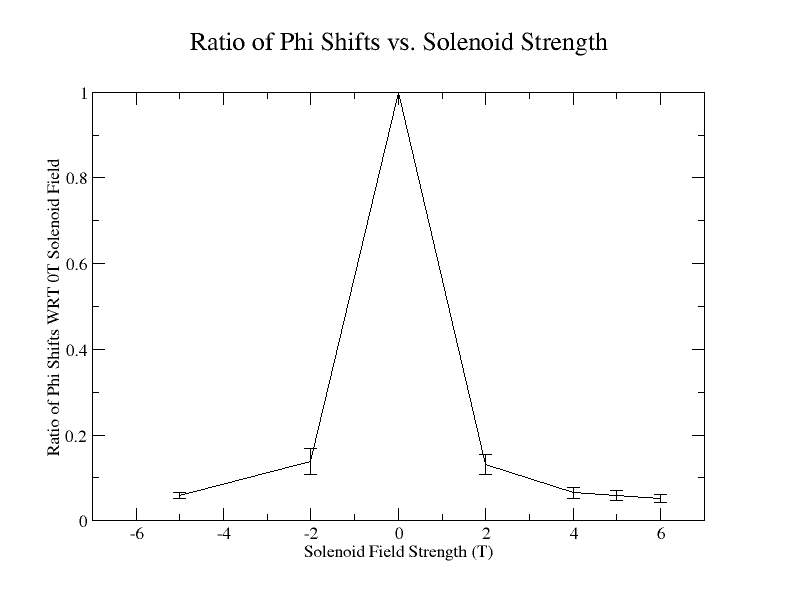
Solenoid effect > 200 MeV

Creating a dat file with the magnetic field, phi shift, and the corrected sample standard deviation:

Phi Change vs. Magnetic Field of Solenoid for 2-11GeV Moller Electrons
Magnetic Field (T) [math]\Delta \ \phi [/math](degrees) [math]\sigma[/math](degrees)
-5 0.0585341 0.00740803
-2 0.138686 0.0308416
0 1 0
2 0.131325 0.0234678
4 0.0646613 0.0133132
5 0.059031 0.0122767
6 0.051293 0.00876825

Xmgrace can be used to plot this:

MeV.png

Solenoid effect > 20MeV

No Phi shifts for Energies in this range where found in the simulation.


Links

Back

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Looking_at_effects_of_Solenoid_on_Phi_Shifts&oldid=105797"