Difference between revisions of "DV Creating LUND Files"

From New IAC Wiki
Jump to navigation Jump to search
 
(55 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
=The LUND format=
 
=The LUND format=
 +
The LUND file format is broken into two parts. The first part of the format is the header, which basically tells how many particles follow this line.  For Moller scattering, this number should always be two electrons.  The second component of the LUND format contains the kinematic variable for the scattered electron and the Moller electron.
  
 +
The LUND format has extra variables that are not utilized within GEMC.  Only the '''BOLD''' variables are necessary within GEMC simulations.[1]
 +
 +
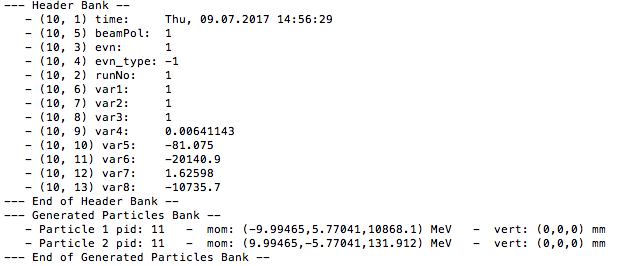
NOTE: Newer versions of GEMC use different format header.  GEMC 2.4 and 2.6 are run for the same 10 events under the same circumstances with identical gcard files.  The ouput is displayed in text format instead of evio.
 +
 +
 +
GEMC 2.4
 +
[[File:HeaderGEMC2_4.png]]
 +
 +
 +
 +
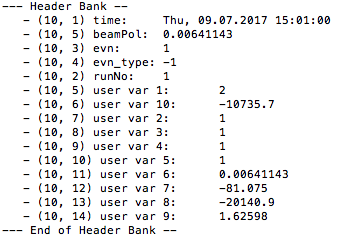
LUND File info for header
 +
[[File:HeaderLUND.png]]
 +
 +
 +
 +
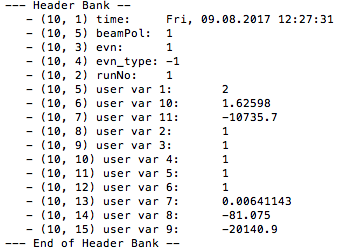
GEMC 2.6
 +
[[File:HeaderGEMC2_6.png]]
 +
 +
 +
GEMC 2.4 had been taking the 5th element on the first line of each LUND event, the beam polization for the 5th entry in the header array (10,5).  Newer GEMC is grabbing the 6th element of the first line of each LUND event.
 +
 +
This can be fixed by adding an additional column with value 1 every 3rd row to the LUND file.
 +
 +
<pre>
 +
sed -i -e '1i\ \' LH2_0Sol_0Tor_11GeV_IsotropicPhi_ShieldOut*/LH2_0Sol_0Tor_11GeV_IsotropicPhi_ShieldOut_*.LUND
 +
</pre>
 +
 +
[[File:HeaderGEMC2_6fix.png]]
 
==The Header==
 
==The Header==
 
{| border=1 align=center
 
{| border=1 align=center
Line 55: Line 84:
 
This represents the polarization of the electron beam, either negative or positive 1.  This value is always set to positive 1.
 
This represents the polarization of the electron beam, either negative or positive 1.  This value is always set to positive 1.
  
−
==6:x==
+
===6:x===
−
This represents the Bjorken x scaling variable.   
+
This represents the Bjorken x scaling variable.  [2]
  
 
<math>x=\frac{-q^2}{2p\cdot q}=\frac{-q^2}{2M\nu}=\frac{Q^2}{2M\nu}</math>
 
<math>x=\frac{-q^2}{2p\cdot q}=\frac{-q^2}{2M\nu}=\frac{Q^2}{2M\nu}</math>
Line 63: Line 92:
 
Where M is the rest mass-energy of the proton<math> M\approx 938MeV</math>
 
Where M is the rest mass-energy of the proton<math> M\approx 938MeV</math>
  
−
==7:y==
+
===7:y===
−
<math>y=\frac{p\cdot q}{p\cdot k}=\frac{\nu}{E_i}=\frac{E_i-E_f}{E_i}</math>
+
<math>y=\frac{p\cdot q}{p\cdot k}=\frac{\nu}{E_i}=\frac{E_i-E_f}{E_i}</math>[2]
  
−
==8:W==
+
===8:W===
  
 
The invariant mass of the final hadronic system
 
The invariant mass of the final hadronic system
Line 73: Line 102:
 
<math>W^2\equiv (p+q)^2=M^2+2M\nu+q^2=M^2+2M\nu-Q^2</math>
 
<math>W^2\equiv (p+q)^2=M^2+2M\nu+q^2=M^2+2M\nu-Q^2</math>
  
−
==9:<math>Q^2</math>==
+
===9:<math>Q^2</math>===
−
This represents the squared 4-momentum-transfer vector q of the exchanged virtual photon.
+
This represents the squared 4-momentum-transfer vector q of the exchanged virtual photon.[3]
  
  
Line 85: Line 114:
 
<math>q\equiv k_i-k_f</math>
 
<math>q\equiv k_i-k_f</math>
  
−
==10:<math>\nu</math>==
+
===10:<math>\nu</math>===
 
This represents the energy loss between scattering electrons.   
 
This represents the energy loss between scattering electrons.   
  
Line 96: Line 125:
  
  
−
where E<sub>i</sub> and E<sub>f</sup> are the initial and final electron energies.
+
where E<sub>i</sub> and E<sub>f</sub> are the initial and final electron energies.
 +
 
 +
==Particles==
  
 
{| border=1 align=center
 
{| border=1 align=center
−
   |+ LUND Header
+
   |+ Particle Data
 
|-
 
|-
 
   ! Column
 
   ! Column
Line 147: Line 178:
 
|}
 
|}
  
−
=Writing LUND files=
 
  
−
=Correct for vertex location=
+
Where
 +
===1:Index===
 +
From the header line 1, which states how many particles follow, this counts in increments of one up to the required number.
 +
 
 +
===2:Charge===
 +
-1, 0, 1
 +
 
 +
===3:Type===
 +
1 denotes that this is an active particle that can interact within the simulation.
 +
 
 +
===4:Particle ID===
 +
This quantity follows the Particle Data Group Monte Carlo numbering scheme for representing what type of particle is simulated.[4]
 +
 
 +
[[File:MontecarlorPDGparticleID.pdf]]
 +
 
 +
===5:Parent Index===
 +
This signifies if the particle can be considered a primary (=0) or secondary particle.  For this simulation, GEMC does not utilize this variable and all values have been set to 0
 +
 
 +
===6:Daughter Index===
 +
This signifies if the particle has created secondary particles.  For this simulation, GEMC does not utilize this variable and all values have been set to 0.
 +
 
 +
===7:Momentum x===
 +
This is the value of the momentum vector in the x direction.  Values must be given in GeV.
 +
 
 +
===8:Momentum y===
 +
This is the value of the momentum vector in the y direction.  Values must be given in GeV.
 +
 
 +
===9:Momentum z===
 +
This is the value of the momentum vector in the z direction.  Values must be given in GeV.
 +
 
 +
===10:E===
 +
E is the total relativistic energy,
 +
 
 +
<math>E\equiv \sqrt{p^2+m^2}</math>
 +
 
 +
For the Ultrarelativistic limit,
 +
 
 +
<math>E\approx p\ \ \ </math>Since <math>p\ggg m</math>
 +
 
 +
===11:Mass===
 +
This represents the rest mass-energy of the particle being simulated.  For Moller scattering this value has been set to .000511 GeV.
 +
 
 +
===12:Vertex x===
 +
This represents the x position within the eg12 detector at time t=0.
 +
 
 +
===13:Vertex y===
 +
This represents the y position within the eg12 detector at time t=0.
 +
 
 +
===14:Vertex z===
 +
This represents the z position within the eg12 detector at time t=0.
 +
 
 +
 
 +
----
 +
 
 +
=Links=
 +
 
 +
[[DV_RunGroupC_Moller#Creating_LUND_Files|Back]]

Latest revision as of 18:47, 8 September 2017

The LUND format

The LUND file format is broken into two parts. The first part of the format is the header, which basically tells how many particles follow this line. For Moller scattering, this number should always be two electrons. The second component of the LUND format contains the kinematic variable for the scattered electron and the Moller electron.

The LUND format has extra variables that are not utilized within GEMC. Only the BOLD variables are necessary within GEMC simulations.[1]

NOTE: Newer versions of GEMC use different format header. GEMC 2.4 and 2.6 are run for the same 10 events under the same circumstances with identical gcard files. The ouput is displayed in text format instead of evio.


GEMC 2.4 HeaderGEMC2 4.png


LUND File info for header HeaderLUND.png


GEMC 2.6 HeaderGEMC2 6.png


GEMC 2.4 had been taking the 5th element on the first line of each LUND event, the beam polization for the 5th entry in the header array (10,5). Newer GEMC is grabbing the 6th element of the first line of each LUND event.

This can be fixed by adding an additional column with value 1 every 3rd row to the LUND file. 

sed -i -e '1i\ \' LH2_0Sol_0Tor_11GeV_IsotropicPhi_ShieldOut*/LH2_0Sol_0Tor_11GeV_IsotropicPhi_ShieldOut_*.LUND

HeaderGEMC2 6fix.png

The Header

LUND Header
Column Quantity
1
Number of Particles
2
Number of Target Nucleons
3
Number of Target Protons
4
Target Polarization
5
Beam Polarization
6
x
7
y
8
W
9
[math]Q^2[/math]
10
[math]\nu[/math]

Where

1:Number of Particles

This line tells how many particles follow the header line. For Moller Scattering, this number should always be 2.

2:Number of Target Nucleons

For this simulation, only an electron-electron collision is considered. This quantity is always set to 1 for the one stationary electron we consider the incident electron scattering from.

3:Number of Target Protons

For Moller Scattering, there are no target protons. This number is set to 1, but does not have any effect within the GEMC simulations.

4:Target Polarization

This represents the polarization of the target material, either positive or negative 1. This value is always set to 1 and has no effect within the GEMC simulations.

5:Beam Polarization

This represents the polarization of the electron beam, either negative or positive 1. This value is always set to positive 1.

6:x

This represents the Bjorken x scaling variable. [2]

[math]x=\frac{-q^2}{2p\cdot q}=\frac{-q^2}{2M\nu}=\frac{Q^2}{2M\nu}[/math]


Where M is the rest mass-energy of the proton[math] M\approx 938MeV[/math]

7:y

[math]y=\frac{p\cdot q}{p\cdot k}=\frac{\nu}{E_i}=\frac{E_i-E_f}{E_i}[/math][2]

8:W

The invariant mass of the final hadronic system


[math]W^2\equiv (p+q)^2=M^2+2M\nu+q^2=M^2+2M\nu-Q^2[/math]

9:[math]Q^2[/math]

This represents the squared 4-momentum-transfer vector q of the exchanged virtual photon.[3]


[math]Q^2\equiv -q^2[/math]


Where q is the momentum transfer betwwn the incident electron and target via the virtual photon.


[math]q\equiv k_i-k_f[/math]

10:[math]\nu[/math]

This represents the energy loss between scattering electrons.

[math]\nu = \frac{p\cdot q}{M}[/math]

This can be written in the Lab frame as:


[math]\nu\equiv E_i-E_f[/math]


where Ei and Ef are the initial and final electron energies.

Particles

Particle Data
Column Quantity
1
Index
2
Charge
3
Type (1 is active)
4
Particle ID
5
Parent Index
6
Daughter Index
7
Momentum x (GeV)
8
Momentum y (GeV)
9
Momentum z (GeV)
10
[math]E[/math]
11
Mass
12
Vertex x (cm)
13
Vertex y (cm)
14
Vertex z (cm)


Where

1:Index

From the header line 1, which states how many particles follow, this counts in increments of one up to the required number.

2:Charge

-1, 0, 1

3:Type

1 denotes that this is an active particle that can interact within the simulation.

4:Particle ID

This quantity follows the Particle Data Group Monte Carlo numbering scheme for representing what type of particle is simulated.[4]

File:MontecarlorPDGparticleID.pdf

5:Parent Index

This signifies if the particle can be considered a primary (=0) or secondary particle. For this simulation, GEMC does not utilize this variable and all values have been set to 0

6:Daughter Index

This signifies if the particle has created secondary particles. For this simulation, GEMC does not utilize this variable and all values have been set to 0.

7:Momentum x

This is the value of the momentum vector in the x direction. Values must be given in GeV.

8:Momentum y

This is the value of the momentum vector in the y direction. Values must be given in GeV.

9:Momentum z

This is the value of the momentum vector in the z direction. Values must be given in GeV.

10:E

E is the total relativistic energy,

[math]E\equiv \sqrt{p^2+m^2}[/math]

For the Ultrarelativistic limit,

[math]E\approx p\ \ \ [/math]Since [math]p\ggg m[/math]

11:Mass

This represents the rest mass-energy of the particle being simulated. For Moller scattering this value has been set to .000511 GeV.

12:Vertex x

This represents the x position within the eg12 detector at time t=0.

13:Vertex y

This represents the y position within the eg12 detector at time t=0.

14:Vertex z

This represents the z position within the eg12 detector at time t=0.


Links

Back

Retrieved from "https://wiki.iac.isu.edu/index.php?title=DV_Creating_LUND_Files&oldid=118103"