Difference between revisions of "Old work"
(Created page with "===Moller Differential Cross Section=== Using the equation from [1] <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ e^4 }{8E^{*2}}\left \{\frac{1+cos^4(\frac{\theta^*}{2})}{sin…") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 42: | Line 42: | ||
We find that the differential cross section scale is <math>\frac{d\sigma}{d\Omega}\approx .5\times 10^{-3}mb=.5\mu b</math> | We find that the differential cross section scale is <math>\frac{d\sigma}{d\Omega}\approx .5\times 10^{-3}mb=.5\mu b</math> | ||
| + | |||
| + | ===Different p<sub>2</sub><sup>1</sup> Values=== | ||
| + | |||
| + | Using the conversion of | ||
| + | |||
| + | |||
| + | <center><math>\frac{1}{1GeV^2}=.3894 mb</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\sigma=\int d\sigma=\int \frac{d\sigma}{d\Omega_2'}d\Omega</math></center> | ||
| + | |||
| + | |||
| + | The range of the detector is considered to be <math> .10 \le \theta \le .87</math>,<math>-\pi \le \phi \le \pi</math> | ||
| + | |||
| + | |||
| + | <center><math>\sigma=\int_{ .611}^{2.531} \int_{-\pi}^{\pi} \frac{d\sigma}{d\Omega_2'}sin\theta \,d\theta \, d\phi </math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\sigma=2\pi \int_{.611}^{2.531} \frac{d\sigma}{d\Omega_2'} sin\theta \,d\theta </math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\sigma=2\pi (1.638)\frac{d\sigma}{d\Omega_2'} </math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\sigma=(10.294) \frac{d\sigma}{d\Omega_2'} </math></center> | ||
| + | |||
| + | |||
| + | {| class="wikitable" align="center" border=1 | ||
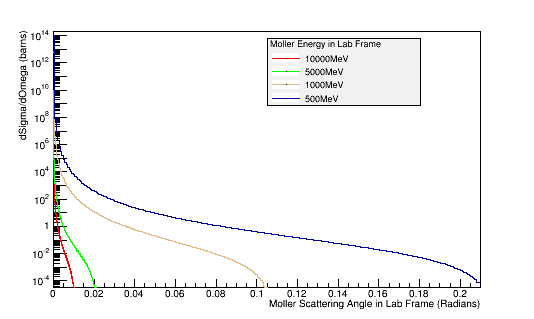
| + | |+ '''Differential Cross Section Scale for Different p<sub>2</sub><sup>1</sup> Values''' | ||
| + | |- | ||
| + | ! <math>p_{2}'(MeV)</math> | ||
| + | ! <math>\frac{d\sigma}{d\Omega_{2}^'}(eV^{-2})</math> | ||
| + | ! <math>\frac{d\sigma}{d\Omega_{2}^'}(GeV^{-2})</math> | ||
| + | ! <math>\frac{d\sigma}{d\Omega_{2}^'}(mb)</math> | ||
| + | ! <math>\frac{d\sigma}{d\Omega_{2}^'}(b)</math> | ||
| + | ! <math>\sigma(b)</math> | ||
| + | |- | ||
| + | | <math>10000</math> | ||
| + | | <math>9.357\times 10^{-11}</math> | ||
| + | | <math>9.357\times 10^{7}</math> | ||
| + | | <math>3.644\times 10^{7}</math> | ||
| + | | <math>3.644\times 10^{4}</math> | ||
| + | | <math>3.751\times 10^{5}</math> | ||
| + | |- | ||
| + | | <math>5000 </math> | ||
| + | | <math>3.743\times 10^{-10}</math> | ||
| + | | <math>3.743\times 10^{8}</math> | ||
| + | | <math>1.458\times 10^{8}</math> | ||
| + | | <math>1.458\times 10^{5}</math> | ||
| + | | <math>1.501\times 10^{6}</math> | ||
| + | |- | ||
| + | | <math>1000 </math> | ||
| + | | <math>9.357\times 10^{-9}</math> | ||
| + | | <math>9.357\times 10^{9}</math> | ||
| + | | <math>3.644\times 10^{9}</math> | ||
| + | | <math>3.644\times 10^{6}</math> | ||
| + | |<math>3.751\times 10^{7}</math> | ||
| + | |- | ||
| + | | <math>500</math> | ||
| + | | <math>3.743\times 10^{-8}</math> | ||
| + | | <math>3.743\times 10^{10}</math> | ||
| + | | <math>1.458\times 10^{10}</math> | ||
| + | | <math>1.458\times 10^{7}</math> | ||
| + | | <math>1.501\times 10^{8}</math> | ||
| + | |} | ||
| + | |||
| + | ===CM to Lab Frame=== | ||
| + | We can substitute in for <math>\theta</math> | ||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 }{4E^{*2}}\frac{ (3+cos^2\theta^*)^2}{sin^4\theta^*}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 }{4E^{*2}}\frac{ (3+cos^2\theta^*)^2}{sin(\theta^*)sin(\theta^*)sin(\theta^*)sin(\theta^*)}</math></center> | ||
| + | |||
| + | |||
| + | Using, | ||
| + | <center><math>sin(\theta^*)=sin(\theta_{2}^*)=\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)</math></center> | ||
| + | |||
| + | |||
| + | {| class="wikitable" align="center" | ||
| + | | style="background: gray" | <math>\frac{\partial ^2\sigma(E,\, \theta ,\, \phi)}{\partial E\, \partial \Omega} = \frac{\partial ^2\sigma^*(E^*,\, \theta^* ,\, \phi^*)}{\partial E^*\,\partial \Omega^*}\frac{p}{p^{*}}</math> | ||
| + | |} | ||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 }{4E^{*2}}\frac{ (3+cos^2\theta^*)^2}{\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (3+cos^2\theta^*)^2}{sin^4 \left( \theta_{2}'\right)}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | Now, using the trigometric identity, | ||
| + | <center><math>sin^2 t+cos^2 t=1\Longrightarrow cos^2(\theta^*)=1-sin^2(\theta^*)</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (3+1-sin^2(\theta^*))^2}{sin^4 \left( \theta_{2}'\right)}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (4-sin(\theta^*)sin(\theta^*))^2}{sin^4 \left( \theta_{2}'\right)}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (4-\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right))^2}{sin^4 \left( \theta_{2}'\right)}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (4-\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right))^2}{sin^4 \left( \theta_{2}'\right)}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (16-8\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right)+\frac{p_{2}^{'4}}{p_{2}^{*4}}\ sin^4 \left( \theta_{2}'\right))}{sin^4 \left( \theta_{2}'\right)}</math></center> | ||
| + | |||
| + | |||
| + | Substituting, | ||
| + | <center><math>p_{2}^*=\sqrt{E_{2}^{*2}-m^2}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 (\sqrt{E_{2}^{*2}-m^2})^4}{4E^{*2}p_{2}'^4}\frac{ (16-8\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right)+\frac{p_{2}^{'4}}{p_{2}^{*4}}\ sin^4 \left( \theta_{2}'\right))}{sin^4 \left( \theta_{2}'\right)}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 (E_{2}^{*2}-m^2)^2}{4E^{*2}p_{2}'^4}\frac{ (16-8\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right)+\frac{p_{2}^{'4}}{p_{2}^{*4}}\ sin^4 \left( \theta_{2}'\right))}{sin^4 \left( \theta_{2}'\right)}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | Substituting in for m, E<sub>2</sub><sup>*,</sup>and E<sup>*</sup> | ||
| + | <math>\alpha^2=5.3279\times 10^{-5}</math> | ||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=(\frac{ 5.3279\times 10^{-5}( ((53.015MeV)^{2}-(.511MeV)^2)^2}{4\times (106.031MeV)^{2}p_{2}'^4}\frac{ (16-8\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right)+\frac{p_{2}^{'4}}{p_{2}^{*4}}\ sin^4 \left( \theta_{2}'\right))}{sin^4 \left( \theta_{2}'\right)}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega '_1}=\frac{9.357\times 10^9eV^2}{p_{2}^{'4}}\frac{ (16-8\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right)+\frac{p_{2}^{'4}}{p_{2}^{*4}}\ sin^4 \left( \theta_{2}'\right))}{sin^4 \left( \theta_{2}'\right)}</math></center> | ||
| + | ===Substituting for Moller range and energies=== | ||
| + | Converting the number of electrons to barns, | ||
| + | |||
| + | |||
| + | <center><math>\frac{d\sigma}{d\Omega_{2}'}=\frac{dN}{\mathcal L d\Omega}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <center><math>\Longrightarrow dN=\frac{d \sigma}{d \Omega} \mathcal L</math></center> | ||
| + | |||
| + | |||
| + | <center><math>where \mathcal L=i\, \rho I</math></center> | ||
| + | |||
| + | |||
| + | where ρ<sub>target</sub> is the density of the target material, l<sub>target</sub> is the length of the target, and N is the number of incident particles scattered. | ||
| + | |||
| + | |||
| + | <center><math>\mathcal L=\frac{.86g}{1 cm^3}\times \frac{(100cm)^3}{1m^3} \times \frac{1 kg}{1000 g}\times \left[ \left(.75 \frac{1 mole}{1.01 g} \times \frac{1000g}{1 kg} \right)+\left(.25 \frac{1 mole}{14.01 g} \times \frac{1000g}{1 kg} \right)\right] \times \frac{6.022\times10^{23}particles}{1 mole} \times \frac{1cm}{100 cm} \times \frac{1 m}{ } \times \frac{10^{-28} m^2}{barn} </math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\mathcal L=\frac{860kg}{1 m^3}\times \left[ \left(\frac{742.574 mole}{kg} \right)+\left(\frac{17.844 mole}{1 kg} \right)\right] \times \frac{6.022\times 10^{-7}\ particles\cdot m^3}{1 mole\cdot barn} </math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <center><math>\mathcal L=\frac{5.170\times 10^{-4}kg\cdot particles}{1 mole\cdot barn} \left(\frac{760.418 mole}{kg} \right)</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\mathcal L=\frac{.394\ particles}{1 barn} </math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\Longrightarrow N=\sigma \frac{.394\ particles}{1 barn}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | {| class="wikitable" align="center" border=1 | ||
| + | |+ '''Number of electrons from Moller electron Momentum''' | ||
| + | |- | ||
| + | ! <math>p_2^{'}(MeV/c)</math> | ||
| + | ! <math>\sigma(b)</math> | ||
| + | ! <math>Number of electrons</math> | ||
| + | |- | ||
| + | | <math>\equiv 10000</math> | ||
| + | | <math>3.751\times 10^{5}</math> | ||
| + | |<math>\approx 1.478\times 10^5</math> | ||
| + | |- | ||
| + | | <math>\equiv 5000 </math> | ||
| + | | <math>1.501\times 10^{6}</math> | ||
| + | |<math>\approx5.914\times 10^5</math> | ||
| + | |- | ||
| + | | <math>\equiv 1000 </math> | ||
| + | |<math>3.751\times 10^{7}</math> | ||
| + | |<math>\approx 1.478\times 10^7</math> | ||
| + | |- | ||
| + | | <math>\equiv 500</math> | ||
| + | | <math>1.501\times 10^{8}</math> | ||
| + | |<math>\approx 5.914\times 10^7</math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | <center>[[File:Lab_Frame_Moller_DiffX.png]]</center> | ||
Latest revision as of 19:29, 9 March 2016
Moller Differential Cross Section
Using the equation from [1]
This can be simplified to the form
Plugging in the values expected for 2 scattering electrons:
Using unit analysis on the term outside the parantheses, we find that the differential cross section for an electron at this momentum should be around
Using the conversion of
We find that the differential cross section scale is
Different p21 Values
Using the conversion of
The range of the detector is considered to be ,
CM to Lab Frame
We can substitute in for
Using,
Now, using the trigometric identity,
Substituting,
Substituting in for m, E2*,and E*
Substituting for Moller range and energies
Converting the number of electrons to barns,
where ρtarget is the density of the target material, ltarget is the length of the target, and N is the number of incident particles scattered.