Difference between revisions of "Known Moller differential cross section"
| (30 intermediate revisions by the same user not shown) | |||
| Line 29: | Line 29: | ||
<center><math>\frac{5.3279\times 10^{-5}}{4\times 2.81\times 10^{15}eV^2}=4.74\times 10^{-21} eV^{-2}=\frac{4.74\times 10^{-21}}{1eV^2}\times \frac{1\times 10^{18}eV^2 }{1\ GeV^2}=\frac{.0047}{GeV^2}</math></center> | <center><math>\frac{5.3279\times 10^{-5}}{4\times 2.81\times 10^{15}eV^2}=4.74\times 10^{-21} eV^{-2}=\frac{4.74\times 10^{-21}}{1eV^2}\times \frac{1\times 10^{18}eV^2 }{1\ GeV^2}=\frac{.0047}{GeV^2}</math></center> | ||
| + | |||
| + | |||
| + | The trigonometric function part of the equation comes out to it's minimum of 9 at 90 degrees. | ||
| + | |||
| + | |||
| + | <center><math>\frac{(3+Cos^2(90))^2}{Sin^4(90)}=9</math></center> | ||
| + | |||
| + | |||
Using the conversion of | Using the conversion of | ||
| Line 38: | Line 46: | ||
<center><math>\frac{1\ GeV^{-2}}{.3894\ mb}=\frac{.0047\ GeV^{-2}}{x\ mb}</math></center> | <center><math>\frac{1\ GeV^{-2}}{.3894\ mb}=\frac{.0047\ GeV^{-2}}{x\ mb}</math></center> | ||
| − | We find that the differential cross section scale is <math>\frac{d\sigma}{d\Omega}\approx 1.8\times 10^{-3}mb=1.8\mu b</math> | + | We find that the differential cross section scale is <math>\frac{d\sigma}{d\Omega}\approx 1.8\times 10^{-3}mb=1.8\mu b\times 9=17\mu b</math> |
| Line 44: | Line 52: | ||
Converting the number of electrons to barns, | Converting the number of electrons to barns, | ||
| − | + | <center><math>L=\frac{i_{scattered}}{\sigma} \approx i_{scattered}\times \rho_{target}\times l_{target}</math></center> | |
| + | |||
| + | |||
| + | where ρ<sub>target</sub> is the density of the target material, l<sub>target</sub> is the length of the target, and i<sub>scattered</sub> is the number of incident particles scattered. | ||
| + | |||
| + | |||
| + | For a ammonia target, | ||
| + | |||
| + | Ammonia density: | ||
| + | |||
| + | <math>\rho = \frac{.8 g}{cm^3}</math> | ||
| + | |||
| + | |||
| + | Molecular weight calculation: | ||
| + | |||
| + | <math>\frac{14.0067 g}{1 mole} + \frac{1.00794 g}{1 mole}\times 3=\frac{17 g}{1 mole}</math> | ||
| + | |||
| + | |||
| + | :::::<math>\rho_{target}\times l_{target}=\frac{.8 g}{1 cm^3}\times \frac{1 mole}{17 g} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1 cm}{ } \times \frac{10^{-24} cm^2}{barn} =2.82\times 10^{-2} barns</math> | ||
| + | |||
| + | |||
| + | |||
| + | For 400 million incoming electrons | ||
| + | |||
| + | |||
| + | :::::<math>\frac{1}{\rho_{target}\times l_{target} \times 4 \times 10^8}=8.87\times 10^{-8} barns</math> | ||
| + | |||
| − | |||
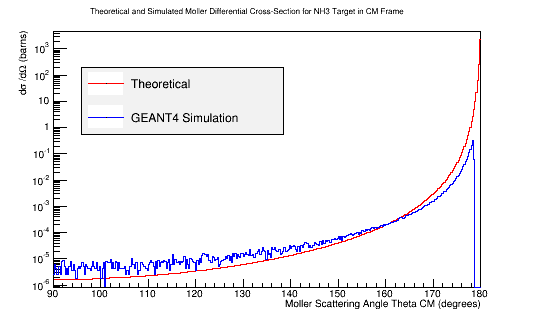
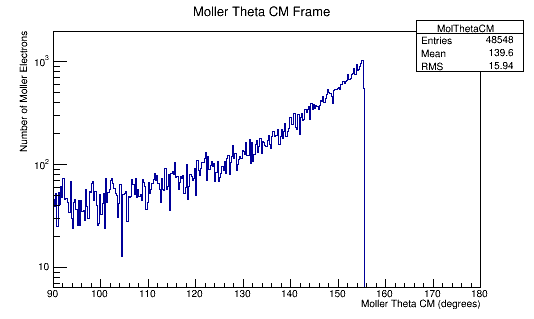
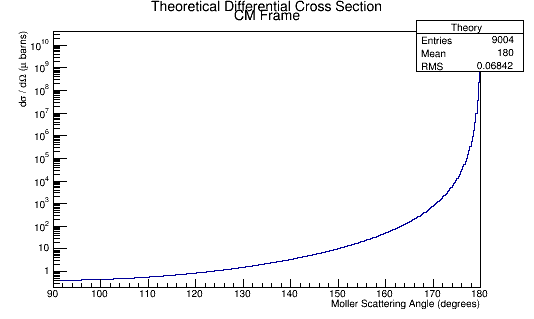
| + | [[File: MolThetaCM_E500Lab.png]][[File:NH3TheoryDiffXSect.png]] | ||
| − | |||
| + | Combining these plots, and rescaling the Final Theta in the Center of Mass for barns: | ||
| − | |||
| − | |||
| − | + | <pre> | |
| + | TH1F *Combo=new TH1F("TheoryExperiment","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180); | ||
| + | TH1F *Combo2=new TH1F("TheoryExperiment2","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180); | ||
| + | Combo->Add(MolThetaCM,8.87e-8); | ||
| + | Combo2->Add(Theory,1e-1); | ||
| + | Combo->Draw(); | ||
| + | Combo2->Draw("same"); | ||
| + | </pre> | ||
| − | <center>[[File: | + | <center>[[File:Adjusted_MollerXSect_NH3.png]]</center> |
Latest revision as of 21:03, 15 April 2016
Comparing experimental vs. theoretical for Møller differential cross section 11GeV
Using the equation from [1]
This can be simplified to the form
Plugging in the values expected for a scattering electron:
Using unit analysis on the term outside the parantheses, we find that the differential cross section for an electron at this momentum should be around
The trigonometric function part of the equation comes out to it's minimum of 9 at 90 degrees.
Using the conversion of
We find that the differential cross section scale is
Converting the number of electrons to barns,
where ρtarget is the density of the target material, ltarget is the length of the target, and iscattered is the number of incident particles scattered.
For a ammonia target,
Ammonia density:
Molecular weight calculation:
For 400 million incoming electrons
Combining these plots, and rescaling the Final Theta in the Center of Mass for barns:
TH1F *Combo=new TH1F("TheoryExperiment","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180);
TH1F *Combo2=new TH1F("TheoryExperiment2","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180);
Combo->Add(MolThetaCM,8.87e-8);
Combo2->Add(Theory,1e-1);
Combo->Draw();
Combo2->Draw("same");