Forest UCM MiNF

Mechanics in Noninertial Reference Frames

Linearly accelerating reference frames

Let [math]\mathcal S_0[/math] represent an inertial reference frame and \mathcal S represent an noninertial reference frame with acceleration [math]\vec A[/math] relative to [math]\mathcal S_0[/math].

Ball thrown straight up

Consider the motion of a ball thrown straight up as viewed from [math]\mathcal S[/math].

Using a Galilean transformation (not a relativistic Lorentz transformation)

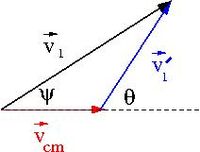
At some instant in time the velocities add like

[math]\dot {\vec {r}_0} = \dot {\vec r}+ \vec V[/math]

where

[math]\vec V[/math] = velocity of moving frame [math]\mathcal S[/math] with respect to [math]\mathcal S_0[/math] at some instant in time

[math]\Rightarrow \dot {\vec r} = \dot {\vec {r}_0} - \vec V[/math]

taking derivative with respect to time

[math]\Rightarrow \ddot {\vec r} = \ddot {\vec {r}_0} - \dot \vec V= \ddot {\vec {r}_0} - \vec A [/math]

[math]\Rightarrow m\ddot {\vec r} = m\ddot {\vec {r}_0} - m \vec A= \vec F - m\vec A= \vec F - \vec {F}_{\mbox {inertial}}[/math]

where

[math]\vec {F}_{\mbox {inertial}} = m \vec A \equiv[/math] inertial force

in your noninertial frame, the ball appears to have a force causing it to accelerate in the [math]\vec A[/math] direction.

The inertial force may also be referred to as a fictional force

an example is the "fictional" centrifugal force for rotational acceleration.

The observer in a noninertial reference frame will feel these frictional forces as if they are real but they are really a consequence of your accelerating reference frame

example

A force pushes you back into your seat when your Jet airplane takes off

you slam on the brakes and hit your head on the car's dashboard

Pedulum in an accelerating car

Consider a pendulum mounted inside a car that is accelerating to the right with a constant acceleration [math]\vec A[/math].

What is the pendulums equilibrium angle [math]\theta_0[/math]

In frame [math]\mathcal S_0[/math]

[math]\sum \vec F = m \ddot{\vec r_0}= \vec T + m \vec g[/math]

In frame [math]\mathcal S[/math]

[math]\sum \vec F = m \ddot{\vec r}= \vec T + m \vec g - m \vec A= \vec T + m \left ( \vec g -\vec A \right ) = \vec T + m \vec g_{eff} [/math]

If the pendulum is at rest and not oscillating then

[math]\sum \vec F = 0 = \vec T + m \vec g_{eff} [/math]

[math]g_{eff}[/math] is the vector sum of [math]g[/math] and [math]A[/math] which are orthogonal to each other in this problem thus

[math]\theta = tan^{-1}{\frac{g}{A}}[/math]

The pendulum oscillation frequency as seen in the accelerating car is

[math]\omega= \sqrt{\frac{g_{eff}}{l}} = \sqrt{\frac{\sqrt{g^2+A^2}}{l}}[/math]

Using lagrangian mechanics in the inertial frame

[math]\vec{r} = (l \sin \theta + \frac{1}{2} a t^2) \hat i + l \cos \theta \hat j[/math]

[math]\dot \vec{r} = (l \cos \theta \dot \theta + a t) \hat i + \sin \theta \dot \theta \hat j[/math]

[math] T = \frac{1}{2} mv^2 = \frac{1}{2} m \left ( (l \cos \theta \dot \theta + a t)^2 + \sin^2 \theta \dot \theta^2 \right )[/math]

[math]= \frac{1}{2} m \left ( l^2 \dot \theta^2 + 2 atl\dot \theta \cos \theta + a^2t^2\right )[/math]

[math]U =- mgy = -mgl \cos \theta[/math]

[math]\mathcal L = \frac{1}{2} m \left ( l^2 \dot \theta^2 + 2 atl\dot \theta \cos \theta + a^2t^2\right ) +mgl \cos \theta[/math]

[math] \left ( \frac{\partial \mathcal {L} }{\partial \theta} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \theta} \right ) [/math]

[math] -matl\sin \theta -mgl\sin \theta = \frac{d}{dt} \left ( ml^2\dot \theta + matl \cos \theta \right ) [/math]

[math] -at\sin \theta -g\sin \theta = l\ddot \theta - at \sin \theta \dot \theta + a \cos \theta[/math]

[math] l\ddot \theta=-g\sin \theta + a \cos \theta - at\sin \theta (1+ \dot \theta) [/math]

The tides

The gravitational force between the moon and the earth accelerates the earth and the ocean towards the moon.

The moon of mass [math](M_m)[/math] pulls on the earth of mass [math](M_e)[/math] such that

[math]\vec F = G \frac{M_m M_e}{d_0^3}\vec d_0 = M_e \vec A[/math]

where [math]d_0[/math] is the earth-moon distance of separation.

[math]\Rightarrow \vec A = G \frac{M_m }{d_0^3}\vec d_0 =[/math] Earth's acceleration towards the moon that makes the earth a non-inertial reference frame

The moon of mass [math](M_m)[/math] pulls on a test mass of water [math](M_o)[/math] on the surface of the earth's ocean such that

[math]\vec F = G \frac{M_m M_o}{d^3}\vec d[/math]

As seen in the Earth non-inertial reference frame

[math]M_o \ddot \vec r = \sum \vec F - M_o \vec A[/math]

= \left ( M_o \vec g + \vec F_N + G \frac{M_m M_o}{d^3}\vec d \right ) - G \frac{M_m }{d_0^3}\vec d_0 \vec A

where

[math]\vec F_N =[/math] a net non-graviational force hold the mass M_o in top of the ocean (Bouyant force)

[math]M_o \ddot \vec r = \left ( M_o \vec g + \vec F_N + G \frac{M_m M_o}{d^3}\vec d \right ) - G \frac{M_m }{d_0^3}\vec d_0 \vec A :: \lt math\gt = M_o \vec g + \vec F_N + \vec{F}_{\mbox{tide}}[/math]

Forest_Ugrad_ClassicalMechanics