Forest UCM MiNF

Mechanics in Noninertial Reference Frames

Linearly accelerating reference frames

Let [math]\mathcal S_0[/math] represent an inertial reference frame and \mathcal S represent an noninertial reference frame with acceleration [math]\vec A[/math] relative to [math]\mathcal S_0[/math].

Ball thrown straight up

Consider the motion of a ball thrown straight up as viewed from [math]\mathcal S[/math].

Using a Galilean transformation (not a relativistic Lorentz transformation)

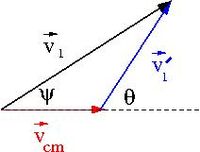
At some instant in time the velocities add like

[math]\dot {\vec {r}_0} = \dot {\vec r}+ \vec V[/math]

where

[math]\vec V[/math] = velocity of moving frame [math]\mathcal S[/math] with respect to [math]\mathcal S_0[/math] at some instant in time

[math]\Rightarrow \dot {\vec r} = \dot {\vec {r}_0} - \vec V[/math]

taking derivative with respect to time

[math]\Rightarrow \ddot {\vec r} = \ddot {\vec {r}_0} - \dot \vec V= \ddot {\vec {r}_0} - \vec A[/math]

Forest_Ugrad_ClassicalMechanics