Difference between revisions of "Forest UCM CoV"
| (248 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
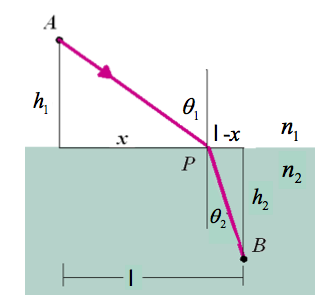
| − | Fermats principle is | + | Fermats principle is that light takes a path between two points that requires the least amount of time. |
| + | |||
| + | [[File:TF_Fermat_LawSines.png|| 400 px]] | ||
If we let S represent the path of light between two points then | If we let S represent the path of light between two points then | ||
| Line 29: | Line 31: | ||
::<math>= \frac{n_1}{c}\int_A^I ds+ \frac{n_2}{c} \int_I^B ds </math> | ::<math>= \frac{n_1}{c}\int_A^I ds+ \frac{n_2}{c} \int_I^B ds </math> | ||
::<math>= \frac{n_1}{c}\sqrt{h_1^2 + x^2}+ \frac{n_2}{c} \sqrt{h_2^2 + (\ell -x)^2} </math> | ::<math>= \frac{n_1}{c}\sqrt{h_1^2 + x^2}+ \frac{n_2}{c} \sqrt{h_2^2 + (\ell -x)^2} </math> | ||
| + | |||
| + | take derivative of time with respect to <math>x</math> to find a minimum for the time of flight | ||
| + | |||
| + | :<math> \frac{d t}{dx} = 0</math> | ||
| + | :<math> \Rightarrow 0 = \frac{d}{dx} \left ( \frac{n_1}{c}\left ( h_1^2 + x^2 \right )^{\frac{1}{2}}+ \frac{n_2}{c} \left (h_2^2 + (\ell -x)^2 \right)^{\frac{1}{2}} \right )</math> | ||
| + | ::<math> = \frac{n_1}{c}\left( h_1^2 + x^2 \right )^{\frac{-1}{2}} (2x) + \frac{n_2}{c} \left (h_2^2 + (\ell -x)^2 \right)^{\frac{-1}{2}} 2(\ell -x)(-1)</math> | ||
| + | ::<math> = \frac{n_1}{c}\frac{x}{\sqrt{ h_1^2 + x^2 }} + \frac{n_2}{c} \frac{(\ell -x)(-1)}{\sqrt{h_2^2 + (\ell -x)^2}} </math> | ||
| + | ::<math> = n_1\frac{x}{\sqrt{ h_1^2 + x^2 }} - n_2 \frac{\ell -x}{\sqrt{h_2^2 + (\ell -x)^2}} </math> | ||
| + | :<math> \Rightarrow n_1\frac{x}{\sqrt{ h_1^2 + x^2 }} = n_2 \frac{\ell -x}{\sqrt{h_2^2 + (\ell -x)^2}} </math> | ||
| + | |||
| + | or | ||
| + | |||
| + | :<math> \Rightarrow n_1\sin(\theta_1) = n_2 \sin(\theta_2) </math> | ||
| + | |||
| + | ==Generalizing Fermat's principle to determining the shorest path== | ||
| + | |||
| + | One can apply Fermat's principle to show that the shortest path between two points is a straight line. | ||
| + | |||
| + | In 2-D one can write the differential path length as | ||
| + | |||
| + | :<math>ds=\sqrt{dx^2+dy^2}</math> | ||
| + | |||
| + | using chain rule | ||
| + | |||
| + | :<math>dy = \frac{dy}{dx} dx \equiv y^{\prime}(x) dx</math> | ||
| + | |||
| + | the the path length between two points <math>(x_1,y_1)</math> and <math>(x_2,y_2)</math> is | ||
| + | |||
| + | :<math>S = \int_{(x_1,y_1)}^{(x_2,y_2)} ds= \int_{(x_1,y_1)}^{(x_2,y_2)} \sqrt{dx^2+dy^2}</math> | ||
| + | ::<math> = \int_{(x_1,y_1)}^{(x_2,y_2)} \sqrt{dx^2+\left ( y^{\prime}(x) dx\right)^2}</math> | ||
| + | ::<math> = \int_{(x_1,y_1)}^{(x_2,y_2)} \sqrt{1+y^{\prime}(x)^2}dx</math> | ||
| + | |||
| + | adding up the minimum of the integrand function is one way to minimize the integral ( or path length) | ||
| + | |||
| + | let | ||
| + | |||
| + | :<math>f(y,y^{\prime};x) \equiv \sqrt{1+y^{\prime}(x)^2}</math> | ||
| + | |||
| + | ;Note: in the above <math>x</math> is the independent variable in the function while <math>y</math> and <math>y^{\prime}</math> depend on <math>x</math>. The semicolon is used to separate them with the independent variable appearing last | ||
| + | |||
| + | the path integral can now be written in terms of dx such that | ||
| + | |||
| + | :<math>S= \int_{(x_1)}^{(x_2)} f(y,y^{\prime},x) dx</math> | ||
| + | |||
| + | |||
| + | To consider deviation away from <math>y(x)</math> the function <math>\eta(x)</math> is introduced to denote deviations away from the shortest line and the parameter <math>\alpha</math> is introduced to weight that deviation | ||
| + | |||
| + | :<math>\eta(x)</math> = the difference between the current curve and the shortest path. | ||
| + | |||
| + | let | ||
| + | |||
| + | :<math>Y(x) = y(x) + \alpha \eta(x)</math> = A path that is not the shortest path between two points. | ||
| + | |||
| + | |||
| + | ;Note | ||
| + | :It is stipulated that <math>\eta(x)</math> is independent of <math>\alpha</math> to ensure that in the <math>\alpha \rightarrow 0</math> limit, <math>Y(x) = y(x)</math> and <math>Y^{\prime}(x) = y^{\prime}(x)</math> | ||
| + | : ie; both the function <math>Y</math> and its derivative approach <math>y(x)</math> | ||
| + | |||
| + | let | ||
| + | |||
| + | :<math>S(\alpha)= \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx</math> | ||
| + | :<math>= \int_{(x_1)}^{(x_2)} f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) dx</math> | ||
| + | |||
| + | the deviations in the various paths can be expressed in terms of a differential of the above integral for the path length with respect to the parameter <math>\alpha</math> as this parameter changes the deviation | ||
| + | :<math>\frac{\partial}{\partial \alpha} f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) = \frac{\partial y}{\partial \alpha}\frac{\partial f}{\partial y}+\frac{\partial y^{\prime}}{\partial \alpha} \frac{\partial f}{\partial y^{\prime}}= \eta \frac{\partial f}{\partial y}+\eta^{\prime} \frac{\partial f}{\partial y^{\prime}}</math> | ||
| + | |||
| + | |||
| + | :<math>\frac{dS(\alpha)}{d \alpha}=\frac{d}{d \alpha} \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx</math> | ||
| + | ::<math>= \int_{(x_1)}^{(x_2)} \frac{d}{d \alpha}f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) dx</math> | ||
| + | ::<math>= \int_{(x_1)}^{(x_2)} \left ( \eta \frac{\partial f}{\partial y}+\eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx</math> | ||
| + | ::<math>= \int_{(x_1)}^{(x_2)} \left ( \eta \frac{\partial f}{\partial y} \right ) + \int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx</math> | ||
| + | |||
| + | |||
| + | The second integral above can by evaluated using integration by parts as | ||
| + | |||
| + | let | ||
| + | |||
| + | : <math>u = \frac{\partial f}{\partial y^{\prime}} \;\;\;\;\;\;\;\;\;\;\;\; dv = \eta^{\prime} dx</math> | ||
| + | : <math>du = \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \;\;\;\;\;\;\;\;\;\;\;\; v=\eta </math> | ||
| + | |||
| + | ::<math>\int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx = \left [ \eta \frac{\partial f}{\partial y^{\prime}} \right ]_{x_1}^{x_2} - \int_{(x_1)}^{(x_2)} \eta \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right )dx </math> | ||
| + | |||
| + | |||
| + | |||
| + | :<math>\left [ \eta \frac{\partial f}{\partial y^{\prime}} \right ]_{x_1}^{x_2} = \left [ \eta \frac{y^{\prime}(x)}{ \sqrt{1+y^{\prime}(x)^2} } \right ]_{x_1}^{x_2} </math> :<math>f(y,y^{\prime},x) \equiv \sqrt{1+y^{\prime}(x)^2}</math> | ||
| + | ::<math>= \left ( \eta(x_2) - \eta(x_1) \right ) \frac{y^{\prime}(x)}{ \sqrt{1+y^{\prime}(x)^2}} </math> | ||
| + | |||
| + | : the difference between the end points should be zero because <math>\eta(x_1) = \eta(x_2)</math> to keep be sure that the endpoints are the same | ||
| + | |||
| + | |||
| + | ::<math>\int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx = 0 - \int_{(x_1)}^{(x_2)} \eta \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right )dx </math> | ||
| + | |||
| + | |||
| + | |||
| + | :<math>\frac{dS(\alpha)}{d \alpha}=\frac{d}{d \alpha} \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx</math> | ||
| + | ::<math>= \int_{(x_1)}^{(x_2)} \left ( \eta \frac{\partial f}{\partial y} \right ) - \int_{(x_1)}^{(x_2)} \eta \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right )dx </math> | ||
| + | ::<math>= \int_{(x_1)}^{(x_2)} \eta \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] dx </math> | ||
| + | |||
| + | |||
| + | The above integral is equivalent to | ||
| + | |||
| + | :<math>\int \eta(x) g(x) = 0</math> | ||
| + | |||
| + | |||
| + | For the above to be true for any function <math>\eta(x)</math> then it follows that <math>g(x)</math> should be zero | ||
| + | |||
| + | |||
| + | ::<math> \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] =0 </math> | ||
| + | |||
| + | |||
| + | :<math>f(y,y^{\prime},x) \equiv \sqrt{1+y^{\prime}(x)^2}</math> | ||
| + | |||
| + | |||
| + | :<math>\frac{\partial f}{\partial y} = \frac{\partial }{\partial y} \sqrt{1+y^{\prime}(x)^2} = 0 </math> | ||
| + | |||
| + | :<math> \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) = \frac{d}{dx} \left ( \frac{\partial ( \sqrt{1+y^{\prime}(x)^2})}{\partial y^{\prime}} \right ) = \frac{\partial f}{\partial y} = 0 </math> | ||
| + | :<math> \Rightarrow \left ( \frac{\partial ( \sqrt{1+y^{\prime}(x)^2})}{\partial y^{\prime}} \right ) </math>= Constant | ||
| + | :<math> \frac{y^{\prime}(x)}{ \sqrt{1+y^{\prime}(x)^2}} = C </math> | ||
| + | :<math> \left ( y^{\prime}(x)\right )^2=C^2 \left ( 1+y^{\prime}(x)^2\right ) </math> | ||
| + | :<math> \left (1 - C^2 \right ) \left ( y^{\prime(x) }\right )^2=C^2 </math> | ||
| + | :<math> \left ( y^{\prime}(x)\right )^2=\frac{C^2}{1 - C^2) } </math> | ||
| + | :<math> y^{\prime}(x)=\sqrt{\frac{C^2}{1 - C^2) } } \equiv m</math> | ||
| + | integrating | ||
| + | |||
| + | : <math>y =mx+b</math> | ||
| Line 36: | Line 163: | ||
== Euler-Lagrange Equation== | == Euler-Lagrange Equation== | ||
| + | The Euler- Lagrange Equation is written as | ||
| + | |||
| + | :<math> \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] =0 </math> | ||
| + | |||
| + | |||
| + | the above becomes a condition for minimizing the "Action" | ||
| + | |||
| + | ==Shortest distance betwen two points revisited== | ||
| + | |||
| + | Let's consider the problem of determining the shortest distance between two points again. | ||
| + | |||
| + | Previously we determined the shortest distance by assuming only two variables. One was the independent variable <math>x</math> and the other, (<math> y(x)</math>), was dependent on <math>x</math> . | ||
| + | |||
| + | |||
| + | What happens if the above assumption is relaxed. | ||
| + | |||
| + | To consider all possible paths between two point we should write the path in parameteric form | ||
| + | |||
| + | :<math> x=x(u) \;\;\;\;\;\; y = y(u)</math> | ||
| + | |||
| + | The functions above are assumed to be continuous and have continuous second derivatives. | ||
| + | |||
| + | ;Note: the above parameterization includes our previous assumption of the variables if we just let <math>u=x</math>. | ||
| + | |||
| + | ;Other examples | ||
| + | |||
| + | :<math> x=u \;\;\;\;\;\; y = u^2 \;\;\;\;\ \Rightarrow y = x^2 =</math> parabola | ||
| + | :<math> x=\sin u \;\;\;\;\;\; y = \cos u \;\;\;\;\ \Rightarrow x^2 + y^2 =1 =</math>circle | ||
| + | :<math> x=a\sin u \;\;\;\;\;\; y = b\cos u \;\;\;\;\ \Rightarrow </math>ellips | ||
| + | :<math> x=a\sec u \;\;\;\;\;\; y = b\tan u \;\;\;\;\ \Rightarrow </math>hyperbola | ||
| + | |||
| + | The length of a small segment of the path is given by | ||
| + | |||
| + | |||
| + | :<math>ds = \sqrt{dx^2 + dy^2}= \sqrt{x^{\prime}(u)^2 + y^{\prime}(u)^2}</math> | ||
| + | |||
| + | |||
| + | |||
| + | now instead of | ||
| + | |||
| + | :<math>f(y,y^{\prime},x) \equiv \sqrt{1+y^{\prime}(x)^2}</math> | ||
| + | |||
| + | you have | ||
| + | |||
| + | : <math>f(x(u),y(u),x^{\prime}(u),y^{\prime}(u),u) \equiv \sqrt{x^{\prime}(u)^2 + y^{\prime}(u)^2} </math> | ||
| + | |||
| + | and the path integral changes from | ||
| + | |||
| + | :<math>S= \int_{(x_1)}^{(x_2)} f(y,y^{\prime},x) dx</math> | ||
| + | |||
| + | to | ||
| + | |||
| + | |||
| + | : <math>L = \int_{u_1}^{u_2} \sqrt{x^{\prime}(u)^2 + y^{\prime}(u)^2} du =\int_{u_1}^{u_2} f(x(u),y(u),x^{\prime}(u),y^{\prime}(u),u)du</math> | ||
| + | |||
| + | |||
| + | the same arguments are made again | ||
| + | |||
| + | instead of | ||
| + | |||
| + | |||
| + | :<math>Y(x) = y(x) + \alpha \eta(x)</math> | ||
| + | |||
| + | |||
| + | You now have | ||
| + | |||
| + | |||
| + | |||
| + | :<math> y = y(u) + \alpha \eta(u) \;\;\;\;\;\;\;\; x(u) + \beta \xi(u) </math> | ||
| + | |||
| + | |||
| + | |||
| + | instead of | ||
| + | |||
| + | :<math>S(\alpha)= \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx</math> | ||
| + | :<math>= \int_{(x_1)}^{(x_2)} f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) dx</math> | ||
| + | |||
| + | |||
| + | you now have | ||
| + | |||
| + | :<math>S(\alpha,\beta)= \int_{(u_1)}^{(u_2)} f(x(u),y(u),x^{\prime}(u),y^{\prime}(u),u)du</math> | ||
| + | :<math>= \int_{(u_1)}^{(u_2)} f(x(u) + \beta \xi(u),x^{\prime}(u) + \beta \xi^{\prime}(u),y(u)+\alpha \eta(u),y^{\prime}(u)+ \alpha \eta^{\prime}(u),u) du</math> | ||
| + | |||
| + | |||
| + | If you require that the integral not deviate from the shortest path between two points (i.e. it is stationary) | ||
| + | Then you are requiring that the integral from path segments that deviate from the shortest path satisfies the equation | ||
| + | |||
| + | : <math>\frac{\partial S}{\partial \alpha} = 0\;\;\;\;</math> and <math>\;\;\;\;\;\frac{\partial S}{\partial \beta} = 0</math> | ||
| + | |||
| + | when | ||
| + | |||
| + | :<math>\alpha \mbox{and} \beta = 0</math> for any function <math>\eta(u)</math> and <math>\xi(u)</math> that vanish at the endpoints <math>u_1</math> and <math>u_2</math> | ||
| + | |||
| + | :<math>\frac{\partial S(\alpha)}{\partial \alpha}=\frac{\partial}{\partial \alpha} \int_{(u_1)}^{(u_2)} f(x(u) + \beta \xi(u),x^{\prime}(u) + \beta \xi^{\prime}(u),y(u)+\alpha \eta(u),y^{\prime}(u)+ \alpha \eta^{\prime}(u),u) du</math> | ||
| + | ::<math>= \int_{(u_1)}^{(u_2)} \left ( \eta \frac{\partial f}{\partial y}+\eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx</math> | ||
| + | ::<math>= \int_{(u_1)}^{(u_2)} \left ( \eta \frac{\partial f}{\partial y} \right ) + \int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )du</math> | ||
| + | ::<math>= \int_{(u_1)}^{(u_2)} \left ( \eta \frac{\partial f}{\partial y} \right ) - \int_{(x_1)}^{(x_2)} \eta \frac{d}{du} \left ( \frac{\partial f}{\partial y^{\prime}} \right )du </math> | ||
| + | ::<math>= \int_{(u_1)}^{(u_2)} \eta \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{du} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] du </math> | ||
| + | |||
| + | |||
| + | |||
| + | or | ||
| + | |||
| + | |||
| + | ::<math> \frac{\partial f}{\partial y} = \frac{d}{du} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) </math> | ||
| + | |||
| + | |||
| + | similarly | ||
| + | |||
| + | ::<math> \frac{\partial f}{\partial x} = \frac{d}{du} \left ( \frac{\partial f}{\partial x^{\prime}} \right ) </math> | ||
| + | |||
| + | ===Apply Euler-Lagrange to shortest path problem revisited=== | ||
| + | |||
| + | |||
| + | :<math>f(x,x^{\prime},y,y^{\prime},u) = \sqrt{x^{\prime\;2}+y^{\prime\;2}}</math> | ||
| + | |||
| + | :<math>\frac{\partial f}{\partial x} = 0 = \frac{d}{du} \frac{\partial f}{\partial x^{\prime}}</math> | ||
| + | |||
| + | |||
| + | :<math>\Rightarrow \frac{ \partial f}{\partial x^{\prime}} = C_1</math>= constant | ||
| + | ::<math>= \frac{x^{\prime}}{\sqrt{x^{\prime\;2}+x^{\prime\;2}}}</math> | ||
| + | |||
| + | similarly | ||
| + | |||
| + | ::<math>C_2= \frac{y^{\prime}}{\sqrt{x^{\prime\;2}+y^{\prime\;2}}}</math> | ||
| + | |||
| + | |||
| + | ::<math>\frac{C_2}{C_1} = \frac{ \frac{y^{\prime}}{\sqrt{x^{\prime\;2}+y^{\prime\;2}}}}{\frac{x^{\prime}}{\sqrt{x^{\prime\;2}+x^{\prime\;2}}}}= \frac{ y^{\prime}}{x^{\prime}} \equiv m</math> | ||
| + | |||
| + | ===Shortest path along a sphere=== | ||
| + | |||
| + | :<math>ds = \sqrt{(Rd\theta)^2+(R\sin \theta d\phi)^2}= R\sqrt{1+\sin^2 \theta \phi ^{\prime\;2(\theta)}} d\theta</math> | ||
| + | |||
| + | :<math>S=\int_{\theta_1}{\theta_2} R\sqrt{1+\sin^2 \theta \phi ^{\prime\;2}(\theta)} d\theta</math> | ||
| + | |||
| + | :<math>f(\phi,\phi^{\prime},\theta) =R\sqrt{1+\sin^2 \theta \phi^{\prime\;2}(\theta)} </math> | ||
| + | |||
| + | :<math>\frac{\partial f}{\partial \phi} = 0 = \frac{d}{d\theta} \frac{\partial f}{\partial \phi^{\prime}}</math> | ||
| + | |||
| + | |||
| + | :<math>\Rightarrow \frac{\partial f}{\partial \phi^{\prime}} = C</math>= constant | ||
| + | ::<math>= \frac{\sin^2 \theta \phi^{\prime}}{\sqrt{1+\sin^2 \theta \phi^{\prime\;2}}}</math> | ||
| + | |||
| + | Assume the location of the first point is at <math>\theta_1=0</math> </math> | ||
| + | |||
| + | :<math> C=0 = \frac{\sin^2 \theta_1 \phi^{\prime}}{\sqrt{1+\sin^2 \theta_1 \phi^{\prime\;2}}}</math> | ||
| + | ::<math>\Rightarrow \phi^{\prime} = 0</math> | ||
| + | ::<math>\Rightarrow \phi = Constant</math> | ||
| + | |||
| + | The curves of constant <math>\phi</math> are lines of longitude and are great circles which are geodesics (the shortest lines between two points on a shphere) | ||
| + | |||
| + | |||
| + | ===Brachystochrone problem=== | ||
| + | |||
| + | In the brachystochrone (Greek for "shortest time") problem we are determining the path of a bead between two points that takes the shortest time when the bead is constrained to slide along a wire without friction and in the presence of gravity. | ||
| + | |||
| + | |||
| + | The fall time for the bead is given by | ||
| + | |||
| + | :<math>t=\frac{d}{v}</math> | ||
| + | |||
| + | Using conservation of energy one may cast the beads velocity as | ||
| + | |||
| + | :<math> \frac{1}{2} m v^2 = mgy \Rightarrow v = \sqrt{2gy}</math> | ||
| + | |||
| + | : <math>\Rightarrow t = \frac{d}{\sqrt{2gy}}</math> | ||
| + | |||
| + | This problem is similar to the shortest distance between two points problem above in that one can write the time variation that you wish to minimize in terms of the path variation | ||
| + | |||
| + | :<math>ds = \sqrt{dx^2 + dy^2} </math> | ||
| + | |||
| + | This time however there is an external driving force which is a function of the distance <math>y</math>. So instead of writing the distance variation <math>ds</math> as a function of <math>dx</math> with <math>y(x)</math> we will want to write it as a function of <math>dy</math> with <math>x(y)</math> | ||
| + | |||
| + | :<math>ds = \sqrt{(x^{\prime}(y))^2+ 1 }dy </math> | ||
| + | |||
| + | then | ||
| + | |||
| + | :<math>t = \int \frac{ds}{v} = \int \left ( \frac{(x^{\prime}(y))^2+ 1 }{2gy}\right )^{\frac{1}{2}} dy</math> | ||
| + | |||
| + | :<math> \Rightarrow f(x,x^{\prime},y) = \left ( \frac{(x^{\prime}(y))^2+ 1 }{y}\right )^{\frac{1}{2}} </math> | ||
| + | |||
| + | since<math> f</math> is an explicit function of <math>y</math> and | ||
| + | |||
| + | :<math>\frac{\partial f}{\partial x} = 0</math> | ||
| + | |||
| + | then we can use the Euler-Lagrange equation | ||
| + | |||
| + | :<math> \left [ \left ( \frac{\partial f}{\partial x} \right ) - \frac{d}{dy} \left ( \frac{\partial f}{\partial x^{\prime}} \right ) \right ] =0 </math> | ||
| + | |||
| + | ;Notice how the variables x & y have been interchanged now that <math>x</math> is written as a function of<math> y (x^{\prime}(y))</math> whereas before <math>y</math> was written as a function of <math>x (y^{\prime}(x))</math> | ||
| + | |||
| + | :<math> \left [ \left ( \frac{\partial f}{\partial x} \right ) =0= \frac{d}{dy} \left ( \frac{\partial f}{\partial x^{\prime}} \right ) \right ] </math> | ||
| + | :<math>\Rightarrow \left ( \frac{\partial f}{\partial x^{\prime}} \right ) =</math>constant | ||
| + | |||
| + | :<math> \frac{\partial f}{\partial x^{\prime}} = \frac{\partial }{\partial x^{\prime}}\left ( \frac{(x^{\prime}(y))^2+ 1 }{y}\right )^{\frac{1}{2}} </math> | ||
| + | ::<math> = \frac{1}{\sqrt y} \left ( (x^{\prime}(y))^2+ 1 \right )^{\frac{-1}{2}}x^{\prime}(y)</math> | ||
| + | ::<math> = \frac{x^{\prime}(y)}{\sqrt {y(1+(x^{\prime}(y))^2)}} </math> = constant | ||
| + | |||
| + | or | ||
| + | |||
| + | ::<math>\frac{(x^{\prime}(y))^2}{y(1+(x^{\prime}(y))^2)} </math> = constant | ||
| + | |||
| + | ;using the foresight of working this problem before , the convenient constant is defined as | ||
| + | |||
| + | ::<math>\frac{(x^{\prime}(y))^2}{y(1+(x^{\prime}(y))^2)} = \frac{1}{2a} </math> | ||
| + | ::<math>(x^{\prime}(y))^2=\frac{y(1+(x^{\prime}(y))^2)}{2a} </math> | ||
| + | ::<math>(x^{\prime}(y))^2 (2a-y)=y </math> | ||
| + | ::<math>(x^{\prime}(y))=\frac{dx}{dy} = \left ( \frac{y}{2a-y} \right )^{\frac{1}{2}}</math> | ||
| + | |||
| + | |||
| + | :<math>dx = \left ( \frac{1}{y(2a-y)}\right )^\frac{1}{2} ydy</math> | ||
| + | |||
| + | :<math>\Rightarrow \int dx = \int \left ( \frac{1}{y(2a-y)}\right )^{\frac{1}{2}} ydy</math> | ||
| + | |||
| + | let | ||
| + | <math>y = a(1 - \cos \theta)</math> | ||
| + | <math>dy = a \sin \theta d \theta</math> | ||
| + | |||
| + | :<math>\Rightarrow \int dx = \int \left ( \frac{1}{a(1 - \cos \theta)(2a-1+\cos \theta)}\right )^{\frac{1}{2}} a(1 - \cos \theta)a \sin \theta d \theta</math> | ||
| + | ::<math> = \int \left ( \frac{1}{a^2(1 - \cos \theta)(1+\cos \theta)}\right )^{\frac{1}{2}} a(1 - \cos \theta)a \sin \theta d \theta</math> | ||
| + | ::<math> = \int \left ( \frac{1}{a^2(1 - \cos^2 \theta)}\right )^{\frac{1}{2}} a(1 - \cos \theta)a \sin \theta d \theta</math> | ||
| + | ::<math> = \int \left ( \frac{1}{a^2 \sin^2 \theta}\right )^{\frac{1}{2}} a(1 - \cos \theta)a \sin \theta d \theta</math> | ||
| + | ::<math> = \int a(1 - \cos \theta) d \theta</math> | ||
| + | |||
| + | :<math> x = a(\theta - \sin \theta) + constant</math> | ||
| + | |||
| + | returning to the substitution used for integration we have | ||
| + | |||
| + | <math>dy = a \sin \theta d \theta</math> | ||
| + | <math>y = a \int \sin \theta d \theta</math> | ||
| + | :<math> = -a \cos \theta + constant</math> | ||
| + | |||
| + | ==alternate form of Euler-Lagrange equation== | ||
| + | |||
| + | ===Brachistochrone problem revisited=== | ||
| + | |||
| + | Consider the Brachistochrone problem again but this time do not cast <math>x^{\prime}</math> as a function of <math>y</math> | ||
| + | |||
| + | |||
| + | The fall time for the bead is given by | ||
| + | |||
| + | :<math>t=\frac{d}{v}</math> | ||
| + | |||
| + | Using conservation of energy one may cast the beads velocity as | ||
| + | |||
| + | :<math> \frac{1}{2} m v^2 = mgy \Rightarrow v = \sqrt{2gy}</math> | ||
| + | |||
| + | : <math>\Rightarrow t = \frac{d}{\sqrt{2gy}}</math> | ||
| + | |||
| + | This problem is similar to the shortest distance between two points problem above in that one can write the time variation that you wish to minimize in terms of the path variation | ||
| + | |||
| + | :<math>ds = \sqrt{dx^2 + dy^2} </math> | ||
| + | |||
| + | :<math>ds = \sqrt{1 + (y^{\prime}(x))^2}dx </math> | ||
| + | |||
| + | then | ||
| + | |||
| + | :<math>t = \int \frac{ds}{v} = \int \left (\frac{1 + (y^{\prime}(x))^2}{2gy}\right )^{\frac{1}{2}} dx</math> | ||
| + | |||
| + | :<math> \Rightarrow f(y(x),y^{\prime}(x);x) = \left ( \frac{(x^{\prime}(y))^2+ 1 }{y}\right )^{\frac{1}{2}} </math> | ||
| + | |||
| + | ;BUT the above function appears to be independent of x and | ||
| + | |||
| + | ::<math>\frac{\partial f }{\partial y} \ne 0</math> | ||
| + | |||
| + | === alternate form of Euler-Lagrange's equation (the first integral) === | ||
| + | |||
| + | In the previous problems of finding the shortest distance between two point in 2-D and 2 point on the surface of the sphere, the extreme function <math>f</math> was independent of <math>x</math> (or <math>\phi</math>) | ||
| + | |||
| + | for the 2-D line | ||
| + | :<math>f(y(x),y^{\prime}(x),x) \equiv \sqrt{1+y^{\prime}(x)^2}\;\;\;\;\frac{ \partial f}{\partial y} = 0</math> | ||
| + | |||
| + | for the geodesic | ||
| + | :<math>f(\phi(\theta),\phi^{\prime}(\theta) ,\theta) =R\sqrt{1+\sin^2 \theta \phi^{\prime\;2}(\theta)}\;\;\;\;\frac{ \partial f}{\partial \phi} = 0</math> | ||
| + | |||
| + | there are some problems where the functional dependence of <math>f</math> on <math> x</math> or <math>\theta</math> is not explicit | ||
| + | |||
| + | because of this we need to use the chain to take the total derivative of the function <math>f(y,y^{\prime},x)</math> with respect to <math>x</math> | ||
| + | |||
| + | :<math>\frac{d f}{dx} = \frac{d}{dx} \left [ f(y(x),y^{\prime}(x),x) \right ]</math> | ||
| + | ::<math>= \frac{\partial f}{\partial y}\frac{\partial y}{\partial x} + \frac{\partial f}{\partial y^{\prime}}\frac{\partial y^{\prime}}{\partial x}+\frac{\partial f}{\partial x} </math> | ||
| + | ::<math>= \frac{\partial y}{\partial x}\frac{\partial f}{\partial y} + \frac{\partial y^{\prime}}{\partial x}\frac{\partial f}{\partial y^{\prime}} +\frac{\partial f}{\partial x} </math> | ||
| + | ::<math>= \left ( y^{\prime}\right ) \frac{\partial f}{\partial y} + \left ( y^{\prime\prime}\right ) \frac{\partial f}{\partial y^{\prime}} +\frac{\partial f}{\partial x} </math> | ||
| + | |||
| + | ;Notice | ||
| + | :<math>\frac{d}{dx} \left [ y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ] =\frac{\partial y^{\prime}}{\partial x} \frac{\partial f}{\partial y^{\prime}} + y^{\prime}\frac{d}{dx} \left [ \frac{\partial f}{\partial y^{\prime} }\right ]</math> | ||
| + | ::<math> =\left ( y^{\prime\prime}\right ) \frac{\partial f}{\partial y^{\prime}} + y^{\prime}\frac{d}{dx} \left [ \frac{\partial f}{\partial y^{\prime} }\right ]</math> | ||
| + | ::<math> \Rightarrow \left ( y^{\prime\prime}\right ) \frac{\partial f}{\partial y^{\prime}} =\frac{d}{dx} \left [ y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ]- y^{\prime}\frac{d}{dx} \left [ \frac{\partial f}{\partial y^{\prime} }\right ]</math> | ||
| + | |||
| + | |||
| + | substitution in for<math> y^{\prime\prime}</math> and moving terms around | ||
| + | |||
| + | :<math>\frac{d f}{dx} = \left ( y^{\prime}\right ) \frac{\partial f}{\partial y} + \left ( \frac{d}{dx} \left [ y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ]- y^{\prime}\frac{d}{dx} \left [ \frac{\partial f}{\partial y^{\prime} }\right ]\right ) +\frac{\partial f}{\partial x} </math> | ||
| + | |||
| + | |||
| + | : <math>\Rightarrow\frac{d f}{dx} - \left ( y^{\prime}\right ) \frac{\partial f}{\partial y} - \left ( \frac{d}{dx} \left [ y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ]+ y^{\prime}\frac{d}{dx} \left [ \frac{\partial f}{\partial y^{\prime} }\right ]\right ) -\frac{\partial f}{\partial x}=0</math> | ||
| + | |||
| + | rearranging | ||
| + | |||
| + | : <math>\frac{d f}{dx} -\frac{\partial f}{\partial x} - \frac{d}{dx} \left [ y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ] - y^{\prime}\left (\frac{\partial f}{\partial y} -\frac{d}{dx} \left [ \frac{\partial f}{\partial y^{\prime} }\right ]\right ) =0</math> | ||
| + | |||
| + | Euler-Lagrange Equation | ||
| + | : <math>\left (\frac{\partial f}{\partial y} -\frac{d}{dx} \left [ \frac{\partial f}{\partial y^{\prime} }\right ]\right ) =0</math> | ||
| + | |||
| + | Then the alternate form of Euler-Lagrange's equation is | ||
| + | |||
| + | : <math> \frac{\partial f}{\partial x} - \frac{d }{dx} \left [f- y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ] =0</math> | ||
| + | |||
| + | === returning to Brachistochrone === | ||
| + | |||
| + | Returning back the the brachistochrone problem | ||
| + | |||
| + | |||
| + | :<math> f(y(x),y^{\prime}(x),x) = \left ( \frac{1+(y^{\prime}(x))^2 }{y}\right )^{\frac{1}{2}} </math> | ||
| + | |||
| + | ;Since the above function appears to be independent of x and | ||
| + | |||
| + | ::<math>\frac{\partial f }{\partial y} \ne 0</math> | ||
| + | |||
| + | the alternate form of Euler-Lagrange's equation (the first integral) is used | ||
| + | |||
| + | : <math> \frac{\partial f}{\partial x} - \frac{d }{dx} \left [f- y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ] =0</math> | ||
| + | |||
| + | |||
| + | ::<math>\frac{\partial f }{\partial x} = 0 \Rightarrow \left [f- y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ] =</math>constant | ||
| + | |||
| + | :<math>\left [f- y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ] = \left ( \frac{1+(y^{\prime}(x))^2 }{y}\right )^{\frac{1}{2}} - \frac{y^{\prime}}{y}\left( \frac{(y^{\prime}(x))^2 }{1+(y^{\prime}(x))^2}\right )^{\frac{1}{2}}=2R</math> | ||
| + | |||
| + | |||
| + | :<math>y(1+(y^{\prime})^2) = 2R</math> | ||
| + | |||
| + | let | ||
| + | |||
| + | :<math>y^{\prime}= \cot (\theta/2)</math> | ||
| + | |||
| + | substituting | ||
| + | |||
| + | : <math>y = \frac{2R}{1+\frac{\cos^2 (\theta/2)}{\sin^2(\theta/2)}} =2R \sin^2 \left ( \frac{\theta}{2} \right ) = 2R ( 1 - \cos \theta)</math> | ||
| + | |||
| + | to find <math>x</math> just return to definition of <math>y^{\prime}</math> | ||
| + | |||
| + | :<math>y^{\prime}= \frac{d y}{dx} = \cot (\theta/2)</math> | ||
| + | |||
| + | :<math>dx= dy \tan (\theta/2) = d(2R ( 1 - \cos \theta)) \tan (\theta/2) = 2R ( \sin \theta) \tan (\theta/2) d \theta</math> | ||
| + | |||
| + | |||
| + | integrating | ||
| + | |||
| + | :<math>x=R(\theta - \sin(\theta)) + constant</math> | ||
| + | |||
| + | |||
| + | If<math> x=0</math> when <math>\theta =0</math> then the constant = 0 | ||
| + | |||
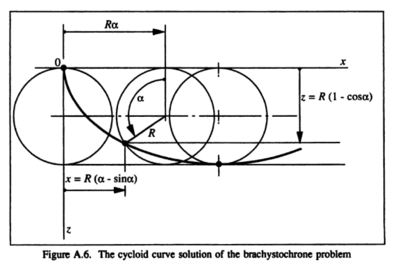
| + | The path of least time followed by the bead will be that traced out by the rim of a rolling circle (wheel) of radius R that rolls counter clockwise with complete slipping as is moves forward. | ||
| + | |||
| + | [[File:Forest_UCM_Brachystochrone_path.png | 400px]] | ||
| + | |||
| + | === Soap film (cycloid) === | ||
| + | |||
| + | consider the problem of the soap bubble formed between two circular rings. You stack two rings on top of each other in soapy water and then pull them apart after removing them from the water together where a film is created between the rings in a cylindrical shape. | ||
| + | |||
| + | what is the minimal area formed by the soap bubble | ||
| + | |||
| + | :<math>dA = 2 \pi y ds = 2 \pi y \sqrt{(dx)^2 + (dy)^2} = 2 \pi y \left ( 1 + (y^{\prime}(x))^2 \right )^{\frac{1}{2}} dx</math> | ||
| + | |||
| + | : <math>A = \int 2 \pi y \left ( 1 + (y^{\prime}(x))^2 \right )^{\frac{1}{2}}dx</math> | ||
| + | |||
| + | :<math> f(y(x),y^{\prime}(x);x) = y \left ( 1 + (y^{\prime}(x))^2 \right )^{\frac{1}{2}} </math> | ||
| + | |||
| + | ;Since the above function appears to be independent of x and | ||
| + | |||
| + | ::<math>\frac{\partial f }{\partial y} \ne 0</math> | ||
| + | |||
| + | the alternate form of Euler-Lagrange's equation (the first integral) is used | ||
| + | |||
| + | : <math> \frac{\partial f}{\partial x} - \frac{d }{dx} \left [f- y^{\prime}\frac{\partial f}{\partial y^{\prime}(x) }\right ] =0</math> | ||
| + | |||
| + | |||
| + | ::<math>\frac{\partial f }{\partial x} = 0 \Rightarrow \left [f- y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ] =</math>constant | ||
| + | |||
| + | :<math>\left [f- y^{\prime}\frac{\partial f}{\partial y^{\prime} }\right ] = y\left ( 1 + (y^{\prime})^2 \right )^{\frac{1}{2}} - \frac{yy^{\prime}(y^{\prime})}{\left ( 1 + (y^{\prime})^2 \right )^{\frac{1}{2}} }</math> | ||
| + | ::<math>= \frac{y\left ( 1 + (y^{\prime})^2 \right ) - y(y^{\prime})^2}{\left ( 1 + (y^{\prime})^2 \right )^{\frac{1}{2}} }= \frac{y}{\left ( 1 + (y^{\prime})^2 \right )^{\frac{1}{2}} }=</math> constant | ||
| + | |||
| + | or | ||
| + | |||
| + | |||
| + | :<math> \frac{y^2}{\left ( 1 + (y^{\prime})^2 \right ) }=C^2</math> | ||
| + | |||
| + | :<math>\Rightarrow y^{\prime} = \frac{dy}{dx} = \frac{\sqrt{y^2-C^2}}{C}</math> | ||
| + | |||
| + | as long as the smallest value of y is larger than the constant C | ||
| + | |||
| + | :<math>x = \int \frac{C}{\sqrt{y^2-C^2}} dy = C \cosh^{-1}(\frac{y}{C}) + K</math> | ||
| + | |||
| + | or | ||
| + | |||
| + | :<math> y = C \cosh(\frac{x-K}{C})</math> | ||
| + | C and K are constants used to position the area so it goes through the desired points in space | ||
https://www.fields.utoronto.ca/programs/scientific/12-13/Marsden/FieldsSS2-FinalSlidesJuly2012.pdf | https://www.fields.utoronto.ca/programs/scientific/12-13/Marsden/FieldsSS2-FinalSlidesJuly2012.pdf | ||
| + | |||
| + | http://books.google.com/books?id=4iABL2l_i98C&pg=PA323&lpg=PA323&dq=euler+lagrange+equation+alternate+form&source=bl&ots=sJfsaoONwO&sig=IiBUDYL4sOoQxMJ9tYcTHi4Agbw&hl=en&sa=X&ei=yNhDVMLKD8WGigLJroGABQ&ved=0CFoQ6AEwCQ#v=onepage&q=euler%20lagrange%20equation%20alternate%20form&f=false | ||
[[Forest_Ugrad_ClassicalMechanics]] | [[Forest_Ugrad_ClassicalMechanics]] | ||
Latest revision as of 12:31, 23 October 2014
Calculus of Variations
Fermat's Principle
Fermats principle is that light takes a path between two points that requires the least amount of time.
If we let S represent the path of light between two points then
light takes the time to travel between two points can be expressed as
The index of refraction is denoted as
for light traversing an interface with an nindex of refraction $n_1$ on one side and $n_2$ on the other side we would hav e
take derivative of time with respect to to find a minimum for the time of flight
or
Generalizing Fermat's principle to determining the shorest path
One can apply Fermat's principle to show that the shortest path between two points is a straight line.
In 2-D one can write the differential path length as
using chain rule
the the path length between two points and is
adding up the minimum of the integrand function is one way to minimize the integral ( or path length)
let
- Note
- in the above is the independent variable in the function while and depend on . The semicolon is used to separate them with the independent variable appearing last
the path integral can now be written in terms of dx such that
To consider deviation away from the function is introduced to denote deviations away from the shortest line and the parameter is introduced to weight that deviation
- = the difference between the current curve and the shortest path.
let
- = A path that is not the shortest path between two points.
- Note
- It is stipulated that is independent of to ensure that in the limit, and
- ie; both the function and its derivative approach
let
the deviations in the various paths can be expressed in terms of a differential of the above integral for the path length with respect to the parameter as this parameter changes the deviation
The second integral above can by evaluated using integration by parts as
let
- :
- the difference between the end points should be zero because to keep be sure that the endpoints are the same
The above integral is equivalent to
For the above to be true for any function then it follows that should be zero
- = Constant
integrating
http://scipp.ucsc.edu/~haber/ph5B/fermat09.pdf
Euler-Lagrange Equation
The Euler- Lagrange Equation is written as
the above becomes a condition for minimizing the "Action"
Shortest distance betwen two points revisited
Let's consider the problem of determining the shortest distance between two points again.
Previously we determined the shortest distance by assuming only two variables. One was the independent variable and the other, (), was dependent on .
What happens if the above assumption is relaxed.
To consider all possible paths between two point we should write the path in parameteric form
The functions above are assumed to be continuous and have continuous second derivatives.
- Note
- the above parameterization includes our previous assumption of the variables if we just let .
- Other examples
- parabola
- circle
- ellips
- hyperbola
The length of a small segment of the path is given by
now instead of
you have
and the path integral changes from
to
the same arguments are made again
instead of
You now have
instead of
you now have
If you require that the integral not deviate from the shortest path between two points (i.e. it is stationary)
Then you are requiring that the integral from path segments that deviate from the shortest path satisfies the equation
- and
when
- for any function and that vanish at the endpoints and
or
similarly
Apply Euler-Lagrange to shortest path problem revisited
- = constant
similarly
Shortest path along a sphere
- = constant
Assume the location of the first point is at </math>
The curves of constant are lines of longitude and are great circles which are geodesics (the shortest lines between two points on a shphere)
Brachystochrone problem
In the brachystochrone (Greek for "shortest time") problem we are determining the path of a bead between two points that takes the shortest time when the bead is constrained to slide along a wire without friction and in the presence of gravity.
The fall time for the bead is given by
Using conservation of energy one may cast the beads velocity as
This problem is similar to the shortest distance between two points problem above in that one can write the time variation that you wish to minimize in terms of the path variation
This time however there is an external driving force which is a function of the distance . So instead of writing the distance variation as a function of with we will want to write it as a function of with
then
since is an explicit function of and
then we can use the Euler-Lagrange equation
- Notice how the variables x & y have been interchanged now that is written as a function of whereas before was written as a function of
- constant
-
- = constant
or
- = constant
- using the foresight of working this problem before , the convenient constant is defined as
let
returning to the substitution used for integration we have
alternate form of Euler-Lagrange equation
Brachistochrone problem revisited
Consider the Brachistochrone problem again but this time do not cast as a function of
The fall time for the bead is given by
Using conservation of energy one may cast the beads velocity as
This problem is similar to the shortest distance between two points problem above in that one can write the time variation that you wish to minimize in terms of the path variation
then
- BUT the above function appears to be independent of x and
alternate form of Euler-Lagrange's equation (the first integral)
In the previous problems of finding the shortest distance between two point in 2-D and 2 point on the surface of the sphere, the extreme function was independent of (or )
for the 2-D line
for the geodesic
there are some problems where the functional dependence of on or is not explicit
because of this we need to use the chain to take the total derivative of the function with respect to
- Notice
-
substitution in for and moving terms around
rearranging
Euler-Lagrange Equation
Then the alternate form of Euler-Lagrange's equation is
returning to Brachistochrone
Returning back the the brachistochrone problem
- Since the above function appears to be independent of x and
the alternate form of Euler-Lagrange's equation (the first integral) is used
- constant
let
substituting
to find just return to definition of
integrating
If when then the constant = 0
The path of least time followed by the bead will be that traced out by the rim of a rolling circle (wheel) of radius R that rolls counter clockwise with complete slipping as is moves forward.
Soap film (cycloid)
consider the problem of the soap bubble formed between two circular rings. You stack two rings on top of each other in soapy water and then pull them apart after removing them from the water together where a film is created between the rings in a cylindrical shape.
what is the minimal area formed by the soap bubble
- Since the above function appears to be independent of x and
the alternate form of Euler-Lagrange's equation (the first integral) is used
- constant
-
- constant
or
as long as the smallest value of y is larger than the constant C
or
C and K are constants used to position the area so it goes through the desired points in space
https://www.fields.utoronto.ca/programs/scientific/12-13/Marsden/FieldsSS2-FinalSlidesJuly2012.pdf