Forest UCM CoV

Calculus of Variations

Fermat's Principle

Fermats principle is that light takes a path between two points that requires the least amount of time.

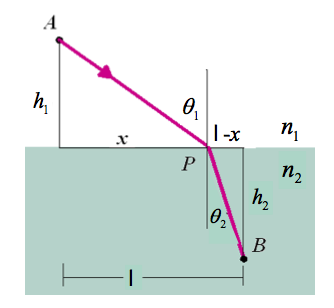
If we let S represent the path of light between two points then

[math]S=vt[/math]

light takes the time [math]t[/math] to travel between two points can be expressed as

[math]t = \int_A^B dt =\int_A^B \frac{1}{v} ds [/math]

The index of refraction is denoted as

[math]n=\frac{c}{v}[/math]

[math]t = \int_A^B \frac{n}{c} ds [/math]

for light traversing an interface with an nindex of refraction $n_1$ on one side and $n_2$ on the other side we would hav e

[math]t = \int_A^I \frac{n_1}{c} ds+ \int_I^B \frac{n_2}{c} ds [/math]

[math]= \frac{n_1}{c}\int_A^I ds+ \frac{n_2}{c} \int_I^B ds [/math]

[math]= \frac{n_1}{c}\sqrt{h_1^2 + x^2}+ \frac{n_2}{c} \sqrt{h_2^2 + (\ell -x)^2} [/math]

take derivative of time with respect to [math]x[/math] to find a minimum for the time of flight

[math] \frac{d t}{dx} = 0[/math]

[math] \Rightarrow 0 = \frac{d}{dx} \left ( \frac{n_1}{c}\left ( h_1^2 + x^2 \right )^{\frac{1}{2}}+ \frac{n_2}{c} \left (h_2^2 + (\ell -x)^2 \right)^{\frac{1}{2}} \right )[/math]

[math] = \frac{n_1}{c}\left( h_1^2 + x^2 \right )^{\frac{-1}{2}} (2x) + \frac{n_2}{c} \left (h_2^2 + (\ell -x)^2 \right)^{\frac{-1}{2}} 2(\ell -x)(-1)[/math]

[math] = \frac{n_1}{c}\frac{x}{\sqrt{ h_1^2 + x^2 }} + \frac{n_2}{c} \frac{(\ell -x)(-1)}{\sqrt{h_2^2 + (\ell -x)^2}} [/math]

[math] = n_1\frac{x}{\sqrt{ h_1^2 + x^2 }} - n_2 \frac{\ell -x}{\sqrt{h_2^2 + (\ell -x)^2}} [/math]

[math] \Rightarrow n_1\frac{x}{\sqrt{ h_1^2 + x^2 }} = n_2 \frac{\ell -x}{\sqrt{h_2^2 + (\ell -x)^2}} [/math]

or

[math] \Rightarrow n_1\sin(\theta_1) = n_2 \sin(\theta_2) [/math]

Generalizing Fermat's principle to determining the shorest path

One can apply Fermat's principle to show that the shortest path between two points is a straight line.

In 2-D one can write the differential path length as

[math]ds=\sqrt{dx^2+dy^2}[/math]

using chain rule

[math]dy = \frac{dy}{dx} dx \equiv y^{\prime}(x) dx[/math]

the the path length between two points [math](x_1,y_1)[/math] and [math](x_2,y_2)[/math] is

[math]S = \int_{(x_1,y_1)}^{(x_2,y_2)} ds= \int_{(x_1,y_1)}^{(x_2,y_2)} \sqrt{dx^2+dy^2}[/math]

[math] = \int_{(x_1,y_1)}^{(x_2,y_2)} \sqrt{dx^2+\left ( y^{\prime}(x) dx\right)^2}[/math]

[math] = \int_{(x_1,y_1)}^{(x_2,y_2)} \sqrt{1+y^{\prime}(x)^2}dx[/math]

adding up the minimum of the integrand function is one way to minimize the integral ( or path length)

let

[math]f(y,y^{\prime},x) \equiv \sqrt{1+y^{\prime}(x)^2}[/math]

the path integral can now be written in terms of dx such that

[math]S= \int_{(x_1)}^{(x_2)} f(y,y^{\prime},x) dx[/math]

To consider deviation away from [math]y(x)[/math] the function [math]\eta(x)[/math] is introduced to denote deviations away from the shortest line and the parameter [math]\alpha[/math] is introduced to weight that deviation

[math]\eta(x)[/math] = the difference between the current curve and the shortest path.

let

[math]Y(x) = y(x) + \alpha \eta(x)[/math] = A path that is not the shortest path between two points.

let

[math]S(\alpha)= \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx[/math]

[math]= \int_{(x_1)}^{(x_2)} f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) dx[/math]

the deviations in the various paths can be expressed in terms of a differentiate of the above integral with respect to the parameter [math]\alpha[/math] as this parameter changes the deviation

[math]\frac{\partial}{\partial \alpha} f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) = \frac{\partial y}{\partial \alpha}\frac{\partial f}{\partial y}+\frac{\partial y^{\prime}}{\partial \alpha} \frac{\partial f}{\partial y^{\prime}}= \eta \frac{\partial f}{\partial y}+\eta^{\prime} \frac{\partial f}{\partial y^{\prime}}[/math]

[math]\frac{dS(\alpha)}{d \alpha}=\frac{d}{d \alpha} \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx[/math]

[math]= \int_{(x_1)}^{(x_2)} \frac{d}{d \alpha}f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) dx[/math]

[math]= \int_{(x_1)}^{(x_2)} \left ( \eta \frac{\partial f}{\partial y}+\eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx[/math]

[math]= \int_{(x_1)}^{(x_2)} \left ( \eta \frac{\partial f}{\partial y} \right ) + \int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx[/math]

The second integral above can by evaluated using integration by parts as

let

[math]u = \frac{\partial f}{\partial y^{\prime}} \;\;\;\;\;\;\;\;\;\;\;\; dv = \eta^{\prime} dx[/math]

[math]du = \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \;\;\;\;\;\;\;\;\;\;\;\; v=\eta [/math]

[math]\int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx = \left [ \eta \frac{\partial f}{\partial y^{\prime}} \right ]_{x_1}^{x_2} - \int_{(x_1)}^{(x_2)} \eta \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right )dx [/math]

[math]\left [ \eta \frac{\partial f}{\partial y^{\prime}} \right ]_{x_1}^{x_2}[/math] : the difference between the end points should be zero because [math]\eta(x_1) = \eta(x_2)[/math] to keep be sure that the endpoints are the same

[math]\int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx = 0 - \int_{(x_1)}^{(x_2)} \eta \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right )dx [/math]

[math]\frac{dS(\alpha)}{d \alpha}=\frac{d}{d \alpha} \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx[/math]

[math]= \int_{(x_1)}^{(x_2)} \left ( \eta \frac{\partial f}{\partial y} \right ) - \int_{(x_1)}^{(x_2)} \eta \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right )dx [/math]

[math]= \int_{(x_1)}^{(x_2)} \eta \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] dx [/math]

The above integral is equivalent to

[math]\int \eta(x) g(x) = 0[/math]

For the above to be true for any function [math]\eta(x)[/math] then it follows that [math]g(x)[/math] should be zero

[math] \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] =0 [/math]

[math]f(y,y^{\prime},x) \equiv \sqrt{1+y^{\prime}(x)^2}[/math]

[math]\frac{\partial f}{\partial y} = \frac{\partial }{\partial y} \sqrt{1+y^{\prime}(x)^2} = 0 [/math]

[math] \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) = \frac{d}{dx} \left ( \frac{\partial ( \sqrt{1+y^{\prime}(x)^2})}{\partial y^{\prime}} \right ) = \frac{\partial f}{\partial y} = 0 [/math]

[math] \Rightarrow \left ( \frac{\partial ( \sqrt{1+y^{\prime}(x)^2})}{\partial y^{\prime}} \right ) [/math]= Constant

[math] \frac{y^{\prime}(x)}{ \sqrt{1+y^{\prime}(x)^2}} = C [/math]

[math] \left ( y^{\prime}(x)\right )^2=C^2 \left ( 1+y^{\prime}(x)^2\right ) [/math]

[math] \left (1 - C^2 \right ) \left ( y^{\prime(x) }\right )^2=C^2 [/math]

[math] \left ( y^{\prime}(x)\right )^2=\frac{C^2}{1 - C^2) } [/math]

[math] y^{\prime}(x)=\sqrt{\frac{C^2}{1 - C^2) } } \equiv m[/math]

integrating

[math]y =mx+b[/math]

http://scipp.ucsc.edu/~haber/ph5B/fermat09.pdf

Euler-Lagrange Equation

The Euler- Lagrange Equation is written as

[math] \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] =0 [/math]

the above becomes a condition for minimizing the "Action"

https://www.fields.utoronto.ca/programs/scientific/12-13/Marsden/FieldsSS2-FinalSlidesJuly2012.pdf

Forest_Ugrad_ClassicalMechanics