Difference between revisions of "Forest UCM NLM"
Jump to navigation
Jump to search
| Line 38: | Line 38: | ||
:<math>\vec{v}</math> = <math>\frac{d \vec{r}}{dt}</math> = <math>\frac{d x}{dt}\hat{i} + \frac{d y}{dt}\hat{i} + \frac{d z}{dt}\hat{i} </math> | :<math>\vec{v}</math> = <math>\frac{d \vec{r}}{dt}</math> = <math>\frac{d x}{dt}\hat{i} + \frac{d y}{dt}\hat{i} + \frac{d z}{dt}\hat{i} </math> | ||
| + | |||
| + | ===Polar=== | ||
| + | [[File:TF_UCM_PolarCoordSys.png| 200 px]] | ||
| + | |||
| + | |||
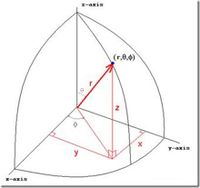
===Spherical=== | ===Spherical=== | ||
Revision as of 20:30, 17 June 2014
Newton's Laws of Motion
Limits of Classical Mechanic
Classical Mechanics is the formulations of physics developed by Newton (1642-1727), Lagrange(1736-1813), and Hamilton(1805-1865).
It may be used to describe the motion of objects which are not moving at high speeds (0.1) nor are microscopically small ( ).
The laws are formulated in terms of space, time, mass, and force:
Space and Time
Space
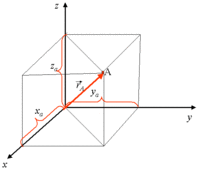
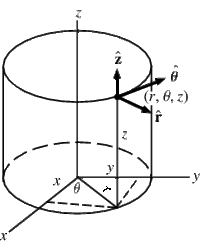
Cartesian, Spherical, and Cylindrical coordinate systems are commonly used to describe three-dimensional space.
Cartesian
Vector Notation convention:
Position:
Velocity:
- = =
cartesian unit vectors do not change with time (unit vectors for other coordinate system types do)
- = =
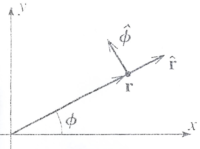
Polar