Difference between revisions of "Anisotropic n's vs. isotropic ones"
| (31 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [https://wiki.iac.isu.edu/index.php/ | + | [https://wiki.iac.isu.edu/index.php/Roman_calculation Go Back] |
| − | == | + | ==Motivation: there are a lot of source of isotropic neutrons=== |
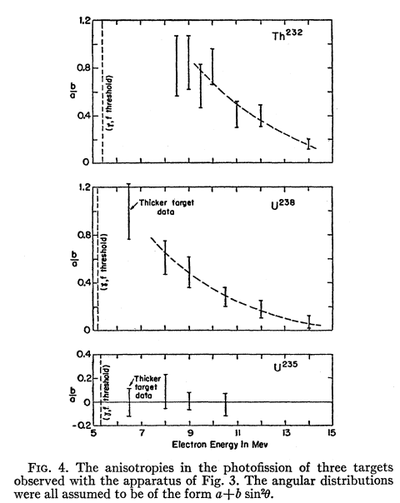
| − | + | 1. Winhold and Halpern, Phys.Rev. 103 4, 990 (1956). | |
| − | |||
| − | |||
| + | :The observation were consistent with the assumption that | ||
| + | :anisotropic fission is due solely to photons with-in about | ||
| + | :3 MeV of the fission threshold". | ||
| − | : | + | |
| − | : | + | :The photons in the giant resonance region were found |
| + | :to produce essentially isotropic fission | ||
[[File:Winhold fig.4.png | 400px]] | [[File:Winhold fig.4.png | 400px]] | ||
| + | |||
| + | |||
| + | 2. A lot of other papers. | ||
| + | |||
| + | 3. Isotropic neutrons from (<math>\gamma</math>,n) channel and (<math>\gamma</math>,2n) channel | ||
==Anisotropic n's vs. isotropic ones== | ==Anisotropic n's vs. isotropic ones== | ||
| − | Say, we have only anisotropic neutrons | + | Say, we have only anisotropic neutrons with 1.25 calculated ratio: |
| + | |||
| + | :<math>N(90^o) = 125</math> | ||
| + | :<math>N(0^o) = 100</math> | ||
| + | |||
| + | The calculated asymmetry would be: | ||
| − | :<math>\ | + | :<math>A = \frac{N(90) - N(0)}{N(90) + N(0)} = \frac{25}{225} = 11.1%</math> |
| − | |||
| − | |||
| − | |||
| + | Now, say, we have extra 100 isotropic neutrons for each detector: | ||
| + | :<math>N(90^o) = 100</math> | ||
| + | :<math>N(0^o) = 100</math> | ||
| − | + | The total number of neutrons become: | |
| − | :<math> | + | :<math>N(90^o) = 100 +125 = 225</math> |
| − | :<math> | + | :<math>N(0^o) = 100 + 100 = 200</math> |
So the calculated asymmetry would be: | So the calculated asymmetry would be: | ||
| − | :<math>A = \frac{ | + | :<math>A = \frac{N(90) - N(0)}{N(90) + N(0)} = \frac{25}{425} = 5.9%</math> |
| − | + | So if we would have about the same number of isotropic and anisotropic neutrons that would be reduced the expectation values of asymmetry almost in two times!!!. | |
| + | |||
| + | |||
| + | '''We need to count isotropic and anisotropic neutrons to estimate the effect of washing out the anisotropy by isotropic neutrons.''' | ||
| Line 49: | Line 64: | ||
Source of isotropic neutrons: | Source of isotropic neutrons: | ||
*(<math>\gamma</math>,f) channel due to photons out of 3 MeV of the fission threshold | *(<math>\gamma</math>,f) channel due to photons out of 3 MeV of the fission threshold | ||
| − | *(<math>\gamma</math>,n) channel | + | *(<math>\gamma</math>,n) channel. |
| − | *(<math>\gamma</math>,2n) channel | + | *(<math>\gamma</math>,2n) channel. |
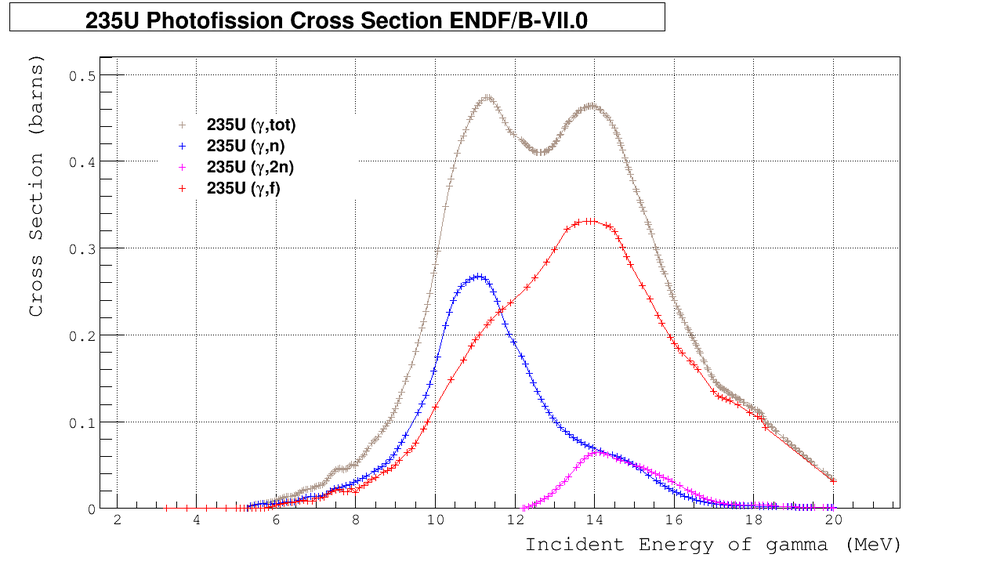
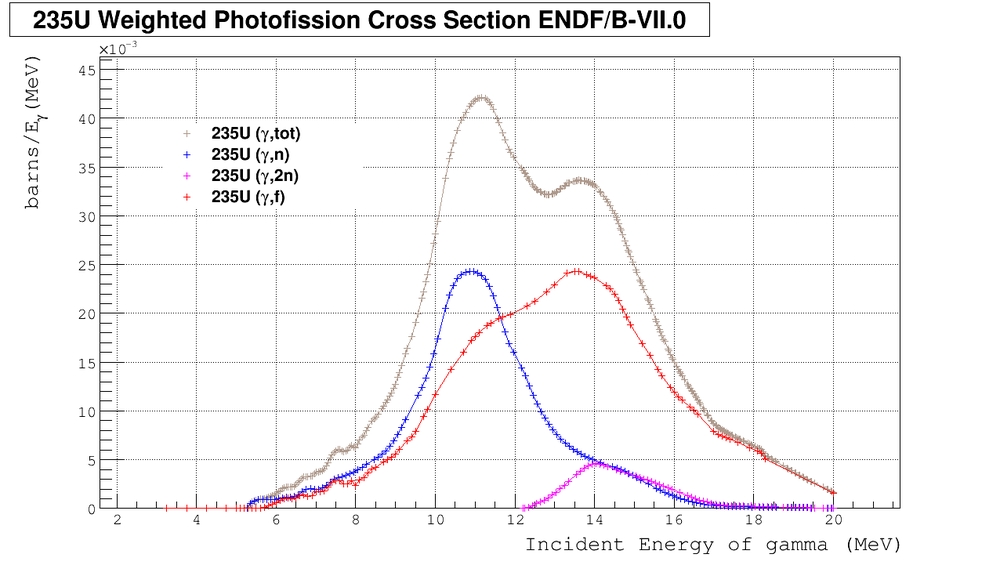
==U Photo-fission Cross Section== | ==U Photo-fission Cross Section== | ||
| − | |||
| − | [[File: | + | [[File:U235.sigma.01.png | 1000px]] |
| + | |||
| + | [[File:U235.sigmaflux.01.png | 1000px]] | ||
| + | |||
| + | From the plot above we can expect significant number of isotropic neutrons from (<math>\gamma</math>,n) and (<math>\gamma</math>,2n) channels. So the effect of washing out the anisotropy by isotropic neutrons should be significant and should be estimated. | ||
| + | |||
| + | ==Let's count isotropic and anisotropic neutrons== | ||
| + | |||
| + | Assuming conservatively: | ||
| + | |||
| + | |||
| + | Source of anisotropic neutrons: | ||
| + | *(<math>\gamma</math>,f) channel for all incident gammas. In reality the number of anisotropic neutrons will reduce with increasing the energy of gammas. | ||
| + | |||
| + | Source of isotropic neutrons: | ||
| + | *(<math>\gamma</math>,n) channel | ||
| + | *(<math>\gamma</math>,2n) channel | ||
| + | |||
| + | |||
| + | We can calculate the relative number of neutrons from different channels using formulas: | ||
| + | |||
| + | :<math>N_n = \frac{\int \sigma_n \Phi(E_{\gamma}) dE_{\gamma}}{\int \sigma_{tot} \Phi(E_{\gamma}) dE_{\gamma}}</math> | ||
| + | |||
| + | :<math>N_{2n} = \frac{\int \sigma_{2n} \Phi(E_{\gamma}) dE_{\gamma}}{\int \sigma_{tot} \Phi(E_{\gamma}) dE_{\gamma}}</math> | ||
| + | |||
| + | :<math>N_f = \frac{\int \sigma_f \Phi(E_{\gamma}) dE_{\gamma}}{\int \sigma_{tot} \Phi(E_{\gamma}) dE_{\gamma}}</math> | ||
| + | |||
| + | |||
| + | Using root simple integration procedure I found: | ||
| + | |||
| + | [[File:Table isotropic vs anisotropic event yields.png | 300px]] | ||
| + | |||
| + | |||
| + | |||
| + | So we have: | ||
| + | |||
| + | *total isotropic events yield from (<math>\gamma</math>,n) channel is about 35 % | ||
| + | *total isotropic events yield from (<math>\gamma</math>,2n) channel is about 5 % | ||
| + | *total anisotropic events yield from (<math>\gamma</math>,f) channel is about 60 % | ||
| + | |||
| + | |||
| + | Say we have total 100 events. Because we have 1n from (<math>\gamma</math>,n) channel, 2n neutron (<math>\gamma</math>,2n) channel and assuming we have 2n from (<math>\gamma</math>,f) channel: | ||
| + | |||
| + | *total number of isotropic neutrons from (<math>\gamma</math>,n) channel: 35 n's | ||
| + | *total number of isotropic neutrons from (<math>\gamma</math>,2n) channel: 10 n's | ||
| + | *total number of anisotropic neutrons from (<math>\gamma</math>,f) channel: 120 n's | ||
| + | |||
| + | |||
| + | So we have: | ||
| + | |||
| + | *total isotropic neutrons yields is about (35+10)/(35+10+120) = 27 % | ||
| + | *total anisotropic neutrons yields is about (120)/(35+10+120) = 73 % | ||
| + | |||
| + | |||
| + | The yields above are for 4<math>\pi</math> geometry. Now we need to calculate how many isotropic and anisotropic neutrons comes to detectors. Because anisotropic neutrons mostly comes at <math>\Theta = 90^o</math> the relative number of anisotropic neutrons at detectors will increase (will be more than 73 %). | ||
Latest revision as of 19:04, 24 May 2012
Motivation: there are a lot of source of isotropic neutrons=
1. Winhold and Halpern, Phys.Rev. 103 4, 990 (1956).
- The observation were consistent with the assumption that
- anisotropic fission is due solely to photons with-in about
- 3 MeV of the fission threshold".
- The photons in the giant resonance region were found
- to produce essentially isotropic fission
2. A lot of other papers.
3. Isotropic neutrons from (,n) channel and (,2n) channel
Anisotropic n's vs. isotropic ones
Say, we have only anisotropic neutrons with 1.25 calculated ratio:
The calculated asymmetry would be:
Now, say, we have extra 100 isotropic neutrons for each detector:
The total number of neutrons become:
So the calculated asymmetry would be:
So if we would have about the same number of isotropic and anisotropic neutrons that would be reduced the expectation values of asymmetry almost in two times!!!.
We need to count isotropic and anisotropic neutrons to estimate the effect of washing out the anisotropy by isotropic neutrons.
Source of anisotropic neutrons:
- (,f) channel due to photons with-in about 3 MeV of the fission threshold
Source of isotropic neutrons:
- (,f) channel due to photons out of 3 MeV of the fission threshold
- (,n) channel.
- (,2n) channel.
U Photo-fission Cross Section
From the plot above we can expect significant number of isotropic neutrons from (,n) and (,2n) channels. So the effect of washing out the anisotropy by isotropic neutrons should be significant and should be estimated.
Let's count isotropic and anisotropic neutrons
Assuming conservatively:
Source of anisotropic neutrons:
- (,f) channel for all incident gammas. In reality the number of anisotropic neutrons will reduce with increasing the energy of gammas.
Source of isotropic neutrons:
- (,n) channel
- (,2n) channel
We can calculate the relative number of neutrons from different channels using formulas:
Using root simple integration procedure I found:
So we have:
- total isotropic events yield from (,n) channel is about 35 %
- total isotropic events yield from (,2n) channel is about 5 %
- total anisotropic events yield from (,f) channel is about 60 %
Say we have total 100 events. Because we have 1n from (,n) channel, 2n neutron (,2n) channel and assuming we have 2n from (,f) channel:
- total number of isotropic neutrons from (,n) channel: 35 n's
- total number of isotropic neutrons from (,2n) channel: 10 n's
- total number of anisotropic neutrons from (,f) channel: 120 n's
So we have:
- total isotropic neutrons yields is about (35+10)/(35+10+120) = 27 %
- total anisotropic neutrons yields is about (120)/(35+10+120) = 73 %
The yields above are for 4 geometry. Now we need to calculate how many isotropic and anisotropic neutrons comes to detectors. Because anisotropic neutrons mostly comes at the relative number of anisotropic neutrons at detectors will increase (will be more than 73 %).