Difference between revisions of "Pair Production Rate Calculation"
| (17 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | [https://wiki.iac.isu.edu/index.php/Roman_calculation Go Back] |
==LINAC parameters used in calculations== | ==LINAC parameters used in calculations== | ||
| Line 30: | Line 30: | ||
===1/2 mil of Al=== | ===1/2 mil of Al=== | ||
| − | #<math>\sigma_{brems}= | + | #<math>\sigma_{brems}=0.1\ \mbox{photons/electrons/MeV/r.l}</math> |
#<math>\mbox{r.l.(Al)} = 8.89\ \mbox{cm}</math> | #<math>\mbox{r.l.(Al)} = 8.89\ \mbox{cm}</math> | ||
#<math>\mbox{radiator}\ \mbox{thickness} = 12.5\ \mu m</math> | #<math>\mbox{radiator}\ \mbox{thickness} = 12.5\ \mu m</math> | ||
| Line 37: | Line 37: | ||
<math>\frac{12.5\ \mu m}{8.89\ cm} = 1.41 \cdot 10^{-4}\ r.l.</math><br> | <math>\frac{12.5\ \mu m}{8.89\ cm} = 1.41 \cdot 10^{-4}\ r.l.</math><br> | ||
| − | <math>0.47 \cdot 10^{13}\ \frac{e^-}{sec} \times | + | <math>0.47 \cdot 10^{13}\ \frac{e^-}{sec} \times 0.1\ \frac{\gamma 's}{(e^- \cdot MeV \cdot r.l.)} \times 1.41 \cdot 10^{-4}\ r.l. \times 10\ MeV =0.66 \cdot 10^{9} \frac{\gamma}{sec}</math><br><br> |
'''Alex factor is 6.85 %''' | '''Alex factor is 6.85 %''' | ||
| − | <math> | + | <math>0.66 \cdot 10^{9} \frac{\gamma}{sec} \cdot 6.85\ % = 0.45 \cdot 10^{8} \frac{\gamma}{sec}</math><br><br> |
===Conversion factor from Ti to Al=== | ===Conversion factor from Ti to Al=== | ||
| Line 47: | Line 47: | ||
All my following calculation for pair production rate are based on (1/2) mil of Ti radiator. If we want to recalculate for (1/2) mil of Al converter we need to use the conversion factor: | All my following calculation for pair production rate are based on (1/2) mil of Ti radiator. If we want to recalculate for (1/2) mil of Al converter we need to use the conversion factor: | ||
| − | <math>\frac{ | + | <math>\frac{0.45\ (1/2\ mil\ of\ Al)}{1.12\ (1/2\ mil\ of\ Ti)} = 0.40 </math> |
===Appendix=== | ===Appendix=== | ||
| − | + | [[File:bremss44MeV.png | 500 px]] | |
| − | + | [[File:Al 44MeV.png | 500 px]] | |
| − | [[File:bremss44MeV.png | | ||
| − | |||
| − | |||
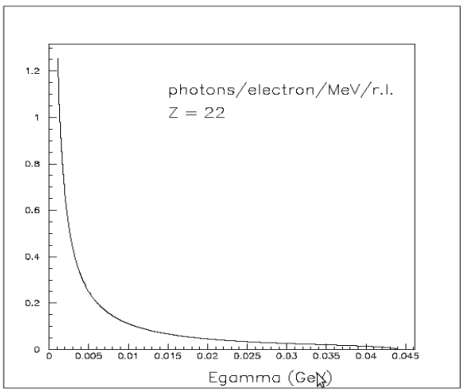
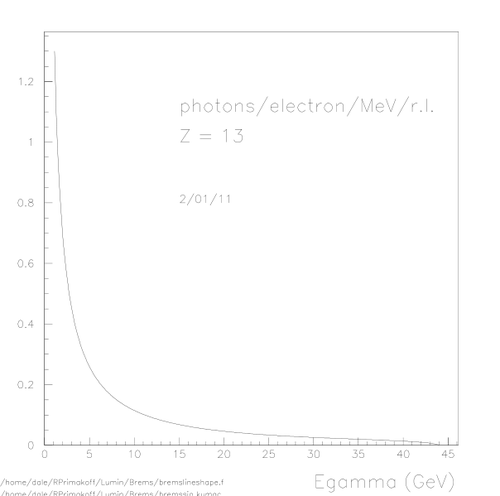
| − | + | in (10,20) MeV region we have about '''0.1 photons/electrons/MeV/r.l''' both for Ti and Al radiators | |
| − | |||
| − | |||
| − | |||
| − | in (10,20) MeV region we have about '''0.1 photons/electrons/MeV/r.l''' | ||
==Pair production rate== | ==Pair production rate== | ||
| Line 86: | Line 79: | ||
<math>\frac {1.12 \cdot 10^{8}\ \frac{\gamma}{sec} \times \sigma_{\mbox{pairs}} \times N_{\mbox{Nitrogen}}} {f} = 300\ \frac{\mbox{pairs}}{\mbox{pulse}} </math> | <math>\frac {1.12 \cdot 10^{8}\ \frac{\gamma}{sec} \times \sigma_{\mbox{pairs}} \times N_{\mbox{Nitrogen}}} {f} = 300\ \frac{\mbox{pairs}}{\mbox{pulse}} </math> | ||
| + | |||
| + | ===1 m of air vs. 3.0 um of Al converter=== | ||
| + | |||
| + | <math>\frac{300\ \frac{\mbox{pairs}}{\mbox{pulse}}} {3.38\ \frac{\mbox{pairs}}{\mbox{pulse}}} = 88.8\ \mbox{times!}</math> | ||
===Appendix=== | ===Appendix=== | ||
Latest revision as of 19:04, 24 May 2012
LINAC parameters used in calculations
1) pulse width 50 ps
2) pulse current 50 A
3) repetition rate 300 Hz
4) energy 44 MeV
Number of electrons/sec on radiator
Number of photons/sec out of radiator
1/2 mil of Ti
Alex factor is 6.85 %
1/2 mil of Al
Alex factor is 6.85 %
Conversion factor from Ti to Al
All my following calculation for pair production rate are based on (1/2) mil of Ti radiator. If we want to recalculate for (1/2) mil of Al converter we need to use the conversion factor:
Appendix
in (10,20) MeV region we have about 0.1 photons/electrons/MeV/r.l both for Ti and Al radiators
Pair production rate
out of Al converter
(by varying width we can vary the yield)
through 1 m of air
Assume air consists entirely from Nitrogen:
1 m of air vs. 3.0 um of Al converter
Appendix
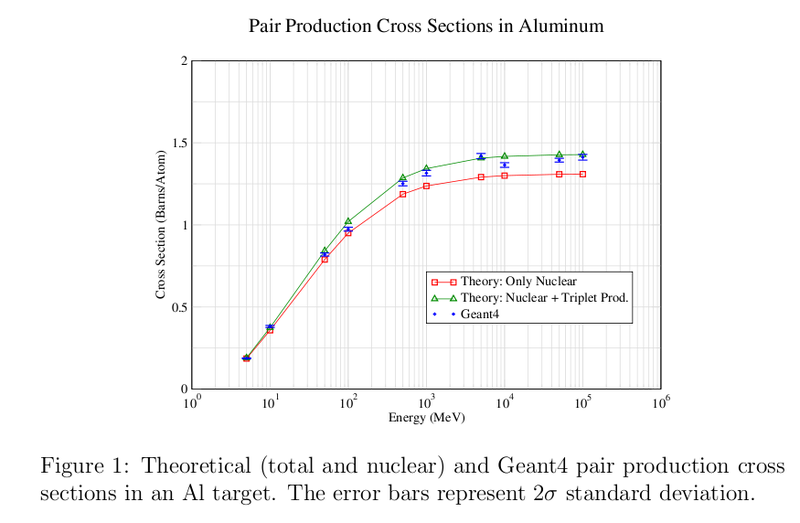
pair production cross sections in an Al target
Ref. Geant4 and Theoretical Pair Production Cross Sections for 1 MeV - 100 GeV photons in Aluminum. Vakho Makarashvili, December 18, 2007
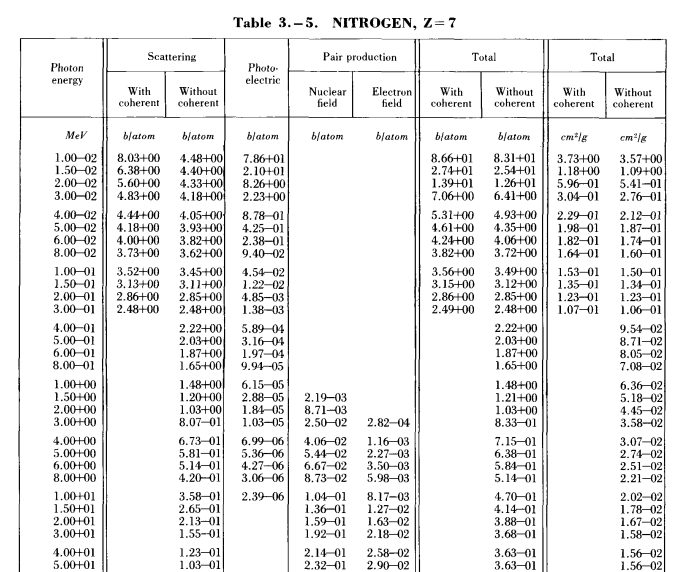
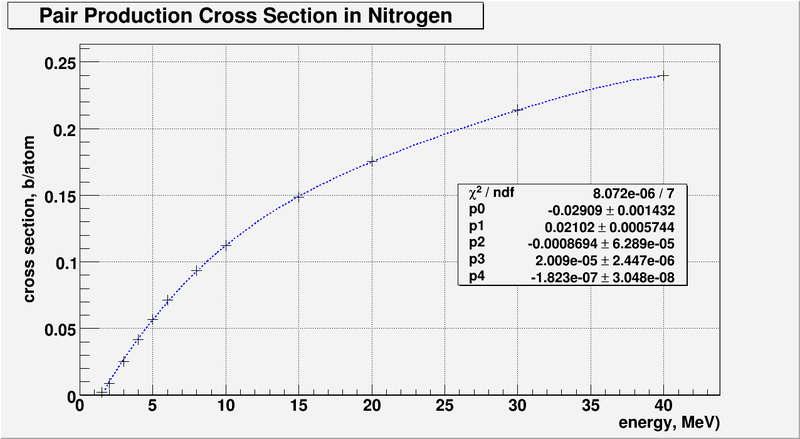
pair production cross sections in a Nitrogen
Ref. Photon Cross Section, Attenuation Coefficients, and Energy Absorption Coefficients From 10 keV to 100 Gev. J.H.Hubbell. Center for Radiation Research.National Bureau of Standards. Washington, D.C. 20234
Here I just plotted the table above for pair production cross section in (0, 40) MeV energy region