Difference between revisions of "Reading"
| Line 6: | Line 6: | ||
[http://www.scholarpedia.org/article/Nucleon_Form_factors#History] | [http://www.scholarpedia.org/article/Nucleon_Form_factors#History] | ||
| + | |||
| + | |||
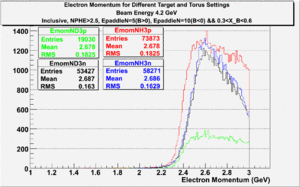
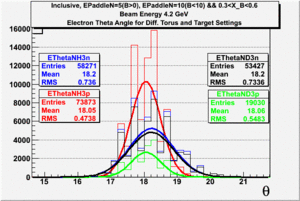
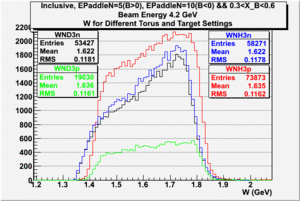
| + | The electron efficiency of individual scintillator detectors using the 4.2 GeV data for ND3 and NH3 targets is described below. In the final state, only electron detection was required(inclusive case). The contamination in the electron sample was removed by applying cuts described in the first chapter. The electron paddle number 10 (B<0) and 5 (B>0) were chosen respectively because they contained the most electron events in a first pass semi-inclusive pion analysis of the data set. The electron kinematics(Momentum, scattering angle and invariant mass) for these scintillators is shown on Fig. 3.1. | ||
| + | |||
| + | {| border="1" |cellpadding="20" cellspacing="0 | ||
| + | |- | ||
| + | |[[File:EmomInclusiveoverlay4-2GeV.gif|300px]] ||[[File:EthetaInclusiveoverlay4-2GeV.gif|300px]] || [[File:WInclusiveoverlay4-2GeV.gif|300px]] | ||
| + | |- | ||
| + | | Electron Momentum((NH3,B>0), (NH3,B<0), (ND3,B>0) && (ND3,B<0))|| Electron Scattering Angle <math>\theta</math>((NH3,B>0), (NH3,B<0), (ND3,B>0) && (ND3,B<0))|| W Invariant mass((NH3,B>0), (NH3,B<0), (ND3,B>0) && (ND3,B<0)) | ||
| + | |} | ||
| + | |||
| + | '''Figure 3.1. Electron Kinematics.''' | ||
| + | |||
| + | |||
| + | The goal of this thesis is to measure the semi-inclusive asymmetry when an electron and one pion are detected in the final state. This asymmetry may be written in terms of ratios of charged pion production cross sections from proton and neutron targets sorted according to the orientation of the incident electron helicity with respect to the target's polarization. Pions of opposite charge will be observed using the same scintillator by flipping the CLAS Torus magnetic field direction. Although the pions will be detected by the same detector elements, the electrons will intersect different detector elements. As a result, the electron efficiency will need to be evaluated in terms of the electron rate observed in two different scintillators detecting the same electron kinematics. The two scintillators are defined according to the polarity of the CLAS torus. | ||
| + | |||
| + | |||
| + | The ratio of the number of electrons weighted by the faraday cup for two different cases are following: | ||
| + | |||
| + | <math>\frac{ND3,B>0, E_{PaddleNumber}=5}{NH3,B<0,E_{PaddleNumber}=10}=1.55 \pm 0.15</math> | ||
| + | |||
| + | <math>\frac{ND3,B<0,E_{PaddleNumber}=10}{NH3,B>0,E_{PaddleNumber}=5}=0.55 \pm 0.06</math> | ||
| + | |||
| + | The ratios were taken for different types of target, so that we could compare the results to MAID 2007 Model. In order to make detector efficiency the same for two different cases (ND3,B>0 && NH3,B<0) and (ND3,B<0 && NH3,B>0), the ratios have been adjusted so that it equals to one. Each of the two cases are multiplied by so called, "correction coefficient". The coefficient for the case <math>\frac{ND3,B>0,E_{PaddleNumber}=5}{NH3,B<0,E_{PaddleNumber}=10}</math> is <math>0.645</math> and for the <math>\frac{ND3,B<0,E_{PaddleNumber}=10}{NH3,B>0,E_{PaddleNumber}=5}</math> it is <math>1.82</math>. | ||
| + | |||
| + | |||
| + | |||
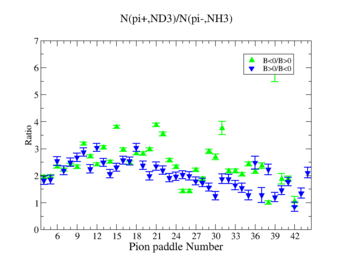
| + | In this chapter we discuss the pion efficiency in semi-inclusive case. The ratio of the pions detected in the scintillator paddles, located between the Cherenkov counter and electromagnetic calorimeter, is shown on Fig. 4.1. The ratios were taken for four different cases. Assuming that, for the inbending case positive pions and for the outbending case have the same trajectories(the same kinematics) and vice versa((the inbending,negative pion) and (the outbending, positive pions)).<br> | ||
| + | |||
| + | [[File:paddenumbvsratio.jpg|500px]]<br> | ||
| + | '''Figure 4.1. Pion paddle number vs Ratio.''' | ||
| + | |||
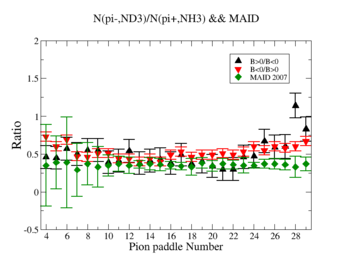
| + | We used MAID 2007 model to compare our results. Total cross section was calculated for the following invariant mass and four momentum transferred square: <math>1.7< W<1.8</math> and <math>Q^2=1.1 GeV^2</math>. <ref name="MAID2007" > http://wwwkph.kph.uni-mainz.de/MAID//maid2007/maid2007.html</ref>. After applying correction coefficients from inclusive cases, the ratios have been compared to the results from MAID2007. | ||
| + | |||
| + | ::<math>\sigma = \sigma_{T} + \epsilon \sigma_{L} + \sqrt{2\epsilon(1 + \epsilon)}\sigma_{LT} cos{\phi_{\pi}}^{CM} + \epsilon \sigma{TT} cos2{\phi_{\pi}}^{CM} + h \sqrt{2\epsilon (1-\epsilon)}\sigma_{LT^{\prime}}sin{\phi_{\pi}}^{CM} </math> | ||
| + | |||
| + | After applying correction coefficients from inclusive cases, the ratios have been compared to the results from MAID2007. | ||
| + | |||
| + | [[File:black_red_maid_inclusiveerror.png|350px]] [[File:green_blue_inclusiveerror.png|350px]] | ||
| + | |||
| + | '''Figure 4.2. Pion paddle number vs Ratio after correction.''' | ||
| + | |||
| + | Applied corrections are following: | ||
| + | |||
| + | <math>\frac{N(\pi^+,ND_3,B<0)}{N(\pi^-,NH_3,B>0)} \times 1.82</math> | ||
| + | |||
| + | <math>\frac{N(\pi^+,ND_3,B>0)}{N(\pi^-,NH_3,B<0)} \times 0.645</math> | ||
| + | |||
| + | <math>\frac{N(\pi^-,ND_3,B>0)}{N(\pi^+,NH_3,B<0)} \times 0.645</math> | ||
| + | |||
| + | <math>\frac{N(\pi^-,ND_3,B<0)}{N(\pi^+,NH_3,B>0)} \times 1.82</math> | ||
[http://wiki.iac.isu.edu/index.php/Delta_D_over_D Go Back] | [http://wiki.iac.isu.edu/index.php/Delta_D_over_D Go Back] | ||
Latest revision as of 23:34, 12 July 2011
Current quark
Radiative corrections
The electron efficiency of individual scintillator detectors using the 4.2 GeV data for ND3 and NH3 targets is described below. In the final state, only electron detection was required(inclusive case). The contamination in the electron sample was removed by applying cuts described in the first chapter. The electron paddle number 10 (B<0) and 5 (B>0) were chosen respectively because they contained the most electron events in a first pass semi-inclusive pion analysis of the data set. The electron kinematics(Momentum, scattering angle and invariant mass) for these scintillators is shown on Fig. 3.1.
 |
 |
|
| Electron Momentum((NH3,B>0), (NH3,B<0), (ND3,B>0) && (ND3,B<0)) | Electron Scattering Angle ((NH3,B>0), (NH3,B<0), (ND3,B>0) && (ND3,B<0)) | W Invariant mass((NH3,B>0), (NH3,B<0), (ND3,B>0) && (ND3,B<0)) |
Figure 3.1. Electron Kinematics.
The goal of this thesis is to measure the semi-inclusive asymmetry when an electron and one pion are detected in the final state. This asymmetry may be written in terms of ratios of charged pion production cross sections from proton and neutron targets sorted according to the orientation of the incident electron helicity with respect to the target's polarization. Pions of opposite charge will be observed using the same scintillator by flipping the CLAS Torus magnetic field direction. Although the pions will be detected by the same detector elements, the electrons will intersect different detector elements. As a result, the electron efficiency will need to be evaluated in terms of the electron rate observed in two different scintillators detecting the same electron kinematics. The two scintillators are defined according to the polarity of the CLAS torus.
The ratio of the number of electrons weighted by the faraday cup for two different cases are following:
The ratios were taken for different types of target, so that we could compare the results to MAID 2007 Model. In order to make detector efficiency the same for two different cases (ND3,B>0 && NH3,B<0) and (ND3,B<0 && NH3,B>0), the ratios have been adjusted so that it equals to one. Each of the two cases are multiplied by so called, "correction coefficient". The coefficient for the case is and for the it is .
In this chapter we discuss the pion efficiency in semi-inclusive case. The ratio of the pions detected in the scintillator paddles, located between the Cherenkov counter and electromagnetic calorimeter, is shown on Fig. 4.1. The ratios were taken for four different cases. Assuming that, for the inbending case positive pions and for the outbending case have the same trajectories(the same kinematics) and vice versa((the inbending,negative pion) and (the outbending, positive pions)).
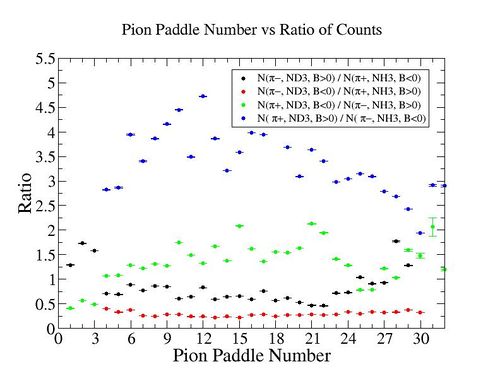
Figure 4.1. Pion paddle number vs Ratio.
We used MAID 2007 model to compare our results. Total cross section was calculated for the following invariant mass and four momentum transferred square: and . <ref name="MAID2007" > http://wwwkph.kph.uni-mainz.de/MAID//maid2007/maid2007.html</ref>. After applying correction coefficients from inclusive cases, the ratios have been compared to the results from MAID2007.
After applying correction coefficients from inclusive cases, the ratios have been compared to the results from MAID2007.
Figure 4.2. Pion paddle number vs Ratio after correction.
Applied corrections are following: