Anisotropic n's vs. isotropic ones

go back

Motivation: there are a lot of source of isotropic neutrons=

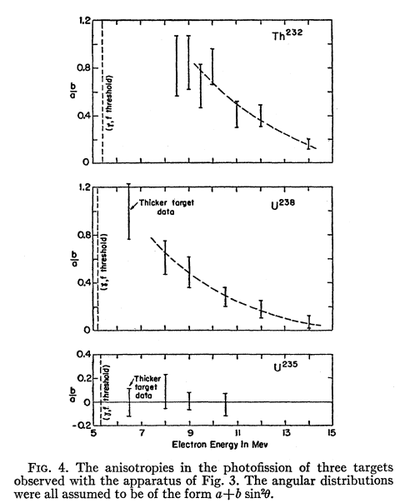
1. Winhold and Halpern, Phys.Rev. 103 4, 990 (1956).

The observation were consistent with the assumption that

anisotropic fission is due solely to photons with-in about

3 MeV of the fission threshold".

The photons in the giant resonance region were found

to produce essentially isotropic fission

2. A lot of other papers.

3. Isotropic neutrons from ([math]\gamma[/math],n) channel and ([math]\gamma[/math],2n) channel

Anisotropic n's vs. isotropic ones

Say, we have only anisotropic neutrons with 1.25 calculated ratio:

[math]N(90^o) = 125[/math]

[math]N(0^o) = 100[/math]

The calculated asymmetry would be:

[math]A = \frac{N(90) - N(0)}{N(90) + N(0)} = \frac{25}{225} = 11.1%[/math]

Now, say, we have extra 100 isotropic neutrons for each detector:

[math]N(90^o) = 100[/math]

[math]N(0^o) = 100[/math]

The total number of neutrons become:

[math]N(90^o) = 100 +125 = 225[/math]

[math]N(0^o) = 100 + 100 = 200[/math]

So the calculated asymmetry would be:

[math]A = \frac{N(90) - N(0)}{N(90) + N(0)} = \frac{25}{425} = 5.9%[/math]

So if we would have about the same number of isotropic and anisotropic neutrons that would be reduced the expectation values of asymmetry almost in two times!!!.

We need to count isotropic and anisotropic neutrons to estimate the effect of washing out the anisotropy by isotropic neutrons.

Source of anisotropic neutrons:

• ([math]\gamma[/math],f) channel due to photons with-in about 3 MeV of the fission threshold

Source of isotropic neutrons:

• ([math]\gamma[/math],f) channel due to photons out of 3 MeV of the fission threshold
• ([math]\gamma[/math],n) channel.
• ([math]\gamma[/math],2n) channel.

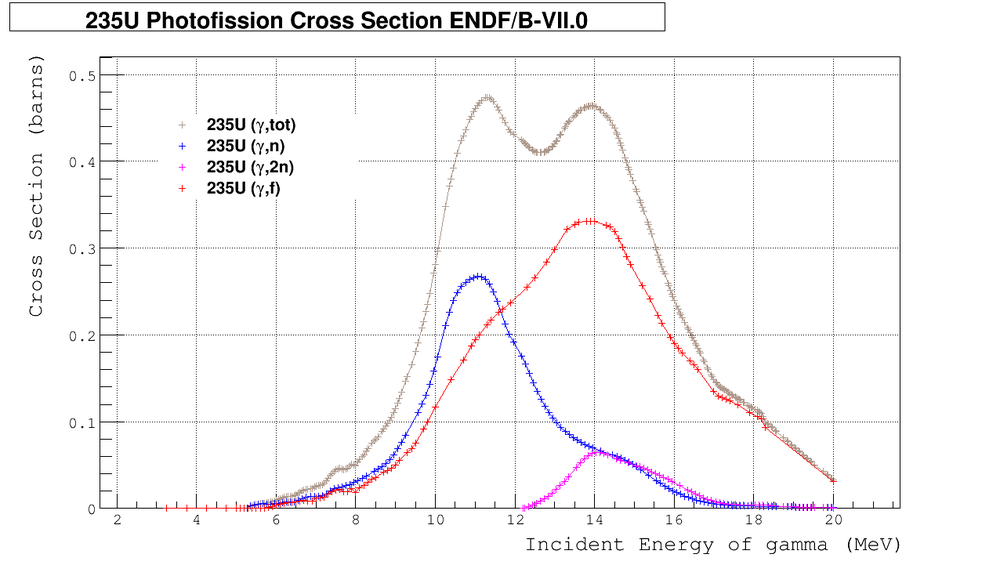
U Photo-fission Cross Section

Let's count isotropic and anisotropic neutrons

Assume most conservative:

Source of anisotropic neutrons:

• ([math]\gamma[/math],f) channel for all incident gammas. In reality the number of anisotropic neutrons will reduce with increasing the energy of gammas.

Source of isotropic neutrons:

• ([math]\gamma[/math],n) channel
• ([math]\gamma[/math],2n) channel

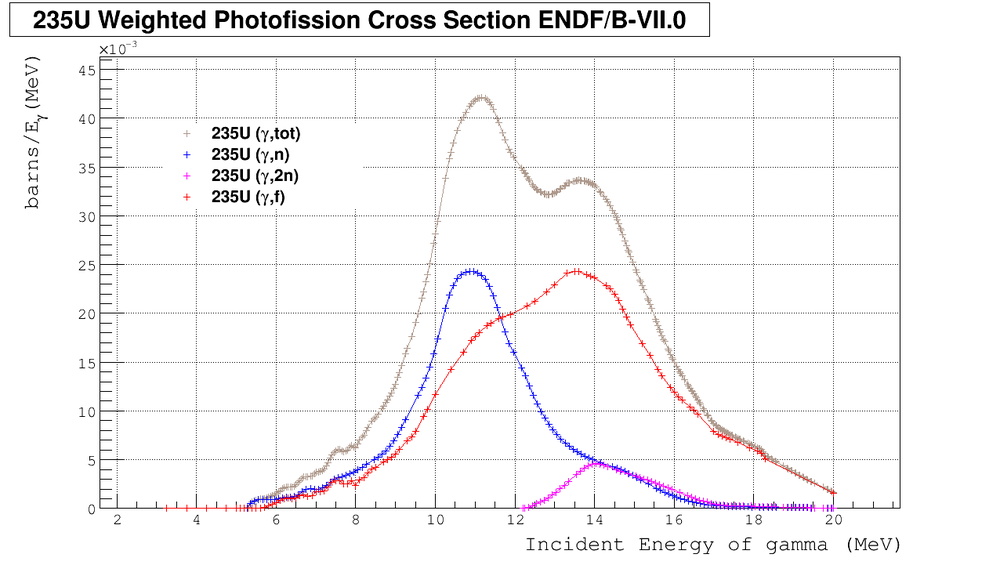
We can calculate the relative number of neutrons from different channels using formulas:

[math]N_f = \frac{\int \sigma_f \Phi(E_{\gamma}) dE_{\gamma}}{\int \sigma_{tot} \Phi(E_{\gamma}) dE_{\gamma}}[/math]

[math]N_n = \frac{\int \sigma_n \Phi(E_{\gamma}) dE_{\gamma}}{\int \sigma_{tot} \Phi(E_{\gamma}) dE_{\gamma}}[/math]

[math]N_{2n} = \frac{\int \sigma_{2n} \Phi(E_{\gamma}) dE_{\gamma}}{\int \sigma_{tot} \Phi(E_{\gamma}) dE_{\gamma}}[/math]

Using root to approximate sigma's by appropriate polynomials and using Maple to estimate integrals I found:

[math]N_f = a1\ %[/math]

[math]N_n = a2\ %[/math]

[math]N_{2n} = a3\ %[/math]