Difference between revisions of "Anisotropic n's vs. isotropic ones"
Jump to navigation
Jump to search
| Line 25: | Line 25: | ||
==Anisotropic n's vs. isotropic ones== | ==Anisotropic n's vs. isotropic ones== | ||
| − | Say, we have only anisotropic neutrons | + | Say, we have only anisotropic neutrons with 1.25 calculated ratio: |
| − | :<math> | + | :<math>N(90^o) = 125</math> |
| − | :<math>\ | + | :<math>N(0^o) = 100</math> |
| + | |||
| + | The calculated asymmetry would be: | ||
| + | |||
| + | :<math>A = \frac{N(90) - N(0)}{N(90) + N(0)} = \frac{25}{225} = 11.1%</math> | ||
| − | |||
| − | |||
| + | Now, say, we have extra 100 isotropic neutrons for each detector: | ||
| + | :<math>N(90^o) = 100</math> | ||
| + | :<math>N(0^o) = 100</math> | ||
| − | + | The total number of neutrons become: | |
| − | :<math> | + | :<math>N(90^o) = 100 +125 = 225</math> |
| − | :<math> | + | :<math>N(0^o) = 100 + 100 = 200</math> |
So the calculated asymmetry would be: | So the calculated asymmetry would be: | ||
| − | :<math>A = \frac{ | + | :<math>A = \frac{N(90) - N(0)}{N(90) + N(0)} = \frac{25}{425} = 5.9%</math> |
| + | |||
| + | :So if we would have about the same number of isotropic and anisotropic neutrons that would be reduced the expectation values of asymmetry almost in two times!!!. | ||
| − | + | :We need to count isotropic and anisotropic neutrons to estimate the effect of washing out the anisotropy by isotropic neutrons. | |
Revision as of 01:14, 27 June 2011
Motivation: there are a lot of source of isotropic neutrons=
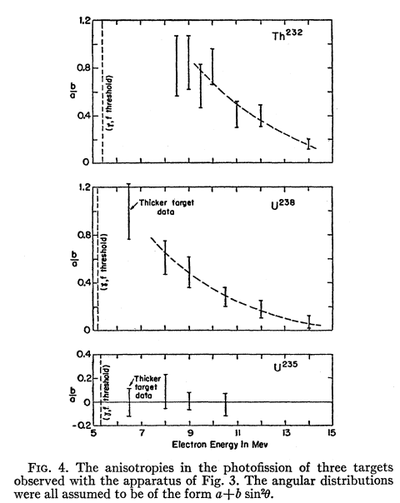
1. Winhold and Halpern, Phys.Rev. 103 4, 990 (1956).
- The observation were consistent with the assumption that
- anisotropic fission is due solely to photons with-in about
- 3 MeV of the fission threshold".
- The photons in the giant resonance region were found
- to produce essentially isotropic fission
2. A lot of other papers.
3. Isotropic neutrons from (,n) channel and (,2n) channel
Anisotropic n's vs. isotropic ones
Say, we have only anisotropic neutrons with 1.25 calculated ratio:
The calculated asymmetry would be:
Now, say, we have extra 100 isotropic neutrons for each detector:
The total number of neutrons become:
So the calculated asymmetry would be:
- So if we would have about the same number of isotropic and anisotropic neutrons that would be reduced the expectation values of asymmetry almost in two times!!!.
- We need to count isotropic and anisotropic neutrons to estimate the effect of washing out the anisotropy by isotropic neutrons.
Source of anisotropic neutrons:
- (,f) channel due to photons with-in about 3 MeV of the fission threshold
Source of isotropic neutrons:
- (,f) channel due to photons out of 3 MeV of the fission threshold
- (,n) channel.
- (,2n) channel.
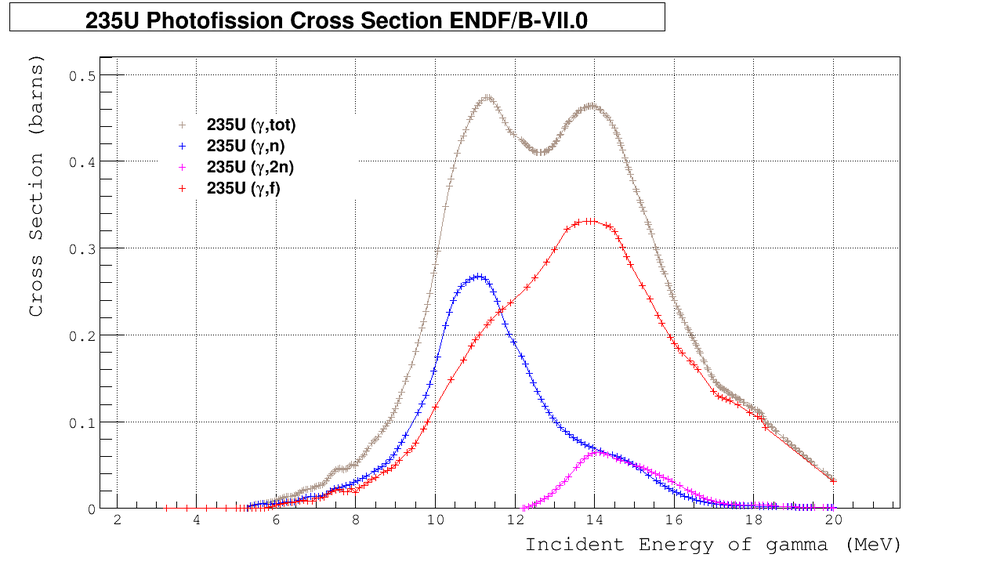
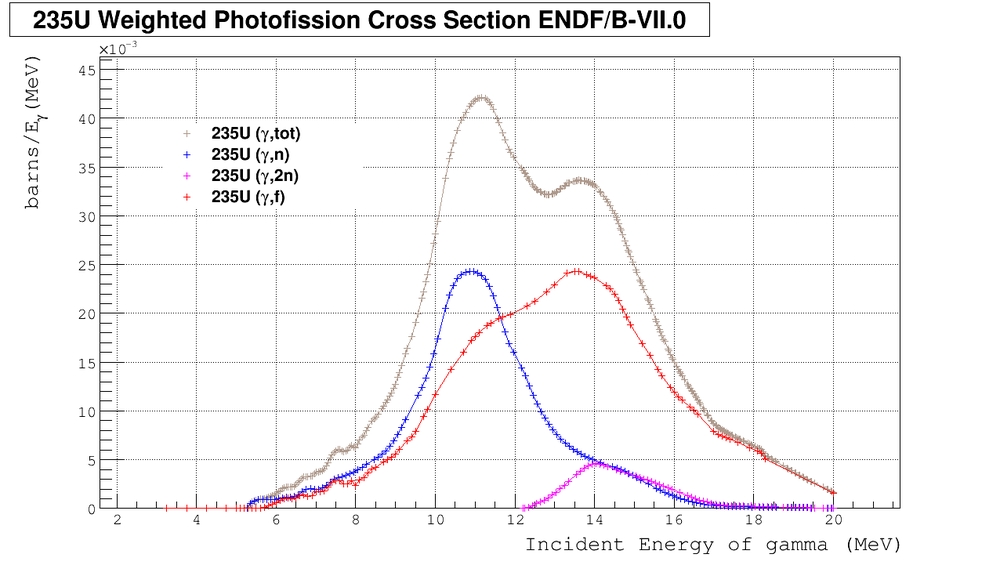
U Photo-fission Cross Section
Let's count isotropic and anisotropic neutrons
Assume most conservative:
Source of anisotropic neutrons:
- (,f) channel for all incident gammas. In reality the number of anisotropic neutrons will reduce with increasing the energy of gammas.
Source of isotropic neutrons:
- (,n) channel
- (,2n) channel
We can calculate the relative number of neutrons from different channels using formulas:
Using root to approximate sigma's by appropriate polynomials and using Maple to estimate integrals I found: