Difference between revisions of "Anisotropic n's vs. isotropic ones"
Jump to navigation
Jump to search
| Line 3: | Line 3: | ||
| − | ==Motivation: Winhold and Halpern, Phys.Rev. 103 4, 990 (1956) | + | ==Motivation: there are a lot of source of isotropic neutrons=== |
| + | |||
| + | #Winhold and Halpern, Phys.Rev. 103 4, 990 (1956). | ||
:'''The observation were consistent with the assumption that''' | :'''The observation were consistent with the assumption that''' | ||
| Line 15: | Line 17: | ||
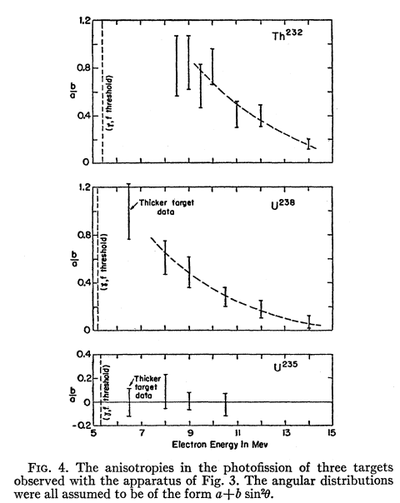
[[File:Winhold fig.4.png | 400px]] | [[File:Winhold fig.4.png | 400px]] | ||
| + | |||
| + | |||
| + | # A lot of other papers. | ||
| + | |||
| + | # Isotropic neutrons from (<math>\gamma</math>,n) channel and (<math>\gamma</math>,2n) channel | ||
==Anisotropic n's vs. isotropic ones== | ==Anisotropic n's vs. isotropic ones== | ||
Revision as of 20:50, 26 June 2011
Motivation: there are a lot of source of isotropic neutrons=
- Winhold and Halpern, Phys.Rev. 103 4, 990 (1956).
- The observation were consistent with the assumption that
- anisotropic fission is due solely to photons with-in about
- 3 MeV of the fission threshold".
- The photons in the giant resonance region were found
- to produce essentially isotropic fission
- A lot of other papers.
- Isotropic neutrons from (,n) channel and (,2n) channel
Anisotropic n's vs. isotropic ones
Say, we have only anisotropic neutrons
So the calculated asymmetry would be:
Now, say, we have extra 200 isotropic neutrons
So the calculated asymmetry would be:
That really reduce the measured asymmetry. If isotropic neutron's are much more than anisotropic ones we would not be able probably to see any asymmetry. Need to count isotropic and anisotropic neutrons.
Source of anisotropic neutrons:
- (,f) channel due to photons with-in about 3 MeV of the fission threshold
Source of isotropic neutrons:
- (,f) channel due to photons out of 3 MeV of the fission threshold
- (,n) channel.
- (,2n) channel.
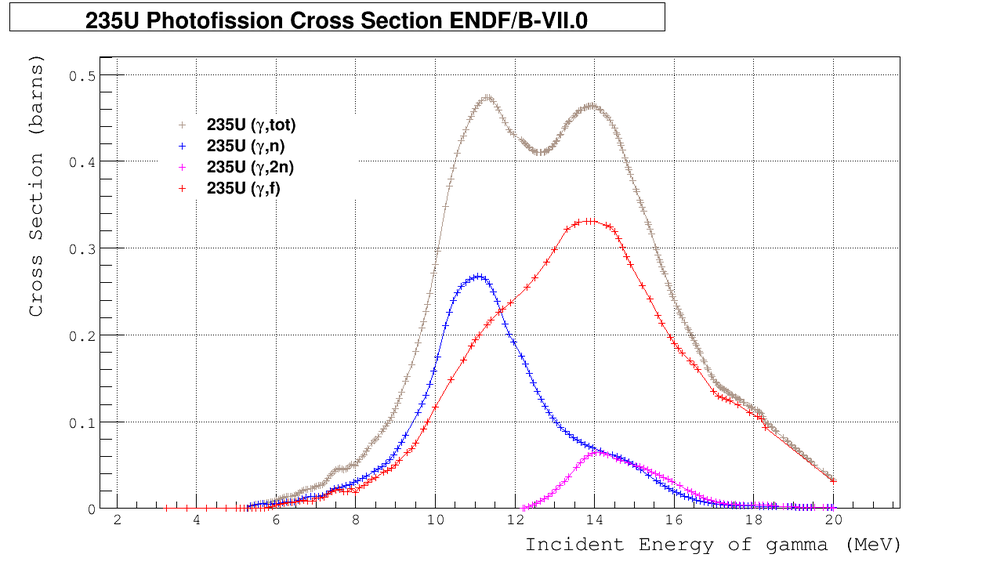
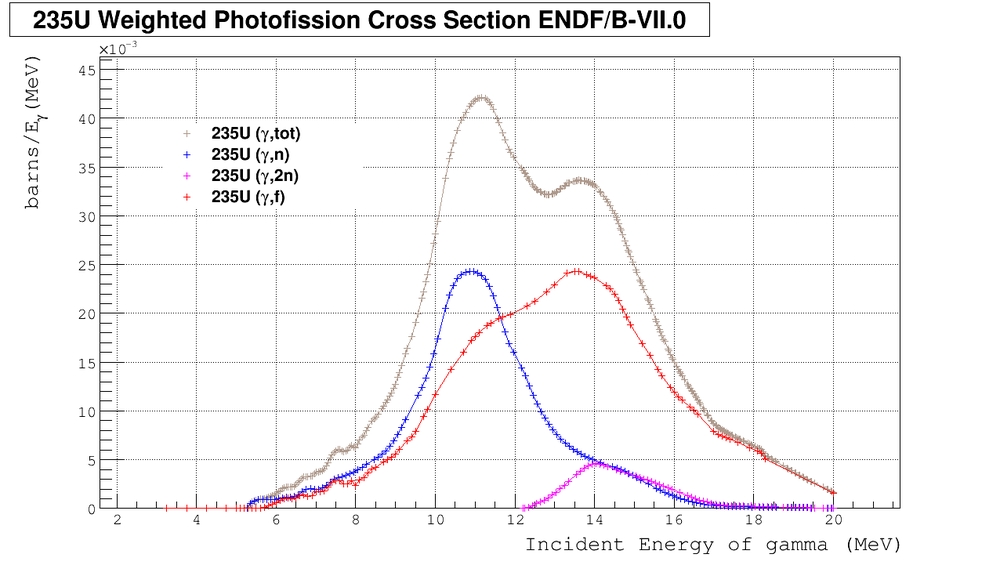
U Photo-fission Cross Section
Let's count isotropic and anisotropic neutrons
Assume most conservative:
Source of anisotropic neutrons:
- (,f). In reality the number of anisotropic neutrons will reduce with increasing the energy of gammas.
Source of isotropic neutrons:
- (,n) channel
- (,2n) channel
We can calculate the relative number of neutrons from different channels using formulas:
Using root to approximate the sigma by appropriate polynomials and using Maple to estimate integrals I found: